Ein billiger Nachbau einer Kopie eines BOSS Blues Drivers – die Schaltung des BOSS' und der Nachbauten wird analysiert. Geiz ist geil & Neugier ist billig – ein neues Spielzeug. Chinesen und lateinische Schriftzeichen. Ran an den Speck. Das erste Vorbild, clevere Wintätsch-OPVs und eine starre Basspumpe. Eine verbesserte Kopie und ein Abschluss mit Siegerehrung.
CGIANT Warm Blues
Kapitelinhalt:[ Überspringen ]Die Vorgeschichte
Anfang der „zehner Jahre“ erwarb der Autor, infolge des wiederentdeckten Interesses für den Klang der E-Gitarre, ein billiges chinesisches Effektgerät, den CGIANT Warm Blues, vertrieben unter dem etwas sonderbaren denglischen Label „Golden Tone“.
Das Angebot an Bodeneffekten umfasste mehrere Geräte – den Nachbau eines Delays des Herstellers BOSS, den Nachbau des bekannten Verzerrers DS-1 des gleichen Herstellers sowie den genannten Overdrive „Warm Blues“, bei dem das Vorbild nicht sofort deutlich war.
Die beiden anderen Geräte wurden im Forum des Händlers „Musikding“ anhand von Fotografien „analytisch auseinandergenommen“. Bei allen Geräten war der Gerätename über Kopf aufgedruckt, was für Erheiterung und skeptische Bemerkungen sorgte, ansonsten überwog das Interesse.
Gerät und Fertigungsqualität
Nun also zum vorliegenden Gerät, einem CGIANT Warm Blues, höchstwahrscheinlich eine Kopie nicht des BOSS Blues Drivers, sondern des Digitech Screamin' Blues. (Der Autor konnte bei der Untersuchung des Gerätes natürlich nicht jeden Widerstand nachsehen, und bei Kondensatoren in SMD hilft selbst ein Fadenzähler nicht weiter.)
Der äußere erste Eindruck ist ernüchternd, nicht nur, dass der Hebel des Fußschalters klappert und die Potentiometerknöpfe wacklig und billig wirken, der Name auch dieses Gerätes ist verkehrt herum auf die Klappe des Fußschalters aufgedruckt – man hat das auf den Werbebildern mit viel Photoshop und etwas zu wenig perspektivischem Denken zu korrigieren versucht.
Das Gerät ist, wie gesagt, in SMD gefertigt, wahrscheinlich zu großen Teilen automatisiert. Die Fertigungsqualität ist durchwachsen, die FETs in den diskreten Operationsverstärkern (bei denen es von der Schaltung her naheliegt, dass sie selektiert wurden) sind mehr schief als schräg auf die Platine aufgeklebt und, so wie es aussieht, von Hand verlötet.
Ansonsten, ein stabiles Stahlgehäuse und alle elektronischen Teile in einem Stück, das heißt, Buchsen und Potentiometer sind fest auf der Platine verlötet. Das bedeutet, alle mechanischen Belastungen von Buchsen und Potentiometer – falls einmal jemand das Gerät versehentlich fallen lässt, betrunken drüber stolpert oder aus Bosheit drauftritt – gehen direkt mit auf die Platine. Auch der eigentliche Taster, mit dem man das Gerät über den Fußschalter aktiviert, ist die Platine gelötet. Den Gummistempel, der auf den Taster drückt, wurde vom Autor gekürzt und neu eingesetzt, weil er ansonsten schon recht früh zuerst auf den Taster und dann auf die Platine drückt.
Die Dokumentation des Gerätes ist lausig, die beiden unterschiedlichen Ausgänge (ein „normaler“ und ein frequenzkorrigierter Ausgang) sind nicht bezeichnet, das muss sich dann wohl selber dranschreiben.
Zur Schaltung
Kapitelinhalt:[ Überspringen ]Da sowohl das gekaufte Gerät (CGIANT Warm Blues) als auch die Vorlage (Digitech Screamin' Blues) erkennbar erweiterte Kopien des BOSS Blues Drivers sind, wird das Grundkonzept der Schaltung anhand des wirklichen Originals beschrieben. Beim Erstellen der Schaltplanzeichnungen musste auf einen schlechten Scan eines von BOSS mitgelieferten Schaltplans (siehe z. B. auf der entsprechenden Seite der Schaltplansammlung freeinfosociety) zurückgegriffen werden. Die beiden Pufferverstärker an Ein- und Ausgang sowie die Umschaltung zwischen Effekt und Bypass wurden nicht gezeichnet; sie sind in den meisten BOSS-Effekten ähnlich und weitestgehend klangneutral (oder sollten es sein.)
Aufgrund der schlechten Qualität des o. g. Scans sind die Angaben zu Größe und Nummerierung der Bauelemente nicht sicher – die Schaltpläne sind also für einen Nachbau nicht geeignet. Letzteres gilt natürlich auch für die Schaltpläne, die der Autor für diese Seite selbst erstellt hat und die hier im Folgenden verwendet werden.
BOSS Blues Driver
Kapitelinhalt:[ Überspringen ]- Ein diskreter Operationsverstärker – statische Kennlinie •
- Ein diskreter Operationsverstärker – dynamisches Verhalten •
- Anwendung der diskreten Operationsverstärker •
- Die Filterschaltung
Schon die Schaltung des BOSS Blues Driver ist für einen Verzerrer etwas ungewöhnlich – die folgenden Schaltpläne Abbildung 1a und Abbildung 1b zeigen die eigentliche „Zerrschaltung“:
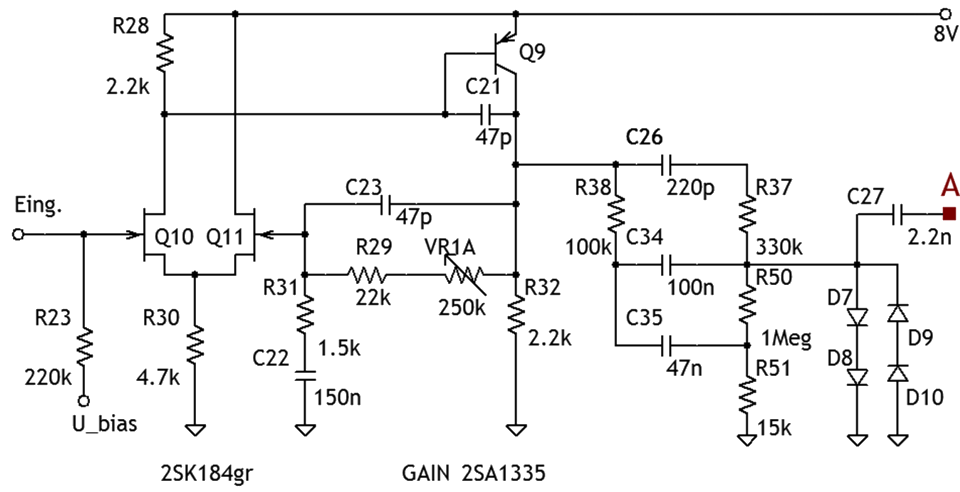

Abb. 1a: Schaltung des esten diskreten Operationsverstärkers, des zwischengeschalteten Tonestacks und der Begrenzerdioden des BOSS Blues Driver.


Abb. 1b: Schaltung des zweiten Operationsverstärkers im BOSS Blues Driver.
Ein diskreter Operationsverstärker – statische Kennlinie
Die Verzerrung entsteht im Wesentlichen durch Übersteuerung von zwei diskreten Operationsverstärkern, bestehend aus einem als Differenzverstärker beschalteten FET-Pärchen (Q10 und Q11 bzw. Q14 und Q13) und einem als Ausgangstreiber genutzten bipolaren Transistor (Q9 bzw. Q12), wobei durch letzteren bei hohem Ausgangspegel die untere Halbwelle des Ausgangssignals sanft und die andere hart begrenzt wird (asymmetrisch hartes / weiches Clipping).
Diese diskreten Operationsverstärker und ihr Übersteuerungsverhalten verdienen eine eingehendere Betrachtung, was im Folgenden anhand einer Berechnung derg Verstärkung sowie einer mathematischer Betrachtung von Frequenz- und Phasengang geschehen soll.
Begonnen wird dazu am linken JFET des ersten diskreten Operationsverstärkers – hier wird das Eingangssignal zunächst zwischen den Gate-Source-Strecken der beiden JFET-Transistoren „aufgeteilt“ und führt anschließend zu einem Signalstrom am Drain von Q10:
\( \begin{equation} i_{\textrm{D,10}} = u_{\textrm{GS,10}}\cdot{}S_{\textrm{Q10,AP}} \tag{1}\end{equation} \)
Signalmäßig betrachtet bilden die reziproken Steilheiten von Q10 und Q11 sowie der Sourcewiderstand R30 einen Spannungsteiler für das Differenzeingangssignal:
\( \begin{eqnarray} \frac{u_{\textrm{GS,10}}} {u_{\textrm{G,10}}-u_{\textrm{G,11}}} & = & \frac{\cfrac{1} {S_{\textrm{Q10,AP}}}} {\cfrac{1} {S_{\textrm{Q10,AP}}} + \left( \cfrac{1} {S_{\textrm{Q11,AP}}} || R_{\textrm{30}} \right) } \\~\\ & = & \frac{\cfrac{1} {S_{\textrm{Q10,AP}}}} {\cfrac{1} {S_{\textrm{Q10,AP}}} + \cfrac{1} {S_{\textrm{Q11,AP}}} \left( 1||\! \left[ R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}} \right] \right) } \\~\\ & = & \frac{\cfrac{1} {S_{\textrm{Q10,AP}}} } {\cfrac{1} {S_{\textrm{Q10,AP}}} +\cfrac{1} {S_{\textrm{Q11,AP}}} \left( \cfrac{R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} {1+R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} \right) } \tag{2}\end{eqnarray} \)
Nach dem Erweitern beider Seiten der Gleichung mit uG,10−uG,11 und mit SQ10,AP sowie unter Einbeziehung von Gleichung 1 lässt sich schreiben:
\( \begin{eqnarray} i_{\textrm{DS,10}} & = & \frac{u_{\textrm{G,10}}-u_{\textrm{G,11}}} { \cfrac{1} {S_{\textrm{Q10,AP}}} + \cfrac{1} {S_{\textrm{Q11,AP}} } \left( \cfrac{R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} {1+R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} \right) } \tag{3}\end{eqnarray} \)
Ausgehend davon lässt sich für den Differenzverstärker (bzw. für dessen lineares Kleinsignalverhalten um den Arbeitspunkt) eine Gesamtsteilheit Sdiff ermitteln, die sich ergibt als Quotient aus der Änderung des Drainstroms durch R28 und der Änderung des Differenzeingangsspannung uG,10 – uG,11:
\( \begin{eqnarray} S_{\textrm{diff}} & = & \frac{i_{\textrm{DS,10}}} {u_{\textrm{G,10}}-u_{\textrm{G,11}}} \\ & = & \frac{1} { \cfrac{1} {S_{\textrm{Q10,AP}}} + \cfrac{1} {S_{\textrm{Q11,AP}}} \left(\cfrac{R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} {1+R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} \right) } \tag{4}\end{eqnarray} \)
Die Steilheit S eines JFET hängt natürlich von dessen Daten (hier UGS,0 und IDSS) wie auch von dessen Sourcestrom ab. Wenn man davon ausgeht, dass Q10 und Q11 paarig selektiert wurden (der innere Aufbau des dem Autor vorliegenden Gerätes CGIANT Warm Blues legt das zumindest nahe – die JFET-Transistoren wurden von Hand eingelötet), kann man für beide JFET-Transistoren von den gleichen Daten ausgehen. Unter Umständen unterscheiden sich die JFET-Transistoren aber möglicherweise in ihrem Sourcestrom.
Die Summe beider Sourceströme wird durch Sourcespannung (größer 4 V) und durch den gemeinsamen Sourcewiderstand R30 bestimmt; sie liegt bei etwa 1 mA.
Der Source- bzw. Drainstrom von Q10 wird am stärksten durch die Größe von R28 und die Tatsache bestimmt, dass zwischen Basis und Emitter von Q9 etwa 0,6 V bis 0,7 V anliegen – Q10 hat also einen Drainstrom von etwa 0,3 mA und demzufolge Q11 einen von etwa 0,7 mA. Der Basisstrom von Q9 ist dagegen sehr klein, er liegt nur bei einigen Mikroampere und fällt hier nicht ins Gewicht.
Das Datenblatt des verwendeten JFET 2SK184 (siehe die folgende Abbildung 2) legt für einen Sourcestrom von 0,3 mA eine Steilheit von etwa 6 mS und für einen Sourcestrom von 0,7 mA eine Steilheit von etwa 8 mS nahe.
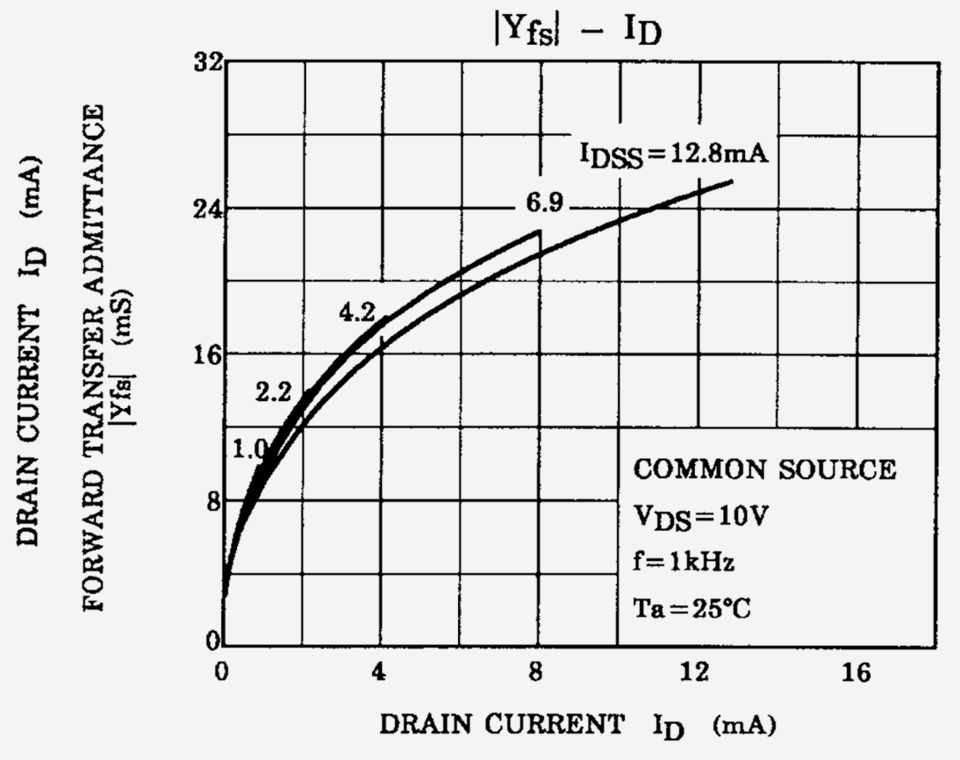

Abb. 2: Steilheit des JFET 2SK184 in Abhängigkeit vom Sourcestrom – Auszug aus dem Datenblatt des Herstellers.
Diese Werte können nun in obige Gleichung 4 eingesetzt werden. Dabei ergibt sich beim Vergleich der Werte von R30 und der Steilheit von Q11 eine weitere mögliche Vereinfachung – dadurch, dass der gemeinsame Sourcewiderstand R30 wesentlich größer ist als die reziproke Steilheit des zweiten JFET Q11, kann R30 hier vernachlässigt werden und der zusätzliche Bruch im Nenner der Gleichung entfallen. Die Vereinfachungen betreffen eben den eingeklammerten Bruch in Nenner der rechten Seite:
\( \begin{eqnarray} \frac{R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} {1+R_{\textrm{30}}\cdot{}S_{\textrm{Q11,AP}}} & = & \frac{4{,}7\,\textrm{kΩ}\cdot{}8\,\textrm{mS}} {1+4{,}7\,\textrm{kΩ}\cdot{}8\,\textrm{mS}} = \frac{37{,}6} {1+37{,}6} \\~\\ & \approx{} & 1 \tag{5}\end{eqnarray} \)
Für SQ10,AP = 8 mS und R30 = 4,7 kΩ ergibt sich jetzt aus der vereinfachten Gleichung 4 mit ausreichender Genauigkeit:
\( \begin{eqnarray} S_{\textrm{diff}} & \approx & \frac{1} { \cfrac{1}{S_{\textrm{Q10,AP}}} + \cfrac{1}{S_{\textrm{Q11,AP}}} } = \frac{1} { \cfrac{1} {6\,\textrm{mS}} + \cfrac{1} {8\,\textrm{mS}} } \\~\\ & \approx & 3{,}4\,\textrm{mS} \tag{6}\end{eqnarray} \)
Das Differenzeingangssignal der beiden Gates führt also mit einer Steilheit von etwa 3,4 mS zu einem Signalstrom an Q10.
Dieser Signalstrom teilt sich dann am Stromteiler, bestehend aus dem Drainwiderstand R28 und der Basis-Emitter-Strecke von Q9, auf. Um den differentiellen Widerstand dieser Basis-Emitter-Strecke berechnen oder wenigstens abschätzen zu können, muss der Arbeitspunkt von Q9 betrachtet werden:
Im Ruhezustand bzw. im Arbeitspunkt des diskreten Operationsverstärkers haben dessen Ausgang und dessen invertierender Eingang, d. h. das Gate von Q11 wie auch der Kollektor von Q9, dieselbe Spannung wie dessen Eingang, das Gate von Q10 – etwa die halbe Betriebsspannung. (Es wird vernachlässigt, dass sich die Gate-Source-Spannungen von Q10 und Q11 aufgrund der unterschiedlichen Sourceströme geringfügig unterscheiden.) Die Spannung UR32 über dem Kollektorwiderstand R32 beträgt dann ebenfalls etwa 4 V und der Kollektorstrom von Q9 hat einen Wert von 1,8 mA.
Für den Basisruhestrom von Q9 gilt dann:
\( \begin{equation} I_{\textrm{B,9}} = \cfrac{U_{\textrm{R32}}} {R_{\textrm{32}}\cdot{}\beta_{\textrm{Q9}}} \tag{7}\end{equation} \)
Der differentielle Widerstand der Basis-Emitter-Strecke von Q9 leitet sich nun entsprechend der Shockley-Gleichung grob aus dem Stromverstärkungsfaktor des Transistors, der Größe des Basisstroms, der sogenannten Temperaturspannung UT (26 mV) und dem materialabhängigen Emissionskoeffizienten η (bei Silizium etwa 1,7) ab:
\( \begin{eqnarray} r_{\textrm{BE,9}} & = & \eta\cdot{} \frac{U_{\textrm{T}}} {i_{\textrm{B,9}}} \\~\\ & = & \beta_{\textrm{Q9}}\cdot{} \frac{ \eta\cdot{} U_{\textrm{T}}\cdot{} R_{\textrm{32}} } {U_{\textrm{R32}}} \tag{8}\end{eqnarray} \)
Einen Stromverstärkungsfaktor von Q9 von beispielsweise 300 angenommen, ergibt sich für Q9 im Arbeitspunkt ein differenzieller Basis-Emitter-Widerstand von etwa 7 kΩ; d. h. signalmäßig betrachtet wird die Basis-Emitter-Strecke von Q9 durch R28 zum Teil kurzgeschlossen.
Für den Signalstrom an der Basis von Q9 in Abhängigkeit von der Eingangsspannung des JFET-Differenzverstärkers lässt sich jetzt unter Anwendung der Stromteilerregel an rBE,9 und R28 zusammenfassen:
\( \begin{eqnarray} i_{\textrm{B,9}} & = & \frac{R_{\textrm{28}}} {r_{\textrm{BE,9}}+R_{\textrm{28}}} \cdot\Delta u_{\textrm{e}} \cdot{} S_{\textrm{diff}} \\~\\ & = & \frac{R_{\textrm{28}}} {\beta_{\textrm{Q9}} \cdot\cfrac{\eta\cdot{}U_{\textrm{T}}} {I_{\textrm{C,2}}} + R_{\textrm{28}} } \cdot{} \Delta u_{\textrm{e}} \cdot{} S_{\textrm{diff}} \\~\\ & = & \frac{1} {\beta_{\textrm{Q9}} \cdot{}\cfrac{\eta\cdot{} U_{\textrm{T}}\cdot{}R_{\textrm{32}} } { U_{\textrm{R32}}\cdot R_{\textrm{28}}} + 1 } \cdot{} \Delta u_{\textrm{e}} \cdot{} S_{\textrm{diff}} \tag{9}\end{eqnarray} \)
Für den Kollektorsignalstrom von Q9 ergibt sich dann:
\( \begin{eqnarray} i_{\textrm{C,9}} & = & \beta_{\textrm{Q9}}\cdot \frac{R_{\textrm{28}}} { \beta_{\textrm{Q9}}\cdot \cfrac{\eta\cdot U_{\textrm{T}}\cdot R_{\textrm{32}} } {U_{\textrm{R32}}} + R_{\textrm{28}} } \cdot\Delta u_{\textrm{e}} \cdot{} S_{\textrm{diff}} \tag{10}\end{eqnarray} \)
Da – in der konkreten Schaltung – die Werte von R28 und R32 gleich sind, lässt sich hier kürzen:
\( \begin{eqnarray} i_{\textrm{C,9}} & = & \frac{1} { \cfrac{\eta\cdot{}U_{\textrm{T}}} {U_{\textrm{R32}}} + \cfrac{1} {\beta_{\textrm{Q9}}} } \cdot{} \Delta u_{\textrm{e}} \cdot{} S_{\textrm{diff}}\\ \tag{11}\end{eqnarray} \)
und daraus für die Leerlaufverstärkung dieses diskreten Operationsverstärkers im Arbeitspunkt ableiten:
\( \begin{eqnarray} V_{\textrm{U,AP}} & = & \frac{R_{\textrm{32}}\cdot i_{\textrm{C,9}}} {\Delta u_{\textrm{e}}} \\ & = & R_{\textrm{32}}\cdot{} S_{\textrm{diff}}\cdot{} \frac{1} { \cfrac{\eta\cdot{}U_{\textrm{T}}} {U_{\textrm{R32}}} + \cfrac{1} {\beta_{\textrm{Q9}}} } \\ & = & \frac{7{,}5} { \cfrac{44\,\textrm{mV}} {U_{\textrm{R32}}} + \cfrac{1}{300} } \tag{12}\end{eqnarray} \)
Dass hier die Ausgangsspannung (nicht die Signalspannung am Ausgang, sondern die Spannung vom Ausgang gegen Masse UR32) in der Formel zur Berechnung der Leerlaufverstärkung des diskreten Operationsverstärkers auftaucht, weist auf eine nichtlineare Kennlinie hin – bei einer linearen Kennlinie hätte der Verstärkungsfaktor von sich verändernden Größen möglichst unabhängig zu sein. Dabei ist BOSS mit dieser Schaltung eines diskreten Operationsverstärkers ein Bauelement mit einer interessant nichtlinearen (etwa quadratischen) Kennlinie gelungen. Bei diesem diskreten Operationsverstärkers hängt der Quotient der Änderung von Ausgangs- zu Eingangsspannung dUa / dUe fast linear vom augenblicklichen Wert der Ausgangsspannung ab – solange das Verhältnis der Ausgangsspannung (d. h. die Spannung über R32) zum Produkt UT ⋅ η wesentlich kleiner ist als der Stromverstärkungsfaktor des Transistors Q9, steigt oder sinkt die Verstärkung mit der Ausgangsspannung – diese wird aber letztendlich durch die Größe des Stromverstärkungsfaktors von Q9 begrenzt.
Das bedeutet, dass der Operationsverstärker mit einer eher gekrümmten Kennlinie und einer asymmetrischen Begrenzung arbeitet; in der unteren Halbwelle ist die Verstärkung geringer, die untere Halbwelle des diskreten Operationsverstärkers wird weich begrenzt, wohingegen die obere Halbwelle hart unter der Betriebsspannung abgeschnitten wird.
Abgesehen davon hat dieser diskrete Operationsverstärker im Gegensatz zu integrierten Operationsverstärker einen relativ großen Headroom und ist so sehr gut an die relativ geringe Betriebsspannung in Bodeneffektgeräten angepasst.
Mit PSPICE wurde die Schaltung des diskreten Operationsverstärkers noch einmal in Hinblick auf dessen statische Kennlinie modelliert, wobei allerdings keine passende Modelle für die in der Originalschaltung benutzten Transistoren zur Verfügung standen – es handelt sich als nur um ein qualitatives Modell. Abbildung 3 zeigt die Schaltung der Simulation:
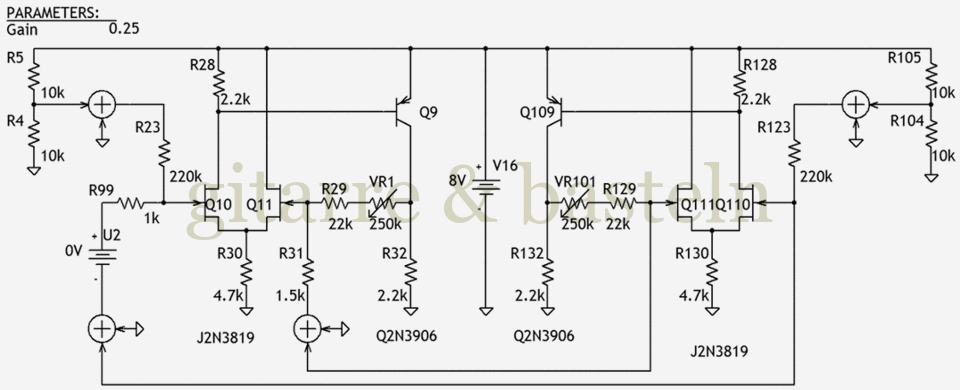

Abb. 3: Simulationsschaltung zur qualitativen Ermittlung der statischen Kennlinie eines diskreten Operationsverstärkers wie z. B. im BOSS Blues Driver – bei der Simulation wurden andere Transistor(modelle) verwendet.
Die rechte Hälfte der Schaltung dient der Ermittlung der Arbeitspunkte am Gate des ersten JFET und am Fußpunkt der Gegenkopplung. Das Diagramm der statischen Kennlinie beschreibt, bei welcher Eingangsspannung (Gate von Q10) welche Ausgangsspannung (Kollektor von Q10) zu erwarten ist. Die folgende Abbildung 4 zeigt die statische Kennlinie der simulierten Schaltung nach Abbildung 3:
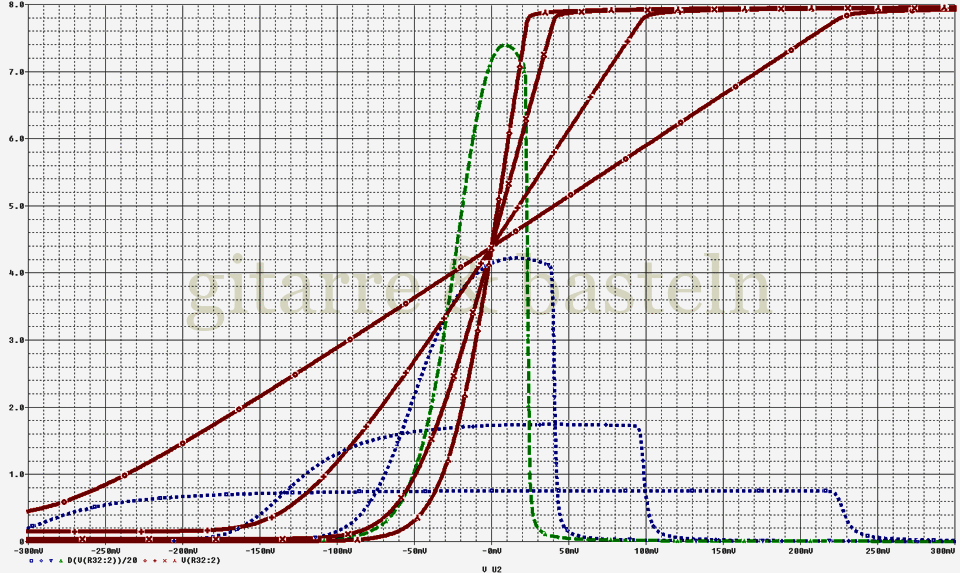

Abb. 4: Statische Kennlinie eines simulierten diskreten Operationsverstärkers wie in Abbildung 3. Die Kennlinie wurde simuliert für einen Gain-Regler auf „0“, „0,16“ und „1“ sowie bei quasi entfernter Gegenkopplung (Gain = 100). Die gepunkteten Linien zeigen den entsprechenden Verstärkungsfaktor, dividiert durch 20.
Die unterschiedlich scharfe Begrenzung an den beiden Aussteuerungsgrenzen ist deutlich zu sehen.
Das beschriebene nichtlineare Verhalten wird natürlich notwendigerweise durch die zugeschaltete Gegenkopplung linearisiert – d. h. der diskrete Operationsverstärkers klippt in der unteren Halbwelle weniger weich und verhält sich stärker linear, wenn die Verstärkung durch einen zurückgedrehten Gain-Regler stärker reduziert wurde. Auch das ist im Kennliniendiagramm in Abbildung 4 deutlich zu erkennen (je größer der Aussteuerungsbereich d. h. je kleiner die Verstärkung, desto gerader bzw. linearer die Kennlinie).
Um die quantitative und auch die qualitative Wirkung der Gegenkopplung einschätzen zu können, muss die Leerlaufverstärkung des diskreten Operationsverstärkers zumindest grob quantitativ bestimmt werden. Zunächst soll das Verhalten bei kleinen Signalen betrachtet werden. Unter den gegebenen Bedingungen (UR32 etwa 4 V, β etwa gleich dreihundert) kann man für kleine Signale bzw. das Verhalten im Arbeitspunkt ableiten:
\( \begin{eqnarray} V_{\textrm{U,AP}} & = & \frac{7{,}5} { \cfrac{44\,\textrm{mV}} {4\,\textrm{V}} + \cfrac{1} {300} } \approx{} 500. \tag{13}\end{eqnarray} \)
Für die positive Halbwelle steigt die maximale Verstärkung bis auf etwa 850. Die maximale Gegenkopplung liegt etwa im Bereich größer hundert.
Bei einer absoluten Ausgangsspannung UR32 von etwa 500 mV gegen Masse (d. h. im Ende der unteren Halbwelle) sinkt die Leerlaufverstärkung des diskreten Operationsverstärkers ebenfalls auf etwa einhundert, bei einer absoluten Ausgangsspannung von etwa 1 V auf etwa einhundertfünfzig. Das bedeutet, dass die untere Halbwelle des Signals (im Bereich etwa ein Volt „über null“) weich geklippt wird, sofern der Gain-Regler aufgedreht worden ist.
Ein diskreter Operationsverstärker – dynamisches Verhalten
Soweit zum statischen Verhalten bzw. zur statischen Kennlinie des von BOSS entwickelten diskreten Operationsverstärkers, interessant ist jedoch auch das zu einem „normalen“ Operationsverstärker unterschiedliche dynamische Verhalten, d. h. Frequenz- und Phasengang des nicht gegengekoppelten Verstärkers und, daraus folgend, das Verhalten bei Übersteuerung.
Ein „normaler“ integrierter Operationsverstärker hat seine sehr hohe Leerlaufverstärkung nur bei sehr kleinen Frequenzen, diese fällt (üblicherweise über den gesamten Tonfrequenzbereich) mit 20 dB / Dekade bis zur sogenannten Transitfrequenz – die Verstärkung bei der Transitfrequenz ist eins. Damit einher geht (ebenfalls über den gesamten Tonfrequenzbereich) eine Phasenverzögerung von fast 90°.
Das ist, solange der Operationsverstärker im linearen Bereich arbeitet, nicht unbedingt ein Problem – hier wird dessen Ausgangssignal im Wesentlichen über die Gegenkopplung bestimmt. Der Operationsverstärker arbeitet hier – mit einer Phasenverzögerung von 90°, d. h. mit einer gewissen Behäbigkeit – als Regler, der versucht, das Ausgangssignal fortlaufend so einzustellen, dass die Eingangsspannung am invertierenden Eingang mit der amg nichtinvertierenden Eingang übereinstimmt. Ist der Operationsverstärker beispielsweise mit einem Spannungsteiler eins zu zehn gegengekoppelt, wird sein Ausgangssignal zehnmal so groß sein wie sein Eingangssignal.
Bei Übersteuerung gerät diese Arrangement natürlich durcheinander, der Operationsverstärker wird bei einem zu großen Eingangsimpuls erst einmal „gegen die Wand laufen“, d. h. an seine Aussteuerungsgrenzen kommen, ehe die Gegenkopplung wieder einsetzen und das Verhalten der gesamten Schaltung kontrollieren kann, was dann u. U. zu merkwürdigen Verhalten, z. B. zu einer Art „Panikreaktion“ wie Überschwingen am Ausgang führen kann.
Nun stellt sich natürlich die Frage, ob das bei dem hier verwendeten diskreten Operationsverstärker auch so ist. Um das beurteilen zu können, müssen Frequenz- und Phasengang dieses diskreten Operationsverstärkers untersucht werden.
In dessen Schaltung (siehe Abbildung 1a; im Folgenden geht es der Einfachheit halber nur um den ersten Operationsverstärker) findet sich genau ein frequenzabhängiges Bauelement – der Kondensator C21 (47 pF) zwischen Basis und Kollektor des bipolaren Ausgangstransistors Q9 – der dann auch ein Tiefpassverhalten des gesamten diskreten Operationsverstärkers bewirkt. C21 wird hier zu einer sogenannten Miller-Kapazität, d. h. die Kapazität, mit der sich an C21 und dem Drainwiderstand von Q10, R28, ein Tiefpassverhalten realisiert, verstärkt sich proportional zur (negativen) Verstärkung von Q9. Das bedeutet, dass die Frequenz des Tiefpasses, der an der Basis von Q9 entsteht, davon abhängt, wie sehr Q9 das Signal verstärkt.
Wie hängt das alles zusammen? Weiter oben wurde ausgeführt, dass das Differenzsignal zwischen den Gates der beiden JFET-Transistoren, Q10 und Q11, zu einem Signalstrom am Drain des linken JFET Q10 führt. Dieser Signalstrom wird, der Stromteilerregel folgend, zwischen dem Drainwiderstand R28 und dem differentiellen Basis-Emitter-Widerstand des bipolaren Transistors Q9 aufgeteilt und dann durch letzteren zumg Kollektorstrom und damit zur Ausgangsspannung des diskreten Operationsverstärkers verstärkt.
Dabei entsteht – sozusagen unterwegs – auch am Drain von Q10 eine Signalspannung, da der (Signal-)Drainstrom von Q10 parallel durch dessen Drainwiderstand R28 und durch den differentiellen Basis-Emitter-Widerstand von Q9 fließt. Das heißt, wenn man jetzt zunächst einmal den Kondensator C21 ignoriert, kann man schreiben:
\( \begin{equation} u_{\textrm{D,10}}=i_{\textrm{D,10}}\cdot{} \left(R_{\textrm{28}} || r_{\textrm{BE,9}} \right) \tag{14}\end{equation} \)
Diese Spannungsquelle uD,9 hat nun einen Innen- oder Quellwiderstand in Höhe der Parallelschaltung von R28 undg rBE,9. Dieser Innen- oder Quellwiderstand bildet mit der Miller-Kapazität an Q9 einen Tiefpass, dessen Grenzfrequenz jetzt abgeschätzt werden soll:
\( \begin{eqnarray} f_{\textrm{TP}} &=& \frac{1} {2\pi{}\cdot{} C_{\textrm{Miller}}\cdot{} \left(R_{\textrm{28}} || r_{\textrm{BE,Q9}} \right) } \\~\\ &=& \frac{1} {2\pi{}\cdot{} v_{\textrm{U,Q9}}\cdot{} C_{\textrm{21}}\cdot{} \left(R_{\textrm{28}} || r_{\textrm{BE,Q9}}\right ) } \tag{15}\end{eqnarray} \)
Die Formel für den differentiellen Widerstand rBE,Q9 wurde weiter oben schon einmal abgeleitet,g hier wird erst einmal nur der ungefähre Wert vong rBE,Q9 ermittelt:
\( \begin{eqnarray} r_{\textrm{BE,Q9}} &= & \beta_{\textrm{Q9}}\cdot{} \frac{\eta\cdot{} U_{\textrm{T}}\cdot{} R_{\textrm{32}}} {U_{\textrm{R32}}} \\~\\ & \approx & 300\cdot{} \frac{1{,}7\cdot{} 26\,\textrm{mV}\cdot{} 2{,}2\,\textrm{kΩ}} {\textrm{4 V}} \\~\\ & \approx & 7\,\textrm{kΩ} \tag{16}\end{eqnarray} \)
Damit ergibt sich für die Parallelschaltung von R28 und rBE,Q9 ein Wert von etwa 1,7 kΩ. Der nächste Schritt zur Ermittlung der Tiefpassfrequenz besteht jetzt darin, die Spannungsverstärkung vU,Q9 von der Basis zum Kollektor von Q9 zu ermitteln.
\( \begin{eqnarray} v_{\textrm{U,Q9}} &=& \frac{u_{\textrm{C,Q9}}} {u_{\textrm{B,Q9}}} \\~\\ v_{\textrm{U,Q9}} &=& \frac{i_{\textrm{C,Q9}}\cdot{} R_{\textrm{32}}} {u_{\textrm{B,Q9}}} \\~\\ v_{\textrm{U,Q9}} &=& \frac{i_{\textrm{B,Q9}}\cdot{} \beta_{\textrm{Q9}}\cdot{} R_{\textrm{32}}} {u_{\textrm{B,Q9}}} \\~\\ v_{\textrm{U,Q9}} &=& \frac{u_{\textrm{B,Q9}}} {r_{\textrm{BE,Q9}}} \cdot{} \frac{\beta_{\textrm{Q9}}\cdot{} R_{\textrm{32}}} {u_{\textrm{B,Q9}}} \\~\\ v_{\textrm{U,Q9}} &=& \frac{1} {r_{\textrm{BE,Q9}}} \cdot{} \beta_{\textrm{Q9}}\cdot{} R_{\textrm{32}} \tag{17}\end{eqnarray} \)
An diesem Punkt ist ein Einschub nötig, weiter oben wurde bereits rBE,Q9 aus dem Arbeitspunkt von Q9 abgeleitet:
\( \begin{eqnarray} r_{\textrm{BE,Q9}} &=& \beta_{\textrm{Q9}}\cdot{} \frac{ \eta\cdot{} U_{\textrm{T}}\cdot{} R_{\textrm{32}}} {U_{\textrm{R32}}} \tag{18}\end{eqnarray} \)
Das lässt sich jetzt einsetzen und vereinfachen:
\( \begin{eqnarray} v_{\textrm{U,Q9}} & = & \frac{U_{\textrm{R32}}} {\beta_{\textrm{Q9}}\cdot{} \eta{}\cdot{} U_{\textrm{T}}\cdot{} R_{\textrm{32}}} \cdot{} \beta_{\textrm{Q9}} \cdot{} R_{\textrm{32}} \\~\\ v_{\textrm{U,Q9}} & = & \frac{U_{\textrm{R32}}} {\eta{}\cdot{} U_{\textrm{T}}} \tag{19}\end{eqnarray} \)
Ergebnis ist eine Formel, die durchaus Allgemeingültigkeit besitzt. Sie wird wieder in die Ursprungsgleichung 15 eingesetzt, undg mit dem oben abgeschätzten Wert fürg R28 || rBE,Q9 ergibt sich für fTP:
\( \begin{eqnarray} f_{\textrm{TP}} &=& \frac{\eta{}\cdot{} U_{\textrm{T}}} {U_{\textrm{R32}}} \cdot{} \frac{1} {2\pi{}\cdot{} C_{\textrm{21}}\cdot{} \left(R_{\textrm{28}} || r_{\textrm{BE,Q9}} \right) } \\~\\ &\approx{}& \frac{1{,}7\cdot{}26\,\textrm{mV}} {4\,\textrm{V}} \cdot{} \frac{1} {2\pi{}\cdot{} 47\,\textrm{pF}\cdot{} 1{,}7\,\textrm{kΩ} } \\~\\ f_{\textrm{TP}} &\approx{}& 22\,\textrm{kHz} \tag{20}\end{eqnarray} \)
Das ist ein gutes Ergebnis, es bedeutet, dass bei demg diskrete Operationsverstärker im für Gitarre wesentlichen Audiobereich mit keinen oder kaum wesentlichen Verlusten an Verstärkung oder mit Phasenverschiebungen zu rechnen ist. Eine Operationsverstärker, dessen Verstärkung erst mit dem Ultraschallbereich beginnend sinkt und der auch die Phase erst mit Ultraschallbereich beginnend merklich verzögert, kann im Audiobereich auf Übersteuerungen wesentlich „disziplinierter“ reagieren, d. h. beim Klippen ist ein Entstehen zusätzlicher Peaks oder ein Überschwingen weniger wahrscheinlich als bei einem „klassischen“ bzw. üblichen Operationsverstärker.
Insgesamt kann man von dem BOSS entwickelten diskreten Operationsverstärker wohl durchaus ein musikalisches Übersteuerungsverhalten erwarten.
Anwendung der diskreten Operationsverstärker
Nun zum Einsatz der beiden diskreten Operationsverstärker in der Schaltung des BOSS Blues Drivers, von denen einer tendenziell eher als Booster oder als „diskreter Tubescreamer“ und der andere als eigentliche Zerrstufe eingesetzt wird.
Mit der Gegenkopplung des ersten diskreten Operationsverstärker (in obiger Schaltzeichnung R31 und C22) werden die Bässe und Mitten beginnend bei etwa 700 Hz abgesenkt; im Ausgang dieses Operationsverstärkers wird das Signal hinter einem Filter, dass die Bässe wieder leicht anhebt (C26, C34 und C35 sowie R38—R37, R50 und R51 – ein Fender-typisches „Tonestack“ mit zugedrehten Mitten und Höhen), von zwei mal zwei antiparallelen (Clipping)dioden begrenzt.
Diese Begrenzung kann dabei nicht allzu intensiv sein – siehe dazu die folgende Abbildung 5. Sie zeigt den Frequenzgang des genannten Filters. Würde diesem Filter ein Signal mit einer Amplitude von 3 V (was einer Ausgangsspannung des diskreten Operationsverstärkers von etwa 8 V Spitze-Spitze entspricht) eingespeist, so würde die Ausgangsspannung bei tiefen Frequenzen kaum 1 V und ansonsten kaum oder gerade 500 mV erreichen.
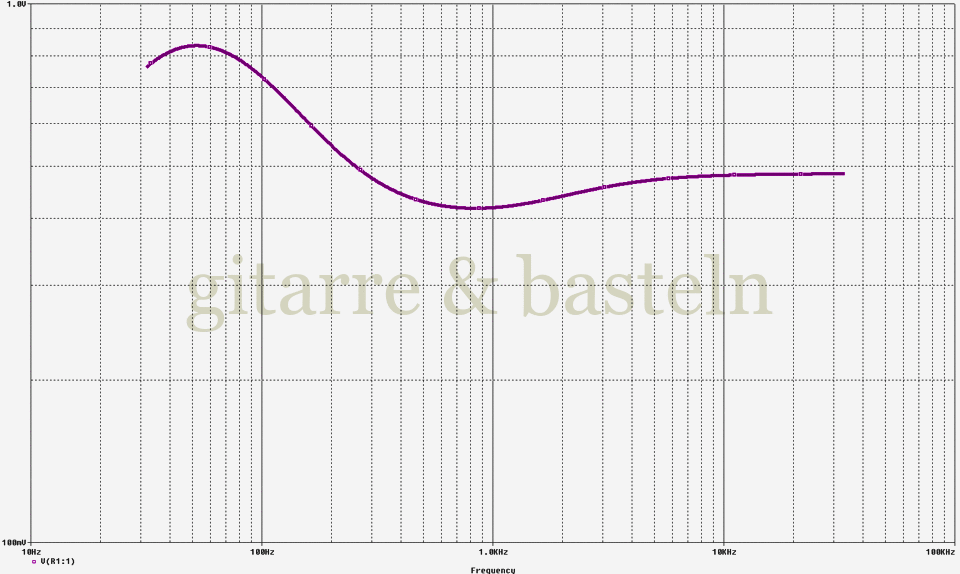

Abb. 5: Frequenzgang des Tonestacks im BOSS Blues Driver. Es wurde am Eingang des Klangfilters ein Signal mit einer Amplitude von 3 V (≈ 8,4 V Spitze-Spitze) eingespeist
Wie ist das zu erklären? Die „linke untere Seite“ des Filters bildet einen Tiefpass 30 Hz bis 220 Hz (R38, C35, R51). Für Frequenzen wesentlich größer als etwa 220 Hz wirkt dieser Tiefpass als Spannungsteiler aus R38 und R51 mit einem Ausgangswiderstand von etwa 13 kΩ (R38 parallel R51). Das Ausgangssignal dieses Spannungsteilers wird von C34 nur durchgelassen; der „aufgedrehte“ Bassregler R50 ist bedeutungslos, weil zu groß und der Höhenregler (die Reihenschaltung von C26 mit R37) wirkt erst bei Frequenzen größer etwa 2 kHz und ist ohnehin „zugedreht“.
Für Frequenzen größer als etwa 200 Hz und bei (momentanen) Spannungsspitzen von maximal ± 4 V am Eingang des Filters treten also bei den Dioden Peaks von etwa 500 mV auf, was bedeutet, dass auf jede der zwei in Serie geschalteten Dioden jeweils maximal 250mV abfallen. Bei dieser Spannung sperren die Dioden noch fast vollständig.
Für tiefere Frequenzen als 200 Hz ist die Dämpfung des genannten Tiefpasses geringer – über C35 und R51 fließt ein kleinerer Signalstrom (ab). Im Extremfall fließt der gesamte Signalstrom durch R38 zu den Begrenzerdioden. Ein Signal von ± 4 V geringer Frequenz am Eingang des Filters würde zu einem Strom durch R38 von etwa 30 µA führen. Bei einem solchen Strom hätten die Begrenzerdioden einen differentiellen Innenwiderstand von zusammen etwa 3 kΩ (2 ⋅ η ⋅ 26 mV / 30 µA), d. h. der differentielle Widerstand der Diode wäre wesentlich kleiner als R38, die Dioden würden bereits klippen.
Das bedeutet, dass die Ausgangsspannungen des Filters bei tiefen Frequenzen groß genug sein können, um die nachfolgenden Dioden leitend zu machen, d. h. dass in dieser Schaltung aller Voraussicht nach mit den Dioden nur „in den Bässen die Spitzen abgeschnitten“ werden.
Das erinnert wohl nicht zufällig an die typische, leicht komprimierende und „leicht in den Bässen schmierende“ Übersteuerung / Verzerrung von „amerikanischen“ Verstärkern.
Nun zum Gesamtfrequenzgang der Zerrstufen des BOSS Blues Drivers: Der Verweis auf einen Low cut wie in einem Tubescreamer (eine −3-dB-Frequenz von etwa 700 Hz) in der Beschaltung des ersten diskreten Operationsverstärker ist dabei aber, was den gesamten Frequenzgang des Gerätes vor der Verzerrung angeht, nur die halbe Wahrheit – durch besagten Low cut und die nachfolgende Filterschaltung wird eine zu den hohen Frequenzen wesentlich sanfter ansteigende Verstärkung erreicht. (siehe dazu Abbildung 6 ) Das erspart dem Anwender zum einen die etwas penetrante Mittendominanz, dem man beispielsweise dem Tubescreamer nachsagt, und macht den Klang für nachfolgende eher dezentere Verzerrungen geeigneter (soll heißen, als Booster für modernere Metalsounds wäre der Blues Driver weniger geeignet, er könnte hier wohl zu stark „matschen“).
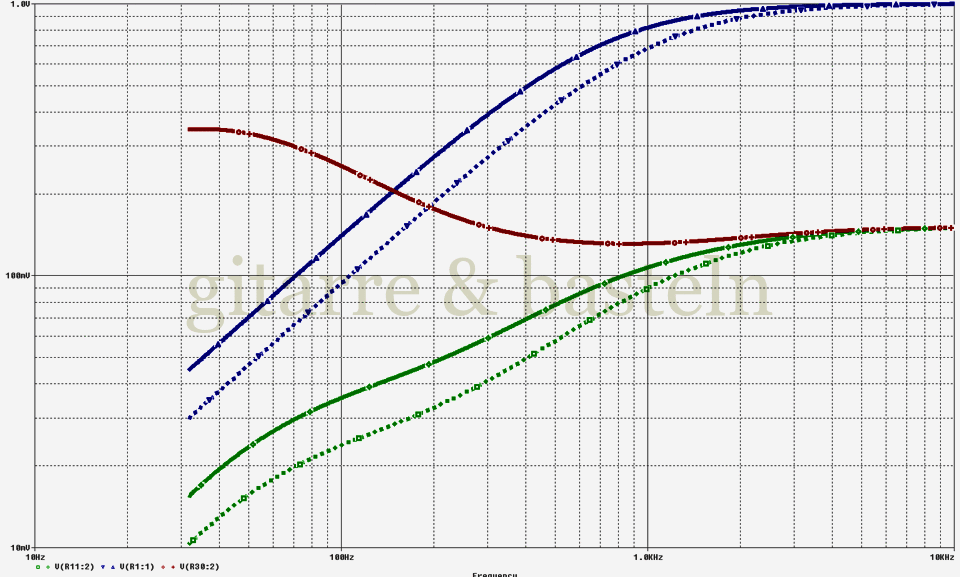

Abb. 6: Frequenzgang vor dem zweiten
diskreten Operationsverstärker
im BOSS Blues Driver (volle Linien) und
im Digitech Screamin' Blues
(gestrichelte Linien):
– Blauer Graph: Signal nach dem ersten diskreten Operationsverstärker,
– grüner Graph: Signal nach dem Fender-Tonestack und
– roter Graph: Frequenzgang des Fender-Tonestacks
Der zweite diskrete Operationsverstärker wird eher freqenzneutral gegengekoppelt (die −3-dB-Frequenz liegt bei 70 Hz), es werden – „BOSS-typisch“ – lediglich Subbässe herausgefiltert – danach folgt die Klangfilterung (siehe die folgende Abbildung 7).
Die Filterschaltung
Nach der Betrachtung der Zerrstufen und der diskreten Operationsverstärker nun also zur nachfolgenden „post-boost“-Filtereinheit, die, im Gegensatz zur bisherigen Schaltung des BOSS Blues Drivers, eher clean arbeiten soll:
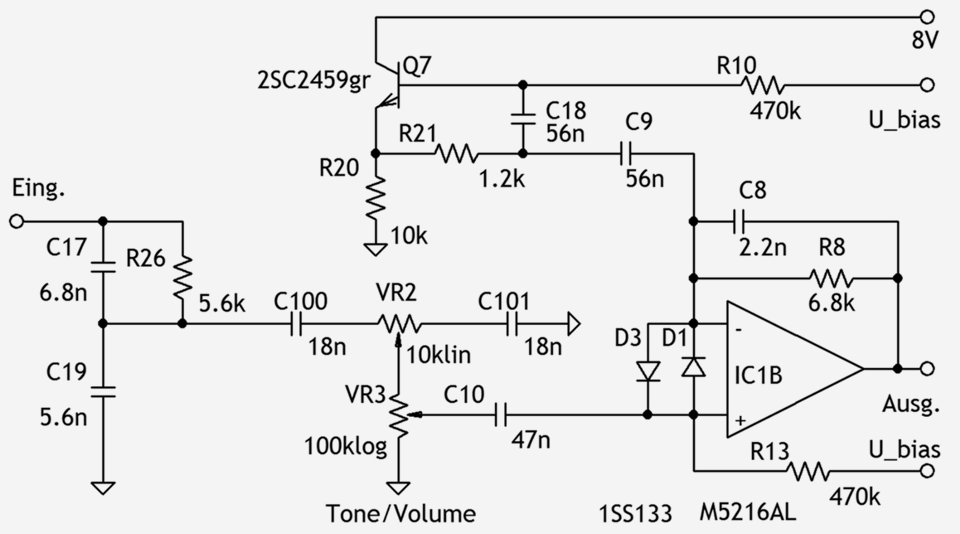

Abb. 7: Schaltung der Klangfilterstufen des BOSS Blues Driver.
Einer passiven Höhenblende folgen ein (hochohmigerer) Volumenregler und anschließend ein „richtiger“ Operationsverstärker in nichtinvertierender Schaltung. Im Fußzweig der Gegenkopplung dieses Operationsverstärkers liegt ein Serienschwingkreis aus einem Kondensator und einem mit einem Transistor realisierten Gyrator (C9, C15 und Q7 sowie R10 und R21). Der Serienschwingkreis hat eine Resonanzfrequenz von etwa 120 Hz.
Insgesamt kann man sagen, dass die durch die breite Bassabsenkung vor der Verzerrung entstandene Mittenbetonung über eine schmalbandige Bassanhebung klanglich etwas ausgeglichen wird, ohne dass die Gefahr von „Monsterbässen“ oder einem allzu intransparenten Ton mit zu viel Mulm in Bässen und tiefen Mitten besteht.
Eine Anmerkung noch zu den beiden Dioden an den Eingängen des Operationsverstärkers: Diese dienen dem Schutz dieser Eingänge vor zu großen Differenzspannungen; im Normalfall „versucht“ der Operationsverstärker ohnehin, den Ausgang so einzustellen, dass an beiden Eingängen dieselbe Spannung anliegt (das ist seine Aufgabe bzw. Funktion). Es hat also wenig Sinn, den Zerrklang des Gerätes durch Austausch dieser Dioden gegen andere Typen aufwerten zu wollen.
Die folgende Abbildung 8 zeigt den Frequenzgang der gesamten Filtereinheit bei verschiedenen Einstellungen des Tone-Reglers. Es ist zu erkennen, dass der Ausgangssignalpegel auch bei Übersteuerung des davor liegenden diskreten Operationsverstärkers praxisgerecht ist (aus einem Signal mit einem Effektivwert von 3 V am Eingang der Klangregelschaltung entsteht ein Ausgangssignal von etwa 250 mV bei Mittelstellung des Volumenreglers).
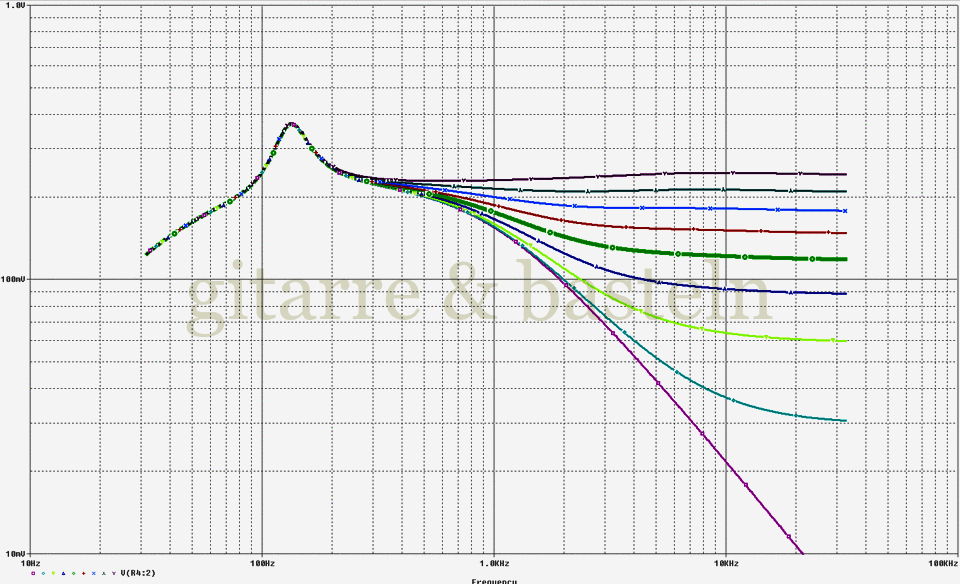

Abb. 8: Frequenzgang der Klangfilterung im BOSS Blues Driver in Abhängigkeit vom Tone-Regler. Es wurde am Eingang des Klangfilters ein Signal mit einer Amplitude von 3 V eingespeist; der Level-Regler war etwa auf Mittelstellung (Signaldämpfung auf etwa 15 %) eingestellt.
Digitech Screamin' Blues
Kapitelinhalt:[ Überspringen ]- Verringertes Gain durch andere JFETTransistoren •
- Veränderter Hochpass •
- Bassregler •
- Interner Pufferverstärker •
- Recording Out •
- Umschaltung
Nach den eingehenden Betrachtungen zur Schaltung des BOSS Blues Drivers nun zur Schaltung des Digitech Screamin' Blues. Es gibt einige Unterschiede zwischen dem BOSS Blues Driver und den Digitech Screamin' Blues (respektive CGIANT Warm Blues). Zum Vergleich der Schaltungen wird auf einen Schaltplan des Digitech Screamin' Blues, gefunden auf der Seite des „Telecaster Forums“ TDPRI, Bezug genommen. Dazu wurden auch hier – aus Gründen des Urheberrechtes – einige Teile des Schaltplans nachgezeichnet.
Verringertes Gain durch andere JFET-Transistoren
Einer der ersten (im Signalweg) auffälligen schaltungstechnischen Unterschiede zwischen dem BOSS Blues Driver und dem Digitech Screamin' Blues liegt in der Verwendung anderer (möglicherweise einfach preiswerterer) JFET-Transistoren in den diskreten Operationsverstärkern – Digitech verwendet hier nicht 2SK184, sondern J112.
Im Datenblatt des J112 (siehe Abbildung 9) wird für einen Sourcestrom von 0,3 mA bzw. 0,7 mA eine Steilheit von etwa 3,5 mS bzw. etwa 6 mS ausgewiesen. Die Gesamtsteilheit des JFET-Differenzverstärkers liegt so beim Screamin' Blues bei etwa 2,2 mS gegenüber den etwa 3,5 mS beim BOSS Blues Driver, was sich voraussichtlich in einem subtil geringeren Gain und einer ebenso subtil weicheren Kennlinien zeigen könnte. (Dabei muss berücksichtigt werden, dass das Gain, d. h. die Verstärkung der diskreten Operationsverstärker wesentlich durch die Gegenkopplung, d. h. durch die Einstellung des Gain-Reglers bestimmt wird.)
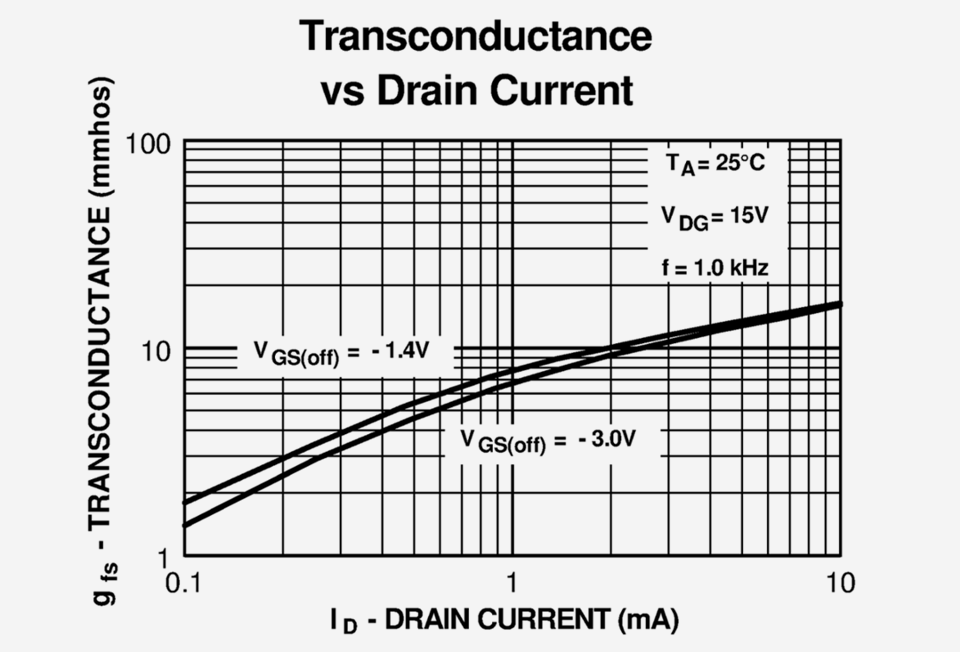

Abb. 9: Steilheit des JFET J201 in Abhängigkeit vom Sourcestrom – Auszug aus dem Datenblatt des Herstellers.
Veränderter Hochpass
Der Hochpass in der Gegenkopplung des ersten diskreten Operationsverstärkers (bei etwa 700 Hz) setzt beim Digitech bei über 1 kHz an (der untere Pfad des Gegenkopplungsspannungsteilers besteht bei BOSS aus R31 = 1,5 kΩ und C6 = 150 nF und bei Digitech aus R18 = 1 kΩ und C6 = 150 nF.), so dass der Verzerrer mit weniger Bässen, mit weniger Mitten und mehr Höhen angesteuert wird.
Bassregler
Die Bassanhebung bei 120 Hz, die beim BOSS Blues Driver fest eingestellt ist, kann beim Screamin' Blues in ihrer Höhe verändert werden – die Bässe können genauso auch schmalbandig abgesenkt werden. Wozu auch immer. Der Gyrator wird hier mit einem Operationsverstärker (U1-A) realisiert:
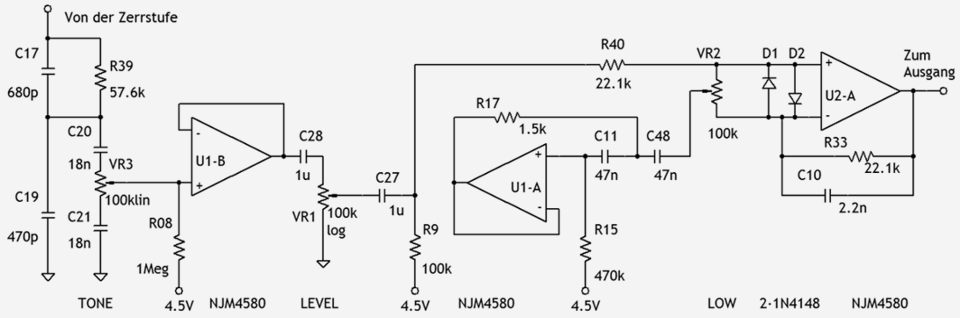

Abb. 10: Schaltung des Klangfilters im Digitech Screamin' Blues.
Auch der Bassregler des Digitech Screamin' Blues wurde simuliert – Abbildung11 zeigt das Ergebnis:
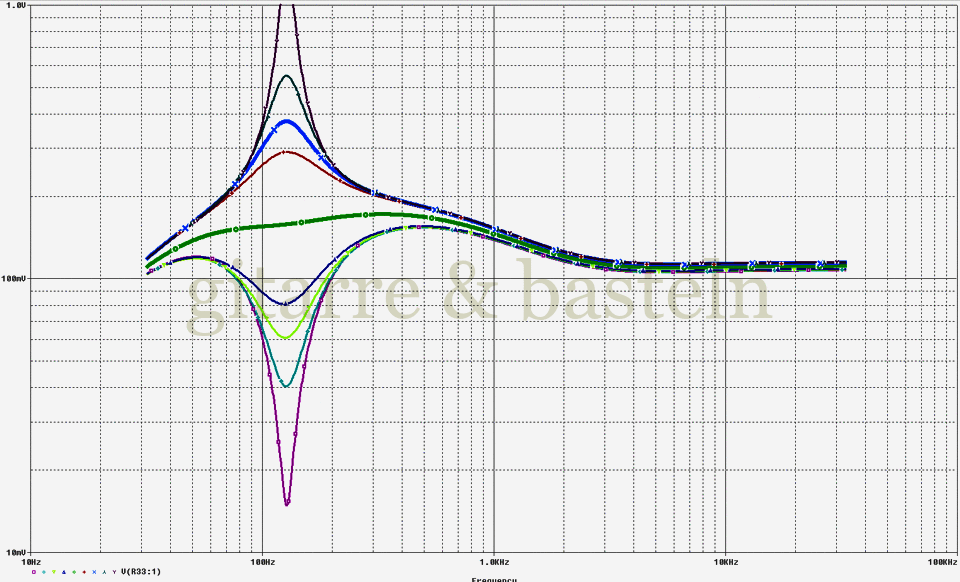

Abb. 11: Frequenzgang der Klangfilterung im Digitech Screamin' Blues in Abhängigkeit vom Low-Regler. Es wurde am Eingang des Klangfilters ein Signal mit einer Amplitude von 3 V eingespeist; der Tone-Regler war etwa auf Mittelstellung eingestellt, der Level-Regler ebenfalls (Signaldämpfung auf etwa 15 %).
Interner Pufferverstärker
Weiterhin unterscheiden sich auch die Schaltungen zur Bassanhebung – während beim Blues Driver der Eingang dieser Stufe so hochohmig ist wie der Eingang des Operationsverstärkers, findet sich beim Screamin' Blues eine übliche aktive Klangregelschaltung mit einem weitaus geringeren Eingangswiderstand, ihr wurde deshalb ein Pufferverstärker (U1-B) vorgeschaltet, damit die regelbarere Bassanhebung nicht die vorgeschaltete passive Höhenblende beeinflusst.
Der höhere Eingangswiderstand dieses Pufferverstärkers ermöglicht es wiederum, diese Höhenblende (C20, C21 und VR3) um den Faktor zehn hochohmiger zu machen. Das heißt, sie beeinflusst das Übersteuerungsverhalten des davorliegenden zweiten diskreten Operationsverstärkers nicht mehr.
Die folgende Abbildung 12 zeigt den Gesamtfrequenzgang der Klangregelschaltung beim Digitech Screamin' Blues – der Bassregler wurde in der Simulation so eingestellt, dass der Gesamtklang im Bassbereich etwa dem des BOSS Blues Drivers entspricht.


Abb. 12: Frequenzgang der Klangfilterung im Digitech Screamin' Blues in Abhängigkeit vom Tone-Regler. Es wurde am Eingang des Klangfilters ein Signal mit einer Amplitude von 3 V eingespeist; der Level-Regler war etwa auf Mittelstellung (Signaldämpfung auf etwa 15 %) eingestellt, der Low-Regler auf 0,9 (Anhebung wie beim BOSS Blues Driver).
Recording Out
Der Digitech hat (wie auch der CGIANTs Warm Blues), einen zweiten, frequenzkorrigierten Ausgang, um mit dem Gerät direkt ins Pult oder den Rechner gehen zu können (C41 …, R72 … sowie U3-A und U3-B). Dabei wird über einen Tiefpass, mit einer leichten Resonanzüberhöhung bei 2–3 kHz (laut Schaltung des Digitech), das gröbste „Verzerrerkratzen“ herausgefiltert. Diesen Filter hat Digitech auch bei anderen Verzerrern eingefügt.
Die Abbildungen Abbildung 13 und Abbildung 14 zeigen die (Simulations)schaltung und den (simulierten) Frequenzgang dieses Filters vor dem Recording Out:


Abb. 13: Schaltung des Speakersimulationsfilters im Digitech Screamin' Blues
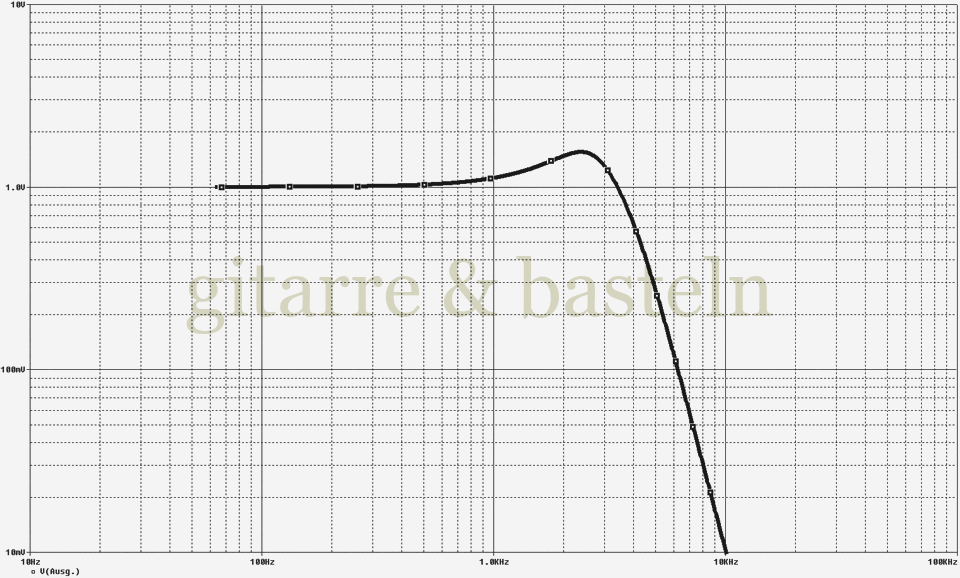

Abb. 14: Frequenzgang des Speakersimulationsfilters im Digitech Screamin' Blues
Umschaltung
Bei allen drei besprochen Geräten erfolgt die Signalumschaltung über JFET-Transistoren, die in den entsprechenden Signalpfaden liegen. Die Ansteuerung dieser JFET-Transistoren übernimmt bei BOSS ein mit diskreten Transistoren realisiertes Flipflop, bei Digitech eine Schaltung mit den MOSFET-Array CD4007. Da diese Schaltung in den Schaltplänen verschiedener Effektgeräte von Digitech regelmäßig anders dimensioniert wird und der Autor das nicht vollständig nachprüfen kann, wird hier auf eine weitere Diskussion der Schaltung verzichtet. Es ist jetzt nicht zu erkennen, welche der beiden Lösungen besser oder schlechter ist.
Abschluss und Siegerehrung
Da dem Autor von den drei hier diskutierten Geräten nur eines konkret vorliegt (CGIANT Warm Blues), der Aufbau einiger Geräte von BOSS aber aus der Vergangenheit bekannt ist, werden hier also die Geräte von BOSS mit der Kopie einer Kopie eines Originals verglichen, wobei, was die eigentliche Schaltung betrifft, das Digitech Screamin' Blues meist mit gemeint ist.
Die mechanische Konstruktion ist bei BOSS generell besser – bei BOSS werden (oder zumindest wurden) Teile, die mechanisch von außen belastet werden können, nicht direkt mit der Hauptplatine verbunden. Ob Fußtaster, Potentiometer oder die Buchsen, sie sind lediglich mit dem Gehäuse verschraubt; der Kontakt zur Platine erfolgt über Kabel (flexible Litze). Da ist CGIANTs Warm Blues wesentlich einfacher und billiger gebaut.
Dazu kommt, dass beide „Nachbauten“ im Gegensatz zu BOSS in SMD realisiert sind – für den Bastler oder besser „Tuner“ ist das natürlich eher ungünstig, weil bei SMD kaum Modifikationen der Schaltung möglich sind.
Ob die Umsetzung der Schaltung in SMD einen negativen Einfluss auf die Zuverlässigkeit eines Gerätes hat, kann hier mangels Erfahrung nicht beurteilt werden – oben wurde allerdings ausgeführt, dass der aufwendigere und teurere Aufbau bei BOSS Vorteile in der Zuverlässigkeit bieten kann.
Die Zuverlässigkeit nach Modifikationen hingegen, so zumindest die durchaus auch traurige Erfahrung des Autors, korreliert auch mit Planung und technischen Verständnis. Soll meinen, Modifikationen wie die, die unter Grenzfrequenz der Eingangsstufe von 7 Hz auf 4 Hz zu senken (Eingangskoppelkondensator von 47 nF auf 100 nF) oder die, eine der Schutzdioden vor den Eingängen des letzten Operationsverstärkers (Bassanhebung) gegen eine LED zu tauschen, sind nach Meinung des Autors nicht nur unsinnig, sondern tragen auch nicht unbedingt zu einer höheren Zuverlässigkeit des Gerätes bei.
Sollte dieser Artikel dazu beigetragen haben, die Schaltung der Geräte zu verstehen und das eine oder andere „Tuning“ besser zu planen bzw. die Schaltung hier zielgerichteter zu verändern, wäre das gut und sinnvoll genug.
