VOX Pathfinder 10 – Teil III
Endstufe – Entdämpfung des Lautsprechers
Kapitelinhalt:[ Überspringen ]Ein kleiner Übungsverstärker mit einer kleinen integrierten Endstufe und einem guten Lautsprecher bietet sich an, mit der Beschaltung der Endstufe und insbesondere mit deren Ausgangswiderstand zu experimentieren.
Ziel war es, eine Beschaltung zu finden, die den dynamischen Ausgangswiderstand des Verstärkers erhöht und dem Lautsprecher einige „Freiheiten“ lässt.
Ein bisschen Theorie
Dieser dynamische Ausgangswiderstand hat nichts damit zu tun, ob man eine Box mit 4 Ω oder 8 Ω an den Verstärker anschließt. Er beschreibt, inwieweit der Verstärker den Lautsprecher bedämpft.
Bei einen üblichen Hi-Fi-Verstärker der Ausgangswiderstand sehr gering; man versucht hier Verstärker zu bauen, die den Lautsprecher möglichst vollständig kontrollieren. Dazu wird vor allem die Spannung über dem Lautsprecher kontrolliert und dafür gesorgt, dass der Verstärker Strom liefern kann, ohne dass die Ausgangsspannung des Verstärkers einbricht.
Bei einem Gitarrenverstärker ist das nicht unbedingt erwünscht, die Resonanzen des Lautsprechers in der Box sollen durchaus auch zur Geltung kommen.
„Elektronisch“ bedeutet das, dass der Verstärker dem Lautsprecher nicht nur eine bestimmte Spannung „aufzwingt“, sondern – je nach Widerstand des Lautsprechers – in der Ausgangsspannung „nachgibt“ oder eine größere Ausgangsspannung zulässt. Im Extremfall (sehr hoher dynamischer Ausgangswiderstand, zum Beispiel beim VOX AC30) zwingt der Verstärker dem Lautsprecher keine Spannung auf, sondern „pumpt“ Strom in den Lautsprecher.
Mathematisch kann man den dynamischen Ausgangswiderstand berechnen als Quotient aus Leerlaufspannung und Kurzschlussstrom. Aber bitte nur berechnen, nicht ausprobieren! Man berechnet also, welche Ausgangsspannung der Verstärker ohne Last hätte und welcher Strom theoretisch fließen würde, wäre der Ausgang kurzgeschlossen.
Für die Erhöhung des Ausgangswiderstands gibt es schaltungstechnisch mehrere Möglichkeiten. Ihnen ist gemeinsam, dass nicht nur die Ausgangsspannung des Verstärkers, sondern auch dessen Ausgangsstrom (abhängig vom Lautsprecher) in die Gegenkopplung einfließt.
Schaltung und Berechnung
Dafür gibt es schaltungstechnisch verschiedene Möglichkeiten, eine Serien- oder eine Parallelschaltung von Spannungs- und Stromgegenkopplung sowie Mischformen. Diese alle zu erläutern würde wohl den Rahmen dieses Textes sprengen – es wird im Folgenden die realisierte Schaltung vorgestellt.
Zunächst aber erst einmal die Originalschaltung der Endstufe des Verstärkers.
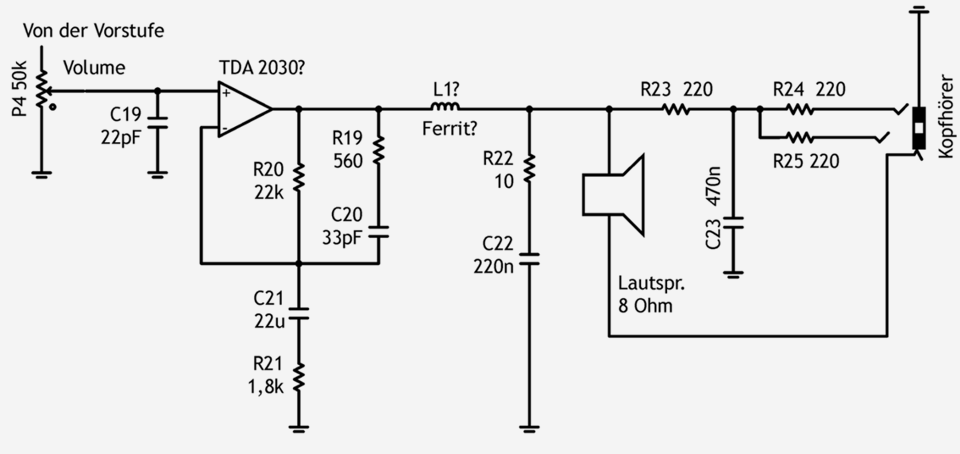

Abb. 3.1: Endstufe des Verstärkers VOX Pathfinder 10. (Angaben ohne Gewähr.)
Die Beschaltung des TDA2030 unterscheidet sich kaum von der im Datenblatt angegebenen, lediglich ist der Verstärkungsfaktor der Gesamtschaltung durch einen größere Gegenkopplung kleiner, so das sich für eine Eingangsspannung von 775 mV (0 dB) in etwa Vollaussteuerung ergibt. Dies wurde durch den veränderten Wert von R21 erreicht. Es wird über den Spannungsteiler R20 (22 kΩ) und R19 (1,8 kΩ) etwa ein dreizehntel der Ausgangsspannung auf den Minus-Eingang des Verstärkerschaltkreises zurückgeführt.
C20 und R19 verringern die Verstärkung bei hohen Frequenzen und dienen der Unterdrückung möglicher Schwingungen. Die gleiche Aufgabe hat das Boucherot-Glied R22 und C22 – es gleicht die ansteigende Impedanz des Lautsprechers bei hohen Frequenzen aus.
C23 und die Widerstände R23 bis R25 bilden, so ein Kopfhörer angeschlossen ist, einen Tiefpass mit einer Grenzfrequenz von etwa 4 kHz. Weiterhin schaltet die Kopfhörerbuchse die Masseverbindung des Lautsprechers ab, wenn ein Kopfhöhrerstecker eingesteckt ist, der Lautsprecher hängt dann „in der Luft“, ist also stumm.
Nun zur modifizierten Endstufenschaltung mit gemischter Spannungs- und Stromgegenkopplung. Was wurde hier gemacht?
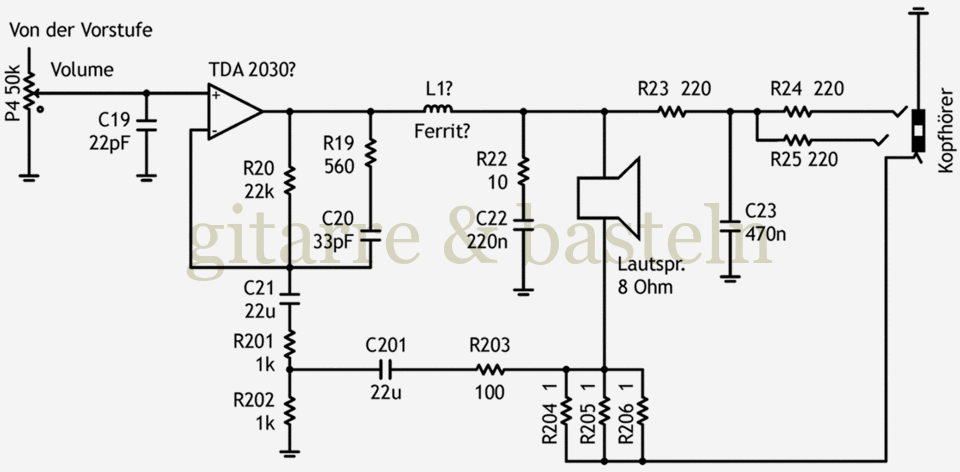

Abb. 3.2: Schaltung einer gemischten Spannungs-/ Stromgegenkopplung in der Endstufe.
Der Widerstand R21 (1,2 kΩ) wurde durch zwei Widerstände R201 und R202 mit je 1 kΩ ersetzt. Das ist weniger einem besonderen Schaltungsdesign geschuldet, sondern eher einer einfachen „löttechnischen“ Umsetzung – sie ermöglicht es, in die Lötpunkte des vorherigen Widerstandes R21 die beiden Widerstände R201 und R202 einzusetzen, an deren Verbindung die Stromgegenkopplung eingespeist wird, wie im folgenden Foto zu sehen:


Abb. 3.3: Einspeisung der Stromgegenkopplung in die vorhandene Schaltung (unten Mitte links; rechts neben dem kleinen Schalter
Zur (elektronischen) Funktion: Zwischen den beiden Widerständen R201 und R202 wird über einen Koppelkondensator C201 und einen weiteren Widerstand R203 ein Signal zur Stromgegenkopplung eingespeist, das durch Einschleifen von drei parallelen Widerständen R204 bis R206 mit je 1 Ω in die Lautsprecherleitung gewonnen wurde.
Um zu verstehen, wie die beiden Gegenkopplungsarten wirken, werden diese im Folgenden einzeln beschrieben. Dabei werden alle außerhalb des (Gitarren)tonfrequenzbereiches wirkenden Bauelemente ausgeklammert – insbesondere R19 (wirkt mit C20 im Ultraschallbereich gegen Schwingneigung der Endstufe) sowie C21 und C201 (Gleichspannungstrennung und Dämpfung im Subbassbereich).
Zur Funktion der Spannungsgegenkopplung muss der Leerlauf betrachtet werden. In diesem Fall wird die Ausgangsspannung über R20 (22 kΩ), R201 (1 kΩ) und R202 || R203 (zusammen etwa 90 Ω) geteilt. (R204 bis R206 können hier vernachlässigt werden.)
Begonnen wird mit dem Spannungsteiler, mit dem die Ausgangspannung im Leerlauf auf den invertierenden Eingang zurückgeführt wird:
\( \begin{equation} u_{\textrm{E}} = \cfrac{R_{\textrm{203}}||R_{\textrm{202}} + R_{\textrm{201}}} {R_{\textrm{203}}||R_{\textrm{202}} + R_{\textrm{201}} + R_{\textrm{20}}} \cdot u_{\textrm{LL}} \tag{1}\end{equation} \)
Diese Gleichung wird nach uLL / uE umgestellt
\( \begin{equation} \cfrac{u_{\textrm{LL}}}{u_{\textrm{E}}} = \cfrac{R_{\textrm{203}}||R_{\textrm{202}} + R_{\textrm{201}} + R_{\textrm{20}}} {R_{\textrm{203}}||R_{\textrm{202}} + R_{\textrm{201}}} \tag{2}\end{equation} \)
ein wenig vereinfacht
\( \begin{equation} \cfrac{u_{\textrm{LL}}}{u_{\textrm{E}}} = \cfrac{R_{\textrm{20}}} {R_{\textrm{203}}||R_{\textrm{202}} + R_{\textrm{201}}} \tag{3}\end{equation} \)
und es werden die konkreten Widerstandswerte eingesetzt:
\( \begin{eqnarray} \frac{u_{\textrm{LL}}}{u_{\textrm{E}}} & = & 1 + \frac{22\,\textrm{k}Ω} { 1\,\textrm{k}Ω \,||\,100\,Ω + 1\,\textrm{k}Ω} \\~\\ & = & 1 + \frac{22} {0{,}091 + 1} \\~\\ u_{\textrm{LL}} & \approx{} & 21{,}167 \cdot u_{\textrm{E}} \tag{4}\end{eqnarray} \)
Rechnerisch hat die Endstufe also eine Leerlaufausgangsspannung von (etwa) dem 22-fachen der Eingangsspannung.
Die Funktion der Stromgegenkopplung hingegen zeigt sich am besten im (gedachten!) Kurzschlussfall. In diesem Fall ist die Spannung über den parallelgeschalteten Widerständen R204 bis R206 gleich der am Ausgang der Endstufe. Aus dem Kurzschlußstrom, multipliziert mit 1 Ω / 3, ergibt sich also die Ausgangsspannung der Endstufe, aus der sich nach zwei Spannungsteilerstufen die Spannung am invertierenden Eingang der Endstufe und deren Eingangsspannung ableiten läßt. Bei dieser Berechnung wurde allerdings vernachlässigt, daß die Spannungsteiler sich gegenseitig belasten (R202 und R203 belasten R204 ff, R20 und R201 belasten R203). Da aber R202 und R203 wesentlich größer sind als R204 ff und weiterhin R201 und R20 wesentlich größer sind als R203, kann diese Belastung hier ignoriert werden.
Zunächst also die Grundgleichung für die Stromgegenkopplung (Schaltung im Kurzschlussfall). Die Eingangsspanung des invertierenden Eingangs uA setzt sich aus zwei Spannungen zusammen – der Spannung über R202 und der Spannung über R203, wobei letztere der über dem Spannungsteiler R20 und R201 geteilten Spannung über R203 entspricht.
\( \begin{eqnarray} u_{\textrm{E}} & = & \frac{R_{\textrm{202}}} {R_{\textrm{202}} + R_{\textrm{203}}} \cdot{} u_{\textrm{A}} \\~\\ & + & \frac{R_{\textrm{201}}} {R_{\textrm{201}} + R_{\textrm{20}}} \cdot \frac{R_{\textrm{203}}} {R_{\textrm{202}} + R_{\textrm{203}}} \cdot{} u_{\textrm{A}} \tag{5}\end{eqnarray} \)
Die Ausgangsspannung UA wiederum ist im Kurzschlussfall gleich der Spannung über den parallelgeschalteten Widerständen R204 ff.
\( \begin{equation} u_{\textrm{A}} = \cfrac{R_{\textrm{204}}}{3}\cdot i_{\textrm{KS}} \tag{6}\end{equation} \)
Im folgenden werden beide Gleichungen zusammengefasst, der Kurzschlussstrom iKS wird extrahiert und es werden konkrete Werte eingesetzt:
\( \begin{equation} u_{\textrm{E}} = \cfrac{1\,Ω}{3} \left( \cfrac{1\,\textrm{k}Ω} {1{,}1\,\textrm{k}Ω} + \cfrac{1\,\textrm{k}Ω} {23\,\textrm{k}Ω} \cdot \cfrac{100\,Ω} {1{,}1\,\textrm{k}Ω} \right) \cdot i_{\textrm{KS}} \tag{7}\end{equation} \)
Für eine einfachere numerische Lösung werden rechts die Widerstände innerhalb der Klammern durch 0,1 kΩ geteilt:
\( \begin{eqnarray} u_{\textrm{E}} & = & \frac{1 Ω}{3} \cdot \left(\frac{10}{11} + \frac{1}{23} \cdot \frac{1}{11} \right) \cdot i_{\textrm{KS}} \\~\\ & = & 1 Ω \cdot \frac{231} {3\cdot 11 \cdot 23} \cdot i_{\textrm{KS}} \tag{8}\end{eqnarray} \)
Schließlich wird nach iKS aufgelöst:
\( \begin{equation} i_{\textrm{KS}} \approx \cfrac{3{,}3}{Ω} \cdot u_{\textrm{E}} \tag{9}\end{equation} \)
Der Ausgangskurzschlusstrom ergibt sich also zur Eingangsspannung, dividiert durch 3,3 Ω. Für diese Schaltung berechnet sich jetzt der dynamische Ausgangswiderstand mit etwa 6 Ω:
\( \begin{eqnarray} r_{\textrm{out}} & = & \frac{u_{\textrm{LL}}}{i_{\textrm{KS}}} \\~\\ & = & \frac{21{,}167} {3{,}3} \cdot \Omega \cdot \frac{u_{\textrm{E}}} {u_{\textrm{E}}} \\~\\ r_{\textrm{out}} & \approx{} & 6{,}4 \Omega{} \tag{10}\end{eqnarray} \)
Der differentielle Ausgangswiderstand liegt also etwa in Größenordnung der Lautsprecherimpedanz. Für den Frequenzgang der Endstufe bedeutet das, dass die Spannungsverstärkung bei Frequenzen, bei denen die Impedanz des Lautsprechers stark ansteigt, maximal auf den doppelten Wert steigen kann. Das soll in einer Simulation untersucht werden.
Simulation
Diese Schaltung wurde in PSPICE simuliert. Zur Simulation des komplexen Widerstands des Lautsprechers kam ein Modell zum Einsatz, das einem Patent der Firma GrooveTubes von 1990 entnommen wurde (US Patent Nr.: 4,937,874; gefunden in der Patent-Liste von AMZ – siehe Patent 43). Hier die verwendete Simulationsschaltung, die Lautsprechersimulation ist blau gezeichnet.
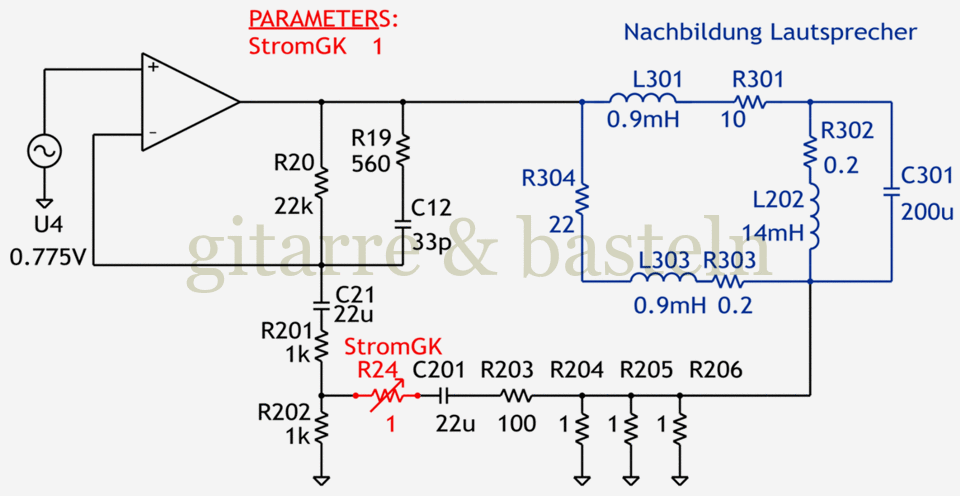

Abb. 3.4: Schaltung zur Simulation der gemischten Spannungs-/ Stromgegenkopplung in der Endstufe. Die Simulationsschaltung des Lautsprechers ist blau. Der rote Widerstand R24 schaltet die Stromgegenkopplung zu (R24 = 1 Ω) oder ab (R24 = 1 MΩ).
In der folgenden Abbildung 3.5, die den simulierten Frequenzgang der Endstufe mit und ohne Stromgegenkopplung darstellt, sind die Anhebungen um die Bassresonanz und in den Höhen durch die Stromgegenkopplung deutlich zu erkennen. Sie scheinen nicht besonders hoch zu sei zu sein, wobei das zum Teil in der speziellen Ersatzschaltung für den Lautsprecher begründet ist. Im Bassbereich liegt deren maximale Impedanz (R304) dieser Schaltung beim etwa dreifachen der Gleichstromimpedanz (R301||R304). Insgesamt ist aber die Anhebung der Ausgangsspannung im Bassbereich auf das etwa eineinhalbfache nachvollziehbar, wenn man den differentiellen Ausgangswiderstand von etwa 6 Ω und die geringe besprochene Ausprägung der Bassresonanz gleichzeitig einberechnet.
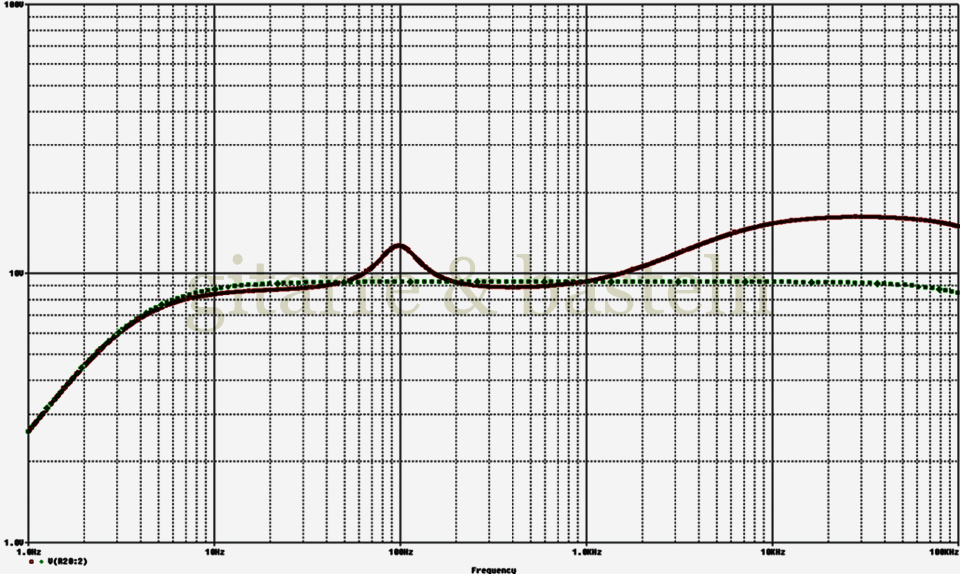

Abb. 3.5: Simulierter Frequenzgang der gemischten Spannungs-/ Stromgegenkopplung in der Endstufe. Der gestrichelte Graph zeigt den den simulierten Frequenzgang der Endstufe ohne Stromgegenkopplung.
