Hier geht es nicht um Elektronik, sondern um (technische und gestalterische) Lösungen bei der Erstellung dieser Seite: Zunächst Teaser-Bilder bzw. Vignetten. Dazu die technische Bildbearbeitung – mit Oszillogrammen und Abbildungen. Dazu ein Script zur Berechnung von Obertonspektren. Am Schluss der „Darkmode“ in Text und Bild.
Kolophon
Kapitelinhalt:[ Überspringen ]- Vignetten zu Artikeln / Artikelteaser •
- (Technische) Bildbearbeitung •
- Script zur Berechnung von Obertonspektren •
- Ein Darkmode-Layout für die Seite
Vignetten zu Artikeln / Artikelteaser
Kapitelinhalt:[ Überspringen ]- Vignette zur Auflistung der Verolayouts •
- Vignette zum Artikel über Treble Booster •
- Vignette zum Artikel über das Colorsound Tremolo
Vignette zur Auflistung der Verolayouts
Ein passend konstruiertes Icon für eine Auflistung von VERO-Layouts: Hintergrund war zunächst ein Wortspiel / eine Wortähnlichkeit zwischen den Wörtern VERO(-Layouts) und SERO (VEB Kombinat Sekundärrohstoffe – DDR-Recyclingfirma) sowie die Erinnerung an das hemdsärmelige, aber durchaus „mathematisch-technisch“ gestaltete Logo dieser Recyclingfirma.
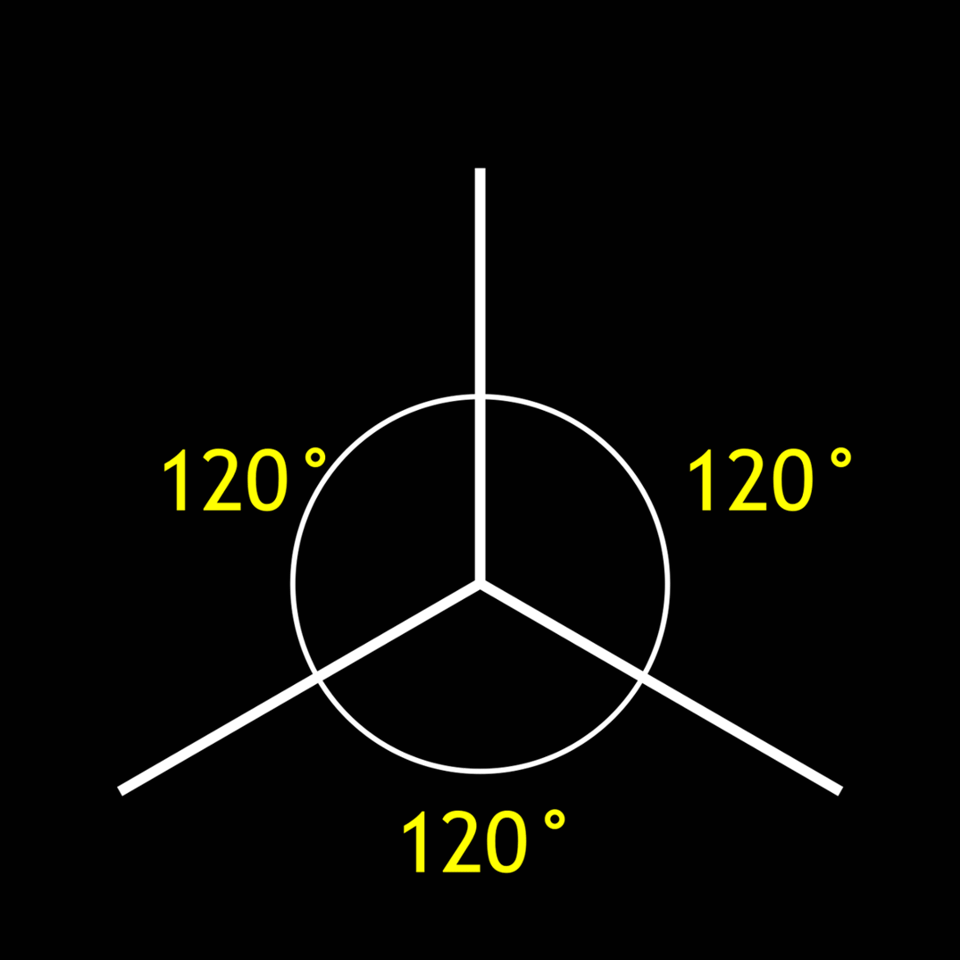
Begonnen wird mit der bildlichen Erklärung in Abbildung 1.1. Links das alte SERO-Logo (die verwendete Bilddatei für das Logo wurde unter anderem auf der Seite https://de-academic.com gefunden). Das Logo ist etwas holprig in der Isometrie gezeichnet und, zumindest in dieser Darstellung, vertikal etwas zu schmal skaliert. Im mittleren und rechten Teil der Abbildung wird versucht, das Prinzip der isometrischen Darstellung deutlich zu machen:
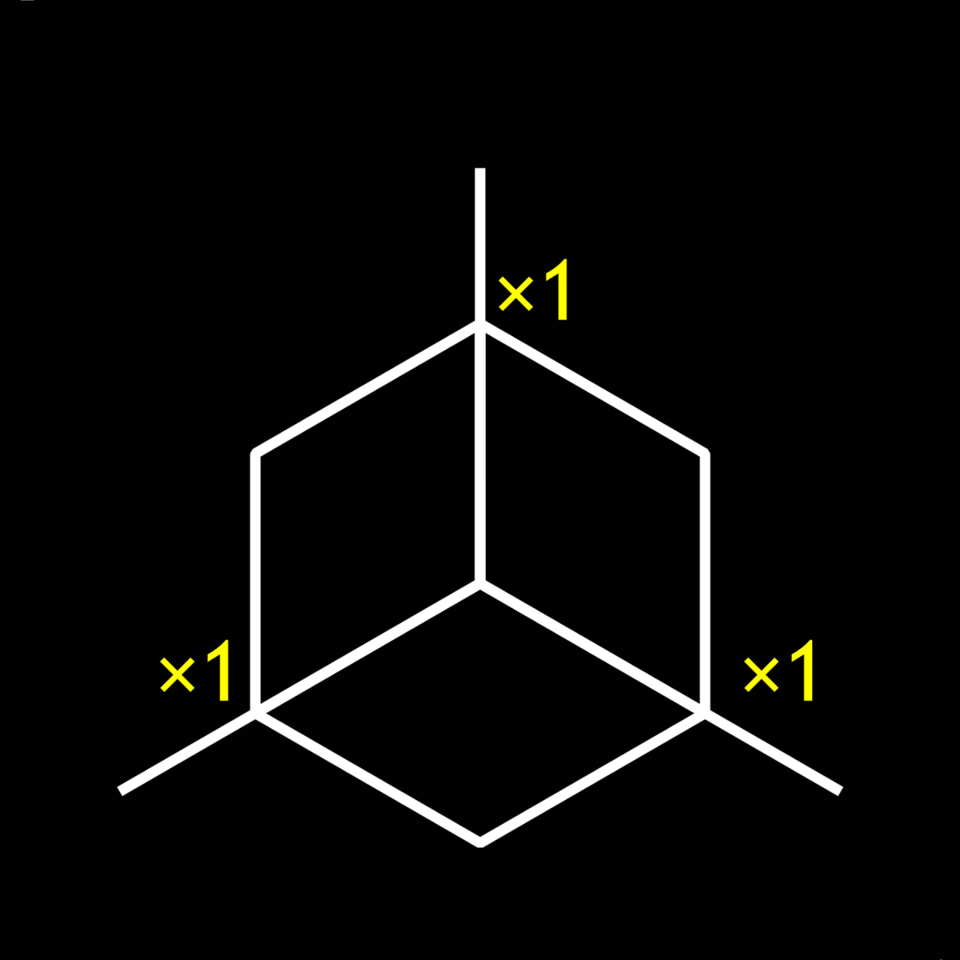
Bildertabelle 1.1: Links: SERO-Logo. Mitte und Rechts: Prinzip der räumlichen Darstellung in der Isometrie; Alle Achsen stehen in einem Winkel von 120°, in Richtungen aller Achsen wird mit Faktor eins skaliert.
Die räumlichen Achsen x, y und z werden auf drei Geraden projiziert, die zueinander im Winkel von 120° stehen. Die Koordinaten jedes Punktes werden mit gleicher Skalierung auf die drei Geraden abgetragen.
Zeichnet man so einen Würfel, so werden seine Seitenwände in der Projektion durch Rhomben (bzw. Rauten mit gleichen Seitenlängen) mit Innenwinkeln von 60° und 120° dargestellt. Jedes dieser Rhomben ließe sich zusammensetzen aus zwei gleichseitigen Dreiecken (Innenwinkel drei mal 60°) oder aus vier rechtwinkligen Dreiecken („Zeichendreiecke“ – Innenwinkel 30°, 60° und 90°) zusammensetzen. Daraus ergibt sich, dass die beiden Diagonalen des Rhombus senkrecht zueinander stehen (sonst wäre es kein Rhombus) und dass das Seitenverhältnis der beiden Diagonalen des Rhombus gleich dem Tangens von 30° ist.
Daraus leitet sich das Vorgehen bei der Konstruktion des Icons ab – begonnen wird mit der linken Seitenwand.
-
Die quadratische Seitenwand links wird – als quadratische Streifenleiterplatine – in der Draufsicht gezeichnet. Dabei werden an den Bohrungen außerhalb der Buchstaben Cuts gesetzt bzw. das Kupfer entfernt, so dass die Buchstaben „V“ und „E“ als Kupfer stehenbleiben.
-
Dieses Quadrat, d. h. die Symboldarstellung der Streifenleiterplatine, wird um 45° gedreht – dadurch sind die Diagonalen exakt senkrecht bzw. waagerecht.
-
Das gedrehte Quadrat wird jetzt vertikal so skaliert, dass aus dem gedrehten Quadrat ein Rhombus mit den Innenwinkeln 60° und 120° wird (und die Außenkanten zur Waagerechten einen Winkel von 30° und zur Senkrechten einen Winkel von 60° aufweisen ) – also mit vertikalem Skalierungsfaktor tan(30°) / tan(45°) = tan(30°) = 1 / √3 = 0,577.
-
Jetzt kann um −60° zurückgedreht werden, so dass die früheren Seitenkanten und damit die Seitenwand auch wieder senkrecht stehen.
Die folgende Abbildung 1.2 zeigt das Prinzip noch einmal in vier kleinen Bildern:
Bildertabelle 1.2: Prinzip des „Einschwenkens“ der linken Seitenwand – um 45° drehen, um tan(30°) / tan(45°) vertikal skalieren und um −60° zurückdrehen.
Das Vorgehen bei der rechten Seitenwand unterscheidet sich nur im Vorzeichen der Drehungen – vor dem Skalieren wird mit −45° gedreht und nach dem Skalieren mit +60° zurückgedreht:
Bildertabelle 1.3: Prinzip des „Einschwenkens“ der rechten Seitenwand – um −45° drehen, vertikal um tan(30°) / tan(45°) skalieren und um 60° zurückdrehen.
Bei der Deckenplatte kann die zweite Drehung entfallen – in der folgenden Abbildung 1.4 wird an dieser Stelle der Zusammenbau des VERO-Würfels angedeutet:
Bildertabelle 1.4: Prinzip des „Einschwenkens“ der Deckenplatte – um 45° drehen, vertikal mit Faktor tan(30°) / tan(45°) skalieren und über die beiden Seitenwände einmontieren.
Anschließend wird das fertig gezeichnete Bild in eine Pixeldatei exportiert,
auf die Bildbreite der Vignetten
(192 Pixel) heruntergerechnet und als
*.gif-Bild gespeichert.
Vignette zum Artikel über das Colorsound Tremolo
Icon zum Artikel über das Colorsound Tremolo – eine Montage von waagerechten und senkrechten Sinuskurven ergibt ein dreidimensionales Wellenbild: Eine hübsche Spielerei zur Illustration der akustischen Wahrnehmung eines guten „wabernden“ (nicht „stotternden“) Tremolos entstand aus der zufällig gefundenen Idee – deren Umsetzung im Folgenden in Bild und Text beschrieben wird:
Zunächst – in der ersten Bilderreihe – die Grundidee :
Bildertabelle 2.1: Pulsierender 3D-Effekt durch überlagerte Sinuskurven.
Zur obigen ersten Bilderreihe Abbildung 2.1 (obwohl eigentlich selbsterklärend):
-
Eine Kurve, in etwa eine Sinuswelle (linkes Bild),
-
wird – immer wieder mit einem leichten horizontalen Versatz – in gleichem vertikalem Abstand nach oben und unten wiederholt (mittleres Bild).
-
Diese Anordnung wird kopiert, anschließend um 90° gedreht und über die ursprüngliche Anordnung gelegt (rechtes Bild).
Es folgen die Glitzerpunkte und der rote Nagel:
Bildertabelle 2.2: Setzen der verschiedenen „Glitzerpunkte“ und des „roten Nagels“.
Also zu obiger Abbildung 2.2:
-
Die ersten vier Wiederholungen (je eine in jeder Richtung – nach oben, nach unten, nach rechts und nach links) werden „ver-und-et“ und weiß gesetzt; d. h. die Flächen, an denen sich jeweils zwei Kurven überlagern, werden aufgehellt (weiß, siehe linkes Bild).
-
Selbiges passiert mit den zweiten und dritten Wiederholungen (Aufhellung auch weiß) und auch mit den vierten, fünften etc. (Umfärbung hellblau, siehe mittleres Bild).
-
Insgesamt entsteht durch die weißen Aufhellungen eine Art „schwimmendes sich drehendes Kreuz“ mit einem roten Fixpunkt in der Mitte (gemeinsame Fläche der mittleren Kurven) und eine Art eingefärbter Ring in hellblau. (rechtes Bild).
Nun zum Hintergrund – siehe nachfolgende Abbildung 2.3
Bildertabelle 2.3: Einsetzen des Hintergrundes für mehr Tiefe und Dynamik.
-
Den Hintergrund bildet ein dunkler konzentrischer Farbverlauf von etwas heller (in der Mitte) der nach dunkler außen wird (siehe linkes Bild).
-
Es entsteht eine Art optischer Drehimpuls nach links, wenn die beiden mittleren Sinuskurven davorgehängt werden (mittleres Bild).
-
Im rechten Bild dann die fertige Grafik.
Vignette zum Artikel über Treble Booster
Ein Icon zum Artikel über Modifikationen des klassischen Trebleboosters mit Germaniumtransistoren – im konkreten Fall mit sowjetischen МП21. Die hohe Zeit dieser Technologie fiel in etwa in die Zeit des ersten Sputniks – die Illustration sollte beides in Zusammenhang bringen.
Ziel war es, einen im Artikel verwendeten Germaniumtransistor МП21 wie eine Art Sputnik vor einem Sternenhimmel schweben zu lassen. Zuerst der Sternenhimmel:
Es kann mit handelsüblichen Buntstiften, einem Scanner und einer einfachen Bildbearbeitungssoftware gearbeitet werden:
-
Die gewünschten Farben im Sternenhimmel sind schwarz und dunkelblau sowie weiß, gelb und „rötlich“ – die passenden Komplementärfarben weiß und hellgelb sowie schwarz, blau und „blaugrünlich“. Es wurde also mit Bunt- und Filzstiften auf ein weißes Blatt Papier gezeichnet (linkes Bild).
-
Das Blatt Papier wurde eingescannt und farbinvertiert (aus dem weißen wurde ein schwarzer Hintergrund, aber auch aus hellgelb dunkelblau, aus blaugrün wurde gelb etc.; siehe mittleres Bild)
-
und anschließend gedreht, beschnitten und im Farbverlauf angepasst (rechtes Bild).
Bildertabelle 3.1: Eingescannte Papierzeichnung, deren Farbinvertierung und Farbanpassung für einen Weltraumhintergrund.
Nun zum freischwebenden Transistor:
-
Ein Foto des Transistors wurde der Seite eines aktuellen Anbieters als GIF-Datei (d. h. bereits freigestellt) entnommen (linkes Bild),
-
Die äußeren Beinchen wurden im Bildbearbeitungsprogramm als eigene Objekte abgeknipst, gedreht und irgendwie wieder angesetzt (siehe mittleres Bild).
-
Der Transistor kam vor den Sternenhimmel (rechtes Bild).
Bildertabelle 3.2: Einem freigestellten Transistor werden zwei Beine abgetrennt, nach außen gebogen und wieder angesetzt, bevor das Ganze vor der Weltraumtapete schwebt.
Wird gegebenenfalls fortgesetzt. …