Ideen zu einem Treblebooster für Humbucker – Teil III
Treblebooster mit Emitterdiode
Kapitelinhalt:[ Überspringen ]- Vorüberlegungen •
- Kennlinie und Verhalten •
- Schaltungstechnische Umsetzung •
- Nachrechnen mit EXCEL •
- Zwei Schaltungsvorschläge
Im ersten Teil dieses Ideen-Artikels über Treblebooster wurde darüber nachgedacht, warum es einen hochohmigeren Treblebooster geben sollte und eine, zugegeben eher formelmathematisch-theoretische Möglichkeit skizziert. Im folgenden soll es um einen schaltungstechnisch einfacheren Ansatz gehen – in den Emitterkreis wird eine Diodenschaltung eingefügt, die Widerstände vor der Basis des Transistors werden erhöht und der Eingangskondensator verringert.
Vorüberlegungen
Die im vorherigen Abschnitt (zum „Ostfriesen“-Booster) dargestellte grundlegende Idee, den Eingangswiderstand eines Trebleboosters für die Verwendung mit Humbuckern zu zu verdoppeln, indem nur ein Treblebooster nur für einen – „oberen“ – Singlecoil des Humbuckers „arbeitet“, lässt sich anders weiterführen – zwei Treblebooster (je ein Treblebooster für eine Humbucker-Spule) könnten auch miteinander in Reihe geschaltet verschaltet werden, so, wie auch die beiden Einzelspulen des Humbuckers in Reihe geschaltet verschaltet werden, allerdings „Masse an Masse“. Die folgende Abbildung 3.1 zeigt den ersten Ansatz.

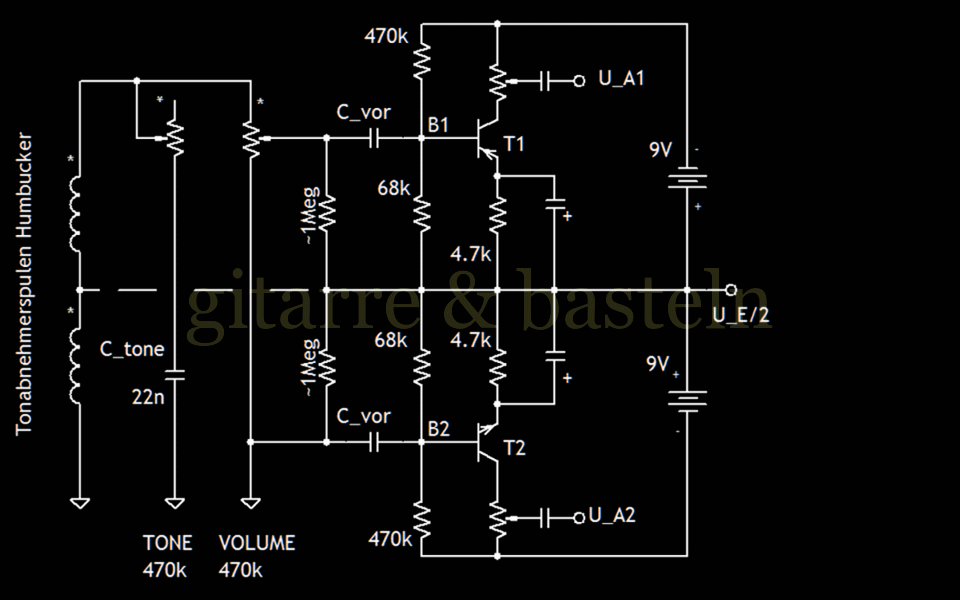
Abb. 3.1: Weiterer Ansatz für die Realisierung eines hochohmigeren Trebleboosters – das Eingangssignal wird auf zwei mit den Massen zueinanderliegende Treblebooster „aufgeteilt“.
Bezugspotential bzw. Schaltungs- und Batteriemasse in dieser eher virtuellen Schaltung wäre (bei vollaufgedrehtem Volumenregler der Gitarre) die Mitte des Humbuckers, d. h. die Verbindung zwischen beiden Einzelspulen. Am Ausgang des oberen Trebleboosters liegt dann ein Signalgemisch, bestehend aus dem Ausgangssignal dieses oberen Trebleboosters UA und dem halben Gitarrenausgangssignal UE / 2 an.
Das ist natürlich nur ein theoretischer Ansatz, da ja das halbe Tonabnehmersignal im Allgemeinen nicht außerhalb des Tonabnehmers zur Verfügung steht. Allerdings wird in Abbildung 3.2 der Faden weitergesponnen und die theoretische Schaltung ein wenig umgebaut – es wird mit den Eingangs- und den Basis-Emitter-Kreisen begonnen:

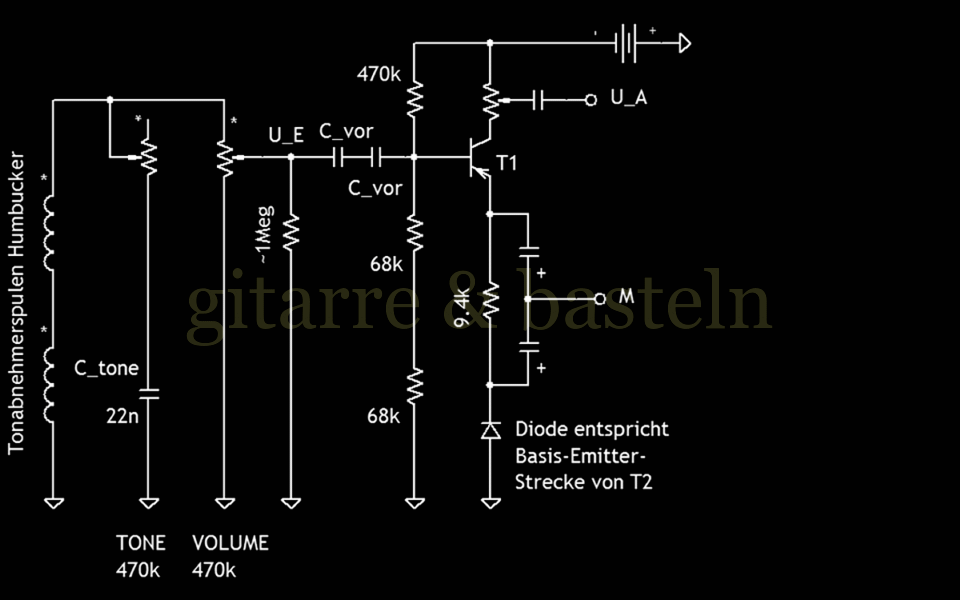
Abb. 3.2: Schaltungstechnische Vereinfachung und Umsetzung des in Abbildung 3.1 dargestellten Prinzips – der Transistor des zweiten, unteren Trebleboosters wird auf seine Basis-Emitter-Strecke reduziert.
Für diesen Schritt wurde, etwas vereinfachend, davon ausgegangen, dass alle Bestandteile dieser beiden Eingangskreise – die beiden Spulen des Tonabnehmers, der Eingangskoppelkondensator des oberen Trebleboosters, die Basis-Emitter-Strecke von dessen Transistor T1, die Emitterwiderstände beider der Transistoren beider Treblebooster, die Basis-Emitter-Strecke des Transistors des unteren Trebleboosters T2 sowie dessen Eingangskoppelkondensator signaltechnisch einen Serienstromkreis bilden, dessen Elemente in beliebiger Reihenfolgen hintereinandergeschaltet werden können und deren Massebezug verschoben werden kann. Zuerst wandert der Eingangskondensator des unteren Trebleboosters vor den Eingangskondensator des oberen.
Dabei halbiert sich zuerst der Eingangskoppelkondensator von T1; Weiterhin werden die Emitterwiderstände von T1 und T2 nebst parallelgeschalteter Kondensatoren in Serie geschaltet; d. h. der gemeinsame Emitterwiderstand wird verdoppelt und der parallelgeschaltete Kondensator halbiert.
Wenn man jetzt (als nächste Vereinfachung bzw. nächsten Kompromiss) die Sättigung von T2 bzw. deren Rückwirkung auf die Basis-Emitter-Strecke ignoriert, kann man, signalmäßig betrachtet, die Basis-Kollektor-Diode von T2 „wegschneiden“ und dessen Basis-Emitter-Strecke durch eine Diode ersetzen, welche dann statische Kennlinie wie Kleinsignalverhalten der Basis-Emitter-Strecke von T2 nachbilden muss.
Das untere Ende des Humbuckers, d. h. der Serienschaltung der beiden Tonabnehmerspulen wie auch die „ehemalige“ Basis von T2, d. h. die Anode der genannten Ersatzdiode für dessen Basis-Emitter-Strecke, werden jetzt an Masse gelegt. Damit verdoppelt sich außerdem der Widerstand zwischen der Basis von T1 und Masse, dessen Basisstromeinspeisung wird doppelt so hochohmig und die Basisvorspannung steigt.
Der ehemalige Punkt „M“, d. h. der Spannungsmittelpunkt des neue Emitterwiderstands, der auch der Spannung zwischen den beiden Einzelspulen des Humbucker entsprechen soll, hat jetzt keine Bedeutung mehr.
Gleichspannungsmäß gibt es aber eine kleine „Ungereimtheit“ – bei der Nachbildung der Basis-Emitter-Strecke eines Germaniumtransistors durch eine Diode wird eine um einen Offset größere Spannung über der Diode notwendig sein.
Zur Erläuterung: Bei Germaniumtransistoren führt deren hoher Reststrom dazu, dass auch dann Emitterströme fließen, wenn die Basis-Emitter-Spannung kleiner null (d. h. bei dem untersuchten pnp-Transistor positiv) ist (Siehe dazu auch das Diagramm in Abbildung 3.4). Wird die Basis-Emitter-Strecke nun durch eine „parameterstabilere“ Silizium- oder Schottkydiode ersetzt, so wird hier vermutlich eine größere Spannung über der Diode notwendig sein. Sollte diese Spannungsdifferenz konstant sein, hätte sie zur Nachbildung des dynamischen Verhaltens kaum Bedeutung.
Diese Zusammenhänge, d. h. das Verhalten der Basis-Emitter-Strecke eines Germaniumtransistors, wurden in einer Messschaltung genauer untersucht – dazu wurde ein Transistor AC128 mit einem ausgewiesenen Stromverstärkungsfaktor von etwa 100 in Basisschaltung „vom Emitter aus“ vermessen (siehe dazu Abbildung 3.3).
Kennlinie und Verhalten der Basis-Emitter-Strecke
Zur Messschaltung: Der Transistor wurde in Basisschaltung verschaltet (die Basis wird über C2 wechselspannungsmäßig geerdet). Die Basisspannung wird so eingestellt, dass, bei einem Emitterwiderstand von 4,7 kΩ ein Emitterstrom von etwa 0,2 mA fließt. (Im Treblebooster fallen über dem Kollektorwiderstand RK von 10 kΩ etwa 2 V ab; somit fließt ein Kollektor- und Emitterstrom IE etwa 0,2 mA). In der Messschaltung ist der Kollektorwiderstand ist kleiner, um das Verhalten ohne Übersteuerung besser untersuchen zu können. Zur Ermittlung der statischen Kennlinie der Basis-Emitter-Strecke wird nunr der Emitterwiderstand von 1 kΩ bis auf 4,7 MΩ erhöht und jeweils die Emitterspannung gemessen und der zugehörige Emitterstrom berechnet. Daraus kann nun grob der differentielle Widerstand des Emittereingangs rE,Gleichsp. in Abhängigkeit vom Emitterstrom bestimmt werden.

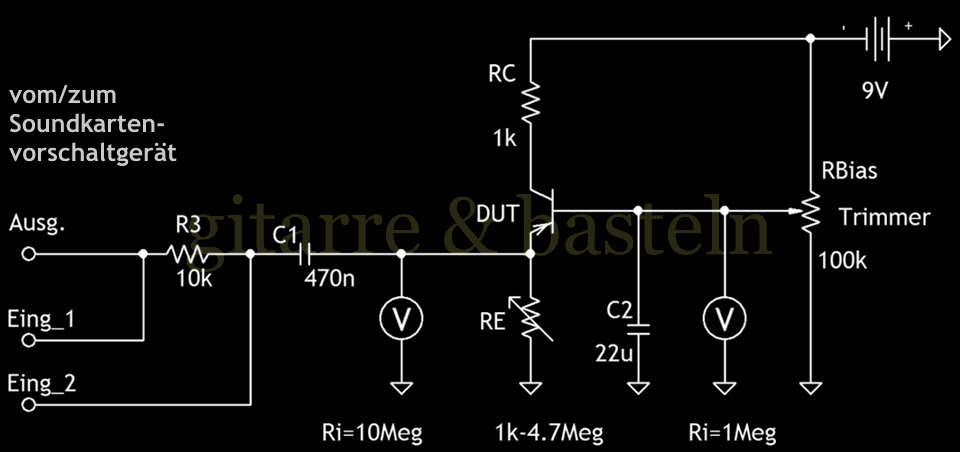
Abb. 3.3: Messschaltung zur Ermittlung des Verhaltens und der Parameter des Transistors, gemessen von Emitter. Das Messsignal von der Soundkarte hatte eine Frequenz von 1 kHz.
Weiterhin wurde die Messschaltung vor und nach einen Emittervorwiderstand R3 = 10 kΩ mit der Soundkarte des PC verbunden. Der Emittervorwiderstand und der differentielle Widerstand der Basis-Emitter-Strecke bilden so einen Signalspannungsteiler. Über diesen Signalspannungsteiler ein Sinussignal geleitet und auf weitgehende Verzerrungsarmut ausgepegelt und die Pegel gemessen. Aus dem Verhältnis der Spannungen vor und nach dem Vorwiderstand konnte der differentielle Emittereingangswiderstand rE,NF noch einmal genauer berechnet werden.
Für jede Messung wurde auch ein möglicher bzw. passender Emissionskoeffizient η bestimmt. Die Berechnungen von rE und η leiteten sich wie folgt ab:
- rE,NF
Der differentielle Emittereingangswiderstand rE kann aus dem Verhältnis der Spannungen beidseitig des Emittervorwiderstands R3, d. h. aus den beiden Signalspannungen uEing,1 und uEing,2 berechnet werden:
\( \begin{equation} r_{\textrm{E,NF}} = R_3\cdot \cfrac{ u_{\textrm{Eing,2}}} { u_{\textrm{Eing,1}} - u_{\textrm{Eing,2}} } \tag{1}\end{equation} \)
- rE,Gleichsp.
Hier wird der differentielle Emittereingangswiderstand rE als Quotient der Messwertänderungen von IE und UBE berechnet, allerdings werden die Änderungen in beide Richtungen (die zu den nächstgrößeren und den nächstkleineren Messwerten) in die Berechnung einbezogen – es wird das geometrische Mittel gebildet: Aus jeweils drei Einzelmessungen X, Y und Z lässt sich ableiten:
\( \begin{eqnarray} ΔU_{\textrm{1}} & = & U_{\textrm{BE,Y}} - U_{\textrm{BE,X}} \\~\\ ΔU_{\textrm{2}} & = & U_{\textrm{BE,Z}} - U_{\textrm{BE,Y}} \\~\\ ΔI_{\textrm{1}} & = & I_{\textrm{C,Y}} - I_{\textrm{C,X}} \\~\\ ΔI_{\textrm{2}} & = & I_{\textrm{C,Z}} - I_{\textrm{C,Y}} \\~\\ r_{\textrm{E,Y}} & = & \sqrt{\frac{ΔU_{\textrm{1}}\cdot ΔU_{\textrm{2}} } {ΔI_{\textrm{1}}\cdot ΔI_{\textrm{2}} } } \tag{2}\end{eqnarray} \)
- ηE,NF
Aus dem Zusammenhang zwischen differentiellem Emittereingangswiderstand und Emitterstrom kann die Größe des Emissionskoeffizienten η abgeschätzt werden. Ausgehend von der Shockley-Gleichung, die zunächst nach den Strömen umgestellt,
\( \begin{eqnarray} I_{\textrm{E}} & = & I_{\textrm{S}} \left( \exp{\left( \frac{U_{\textrm{BE}}} {\eta \cdot{}U_{\textrm{T}}} \right) }-1 \right) \\~\\ \frac{I_{\textrm{E}}+I_{\textrm{S}}} {I_{\textrm{S}}} & = & \exp{\left( \frac{U_{\textrm{BE}}} {\eta\cdot U_{\textrm{T}}} \right)} \tag{3}\end{eqnarray} \)
seitenvertauscht und logarithmiert,
\( \begin{equation} \cfrac{U_{\textrm{BE}}} {\eta{}\cdot{}U_{\textrm{T}}} = \ln\left( \cfrac{I_{\textrm{E}}+I_{\textrm{S}}} {I_{\textrm{S}}} \right) \tag{4}\end{equation} \)
und anschließend nach UD bzw. nach UBE umgestellt wird:
\( \begin{equation} U_{\textrm{BE}} = \eta{}\cdot U_{\textrm{T}}\cdot \ln\left( \cfrac{I_{\textrm{E}}+I_{\textrm{S}}} {I_{\textrm{S}}} \right) \tag{5}\end{equation} \)
Jetzt kann nach dem gemessenen Emitterstrom IE + IS abgeleitet werden, wodurch eine recht einfache Gleichung entsteht,
\( \begin{equation} r_{\textrm{BE}} = \eta\cdot U_{\textrm{T}}\cdot \cfrac{1} {I_{\textrm{E}}+I_{\textrm{S}}} \tag{6}\end{equation} \)
die nach η umgestellt wird, wonach diese Gleichung
\( \begin{equation} \eta{} = \cfrac{I_{\textrm{E}}+I_{\textrm{S}}} {U_{\textrm{T}}} \cdot{} r_{\textrm{BE}} \tag{7}\end{equation} \)
in die obige Gleichung 1 eingesetzt werden kann:
\( \begin{equation} \eta{} = R_3 \cdot\cfrac{I_{\textrm{E}}+I_{\textrm{S}}} {U_{\textrm{T}}} \cdot\cfrac{ u_{\textrm{Eing,2}}} { u_{\textrm{Eing,1}} -u_{\textrm{Eing,2}} } \tag{8}\end{equation} \)
- ηE,Gleichsp.
Auch dieser Zusammenhang zwischen den Änderungen von Ie und UBE und η leitet sich aus der Shockley-Gleichung ab, die hier zunächst nach ID + IS umgestellt wird:
\( \begin{eqnarray} I_{\textrm{D}} & = & I_{\textrm{S}}\cdot \left[ \exp \left( \cfrac{U_{\textrm{F}}} {\eta\cdot U_{\textrm{T}}} \right) -1 \right] \\~\\ I_{\textrm{D}} + I_{\textrm{S}} & = & I_{\textrm{S}}\cdot{} \exp \left( \cfrac{U_{\textrm{F}}} {\eta\cdot U_{\textrm{T}}} \right) \tag{9}\end{eqnarray} \)
Um aus der Änderung von Basis-Emitter-Spannung und Emitterstrom einen Wert für η ableiten zu können, wird die obige Gleichung 9 für jeweils verschiedene Werte von UBE und IE durch sich selbst dividiert
\( \begin{equation} \cfrac{I_{\textrm{D,1}}+I_{\textrm{S}}} {I_{\textrm{D,2}}+I_{\textrm{S}}} = \exp{\left( \cfrac{ U_{\textrm{BE,1}} - U_{\textrm{BE,2}} } {\eta\cdot U_{\textrm{T}}} \right)} \tag{10}\end{equation} \)
logarithmiert
\( \begin{equation} \ln{\left( \cfrac{I_{\textrm{D,1}}+I_{\textrm{S}}} {I_{\textrm{D,2}}+I_{\textrm{S}}} \right)} = \cfrac{ U_{\textrm{BE,1}} - U_{\textrm{BE,2}} } {\eta{}\cdot{}U_{\textrm{T}}} \tag{11}\end{equation} \)
und nach η aufgelöst:
\( \begin{equation} \eta = \cfrac{1} {U_{T}}\cdot{} \cfrac{ U_{BE,1} - U_{BE,2} } {\ln\left( \cfrac{I_{D,1}+I_{S}} {I_{D,2}+I_{S}} \right) } \tag{12}\end{equation} \)
Soweit die theoretischen Hintergründe. In – beispielsweise – EXCEL kann nun für jeden Emitterstrom IE ein passendes η berechnet und in einem Diagramm dargestellt werden. Durch Wahl eines geeigneten Festwertes für den Sperrstrom IS (im konkreten Fall I>S = 0,3 µA) kann die Darstellung hypothetisch so „hingebogen“ werden, dass η konstant und unabhängig vom Emitterstrom IE ist. Das heißt, für die Basis-Emitter-Strecke des untersuchten Transistors wurden IS und η grafisch ermittelt (siehe Abbildung 3.4).
Interessant ist, wie „sauber“ der Zusammenhang zwischen Basis-Emitter-Spannung, Emitterstrom und differentiellem Widerstand am Emittereingang dabei ist (einmal abgesehen von den Messfehlern bei Strömen um etwa 10 µA). Weiterhin fällt auf, dass der einigermaßen saubere logarithmische Zusammenhang zwischen Basis-Emitter-Spannung und Emitterstrom tatsächlich um einen Offset von etwa(!) 100 mV nach unten verschoben ist; für Emitterströme kleiner ≈ 20 µA wird die Basis-Emitter-Spannung (bei einem pnp-Transistor) positiv. Dieses Verhalten ist durch die germanium-typisch hohen Restströme bedingt. Da es hier vorrangig darum geht, das dynamische Verhalten der Basis-Emitter-Strecke nachzubilden, ist dieser Offset nicht problematisch.


Abb. 3.4: Zusammenhang zwischen dem Emitterstrom, dem differentiellen Emittereingangswiderstand rE, dem (gedachtem) Koeffizienten η sowie der Basis-Emitterspannung UBE nach Messung eines Transistors AC128 in einer Messschaltung entsprechend Abbildung 3.3.
Schaltungstechnische Umsetzung der Idee
Bei der Messung der Basis-Emitter-Strecke wurde also ermittelt, dass sich die Basis-Emitter-Strecke des Transistors wie eine Diode mit einem Emissionskoeffizienten η ≈ 1 und einem Sperrstrom IS kleiner 1 µA verhält, wenn auch mit einem Spannungs-offset von etwa 100 mV.
Ein praktischer Ersatz, d. h. eine schaltungstechnischer Ersatz für die Basis-Emitter-Strecke könnte in einer Schottky-Diode 1N5817 bestehen. Sie hat, nach Untersuchung des Autors, einen Emissionskoeffizienten η von etwa 1 und einen Sperrstrom IS von etwa 0,6 µA und hat in der Schaltung des Trebleboosters bei einem Emitterstrom von etwa 0,2 mA einen differentiellen Widerstand von etwa 130 Ω (rDiode = η⋅ UT / IE) Wenn der Stromverstärkungsfaktor des im Treblebooster verwendeten Transistors typischerweise zwischen 90 und 100 liegt, kann an der Basis mit einer Zunahme des Eingangswiderstands um 10 kΩ–13 kΩ (β⋅ rDiode) gerechnet werden.
Sollte das als Erhöhung des Eingangswiderstands zu wenig sein, so kann man auch zwei Dioden 1N5817 in Reihe schalten (mit einem „Gesamt-η“ von zwei) oder sich mit einer Siliziumdiode behelfen (η etwa 1,5). Um das begrenzte Ansteigen des differentiellen Widerstandes dieser Diode bei Strömen kleiner 1 µA nachzubilden („normale“ Dioden haben einen wesentlich geringeren Sperrstrom, da tritt dieser Effekt erst bei wesentlich geringeren Diodenströmen auf) kann die Diode vorgespannt werden – wie in der folgenden Abbildung 3.5 dargestellt:


Abb. 3.5: Simulation einer Siliziumdiode mit hohem Sperrstrom durch zwei vorgespannte Dioden (D1und D2) – die Erzeugung der Vorspannung erfolgt über D3 und, gegebenenfalls, über einen Widerstand parallel zu D4 anstelle des Kurzschlusses.
Die beiden linken Dioden D1 und D2 werden durch die Spannung, die auf der Diode D3 abfällt, vorgespannt. Die vierte Diode D4 wird nicht verwendet und kurzgeschlossen – allerdings bietet die Verwendung einer Graetzbrücke neben der einfachen Verschaltung der Dioden den Vorteil, dass alle drei benutzten Dioden die gleiche Temperatur haben, wodurch die Schaltung etwas stabilisiert wird. Beispielsweise führt eine Temperaturerhöhung nicht nur zu einer erhöhten Leitfähigkeit ((und zu einem geringeren differentiellen Widerstand der Dioden D1 und D2), sondern auch zu einer geringeren Spannung über D3 und somit auch über D1 und D2, wodurch erstgenannter Effekt abgeschwächt wird.
Zur Dimensionierung: Der differentielle Widerstand einer Diode ist in etwa reziprok zum Dioden(ruhe)strom, läuft aber bei sehr kleinen Strömen nicht gegen unendlich, sondern gegen η ⋅ UT / IS. Der Sperrstrom der 1N5817 wurde mit etwa 0,6 µA bestimmt und η mit 1, der maximale differentielle Widerstand liegt so bei etwa 40 kΩ.
Soll die Schaltung in Abbildung 3.5 bei einem Emitterstrom gegen null einen maximalen differentiellen Widerstand von 40 kΩ haben, so müssen die Dioden D1 und D2 jeweils auf einen differentiellen Widerstand von 80 kΩ vorgespannt werden. Dafür ist entsprechend der vom Autor ermittelten Kennlinie der Dioden (siehe Abbildung 3.6) eine Vorspannung von etwa 0,31 V pro Diode notwendig. Eine Spannung von 2⋅0,31 V = 0,62 V über D1 und D2 bzw. über D3 wird mit einem Strom von etwa 1,2 mA durch D3 erreicht, woraus sich für R1 ein Wert von 6,8 kΩ ergibt.

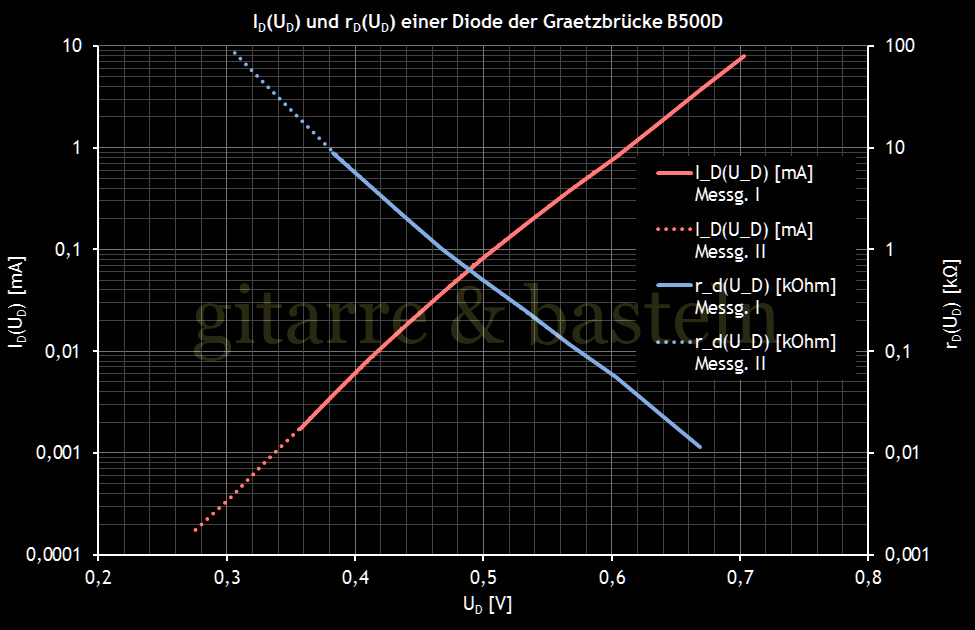
Abb. 3.6: Zusammenhang zwischen der Diodenruhespannung und dem Diodenruhestrom sowie dem differentiellen Widerstand einer Diode der Graetzbrücke B500D.
(Sollte, bei einer anderen Dimensionierung oder einer anderen Graetzbrücke, die Vorspannung über D3 zu klein sein, kann der Kurzschluss parallel zu D4 auch durch einen Widerstand ersetzt werden, so dass D4 einen Teil der Vorspannungserzeugung für D1 und D2 übernimmt.)
Nachrechnen mit EXCEL
Um den beiden Ideen dieses Abschnitts – der Nachbildung der Basis-Emitter-Strecke einer Germaniumtransistors durch eine Schottkydiode bzw. zwei vorgespannten Gleichrichterdioden noch ein wenig zu verdeutlichen, und um zu untersuchen, ob sich ein pn-Übergang mit einem maximalen differentiellen Widerstand nicht einfacher durch die Parallelschaltung einer Diode mit einem Widerstand umsetzen lässt, wurden die gemessenen statischen Kennlinien des Transistors und der Dioden (Spannung gegen Strom und differentieller Widerstands gegen Strom) in einem Diagramm zusammengetragen (siehe Abbildung 3.7). Die Kennlinie der Parallelschaltung Diode und Widerstand wurde berechnet. Außerdem wurde mit dem Diagramm ein Wert für einen Widerstand RBahn = 39 Ω grafisch ermittelt. RBahn wird den beiden Diodenschaltungen jeweils in Serie zugeschaltet und bildet den Bahnwiderstand des zu simulierenden pn-Übergangs nach.

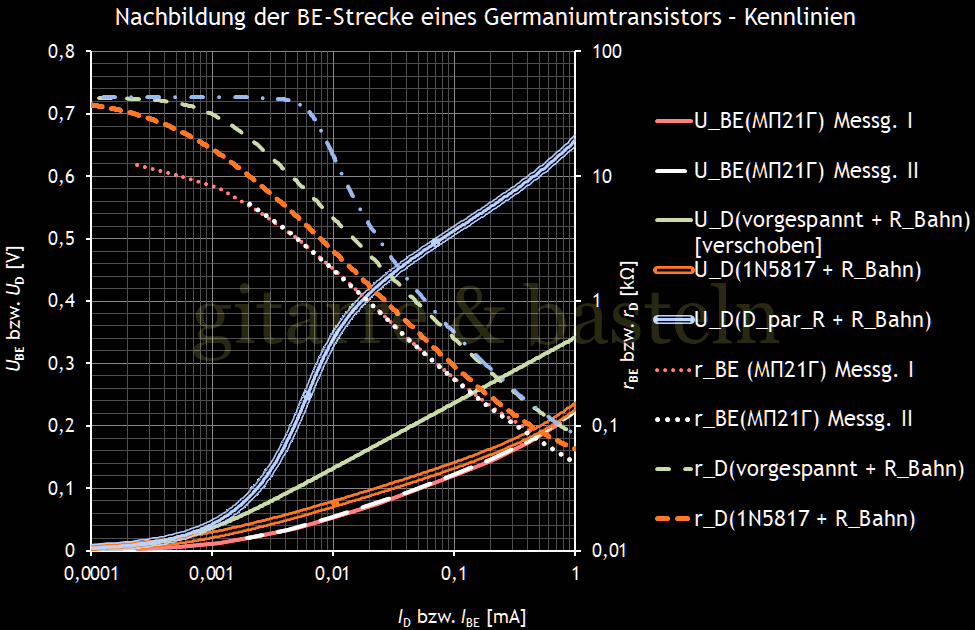
Abb. 3.7:
Statische Kennlinie der Basis-Emitter-Strecke eines Germaniumtransistors
МП21 (rot / schwarz; in zwei
Messungen aufgenommen)
und die berechnete Nachbildung dieser Kennlinie
mit Hilfe
– einer Siliziumdiode und eines Widerstands 43 kΩ parallel (blau),
– einer Schottkydiode 1N5817 (orange) sowie
– einer vorgespannten Siliziumdiode
(grün; Kennlinie
UD(ID)
um etwa 300 mV nach unten verschoben).
Zur Erläuterung: Die schwarzen und roten Graphen zeigen das statische Verhalten des untersuchten Germaniumtransistors anhand von jeweils zwei Messungen (UBE als Funktion von IBE – durchgehende Linie, sowie rBE als Funktion von IBE – Punktlinie).
Die orangefarbenen und grünen Graphen zeigen diese Kennlinie für eine Diode 1N5817 bzw. für die beschriebene Schaltung aus vorgespannten Dioden. Im Diagramm musste die grüne Strom-Spannungs-Kennlinie für die vorgespannte Diode der besseren Übersicht wegen um etwa 300 mV nach unten verschoben werden. Zur Erklärung: Die Diode wurde auf den halben Sperrstrom der Basis-Emitter-Strecke vorgespannt, d. h. auch dann, wenn kein Emitterstrom fließt, fällt über der Diode die entsprechende Spannung ab. Ingesamt bilden beide Schaltungen den Verlauf der Basis-Emitter-Spannung und des differentiellen Basis-Emitter-Widerstands (in unterschiedlicher Größe von differentiellem Widerstand und Diodespannung) recht gut nach.
Die blauen Graphen (dreifache Linie und Strichpunktlinie) zeigen die Kennlinien der Parallelschaltung einer Diode mit einem ohmschen Widerstand zur Begrenzung des maximalen differentiellen Widerstands. Dieser Ansatz liefert das schlechteste Ergebnis der Simulation, da der differentielle Widerstand der Parallelschaltung beim Übergang in den Cut Off sehr schnell zunimmt und die Spannung über Diode und Widerstand sehr schnell zusammenbricht. Hier ist mit einer ungünstigen Kennlinien-Verformung im Cut-Off-Bereich des Transistors zu rechnen.
Zwei Schaltungsvorschläge
Zum Abschluss dieses Teils des Artikels ein Schaltungsentwurf (ungetestet, bitte die fehlenden Hauptelkos dazudenken), der die beschriebenen Überlegungen zusammenfasst – der Entwurf ist als Vorschlag zur Modifikation der bekannten Rangemaster-Schaltung zu verstehen. Teil a) links zeigt die Modifikation u. a. mit einer Diode 1N5817 im Emitterzweig, Teil b) rechts die u. a. mit vorgespannten Dioden in einer Graetzbrücke.


Abb. 3.8: Ungetestete Schaltungsentwürfe für zwei Treblebooster mit Emitterdioden für einen erhöhten Eingangswiderstand und eine geringere Verstärkung – in Schaltung a) ist der Eingangswiderstand der Schaltung bei gleichem Transistor etwa doppelt so groß wie der des Rangemaster Trebleboosters in Schaltung b) etwa zweieinhalb- bis dreimal. Die beiden Kondensatoren parallel zur Graetzbrücke dienen dazu, Brummen und Rauschen aus der Vorspannung fü die Emitterdiode herauszufiltern.
Insbesondere die Werte für den Basisspanungsteiler sind nicht getestet, die Werte wurden so ausgewählt, dass die Basisruhespannung in gleichem Maße steigt wie die durch den größeren Emitterwiderstand und die zusätzlichen Bauelemente im Emitterkreis gestiegene Basisspannung, um den Emitterstrom und den Arbeitspunkt (die Kollektorruhespannung) nicht allzustark zu verändern. Die Basisspannungsteiler haben daher eine um etwa 1 V höhere Leerlaufspannung – beim Rangemaster etwa 1,1 V (9 V · 68 kΩ / (68 kΩ + 470 kΩ) bei Entwurf b) etwa 2,2 V (9 V · 220 kΩ / (220 kΩ + 680 kΩ); Entwurf a) entsprechend.
Außerdem soll der nun hochohmige Treblebooster auch einen entsprechend hochohmigen Basisspannungsteiler haben. Der Basisspannungsteiler, d. h. die Einspeisung des Basisstroms, hat beim originalen Rangemaster Treblebooster einen Quellwiderstand von 60 kΩ (68 kΩ parallel 470 kΩ), bei Schaltungsvorschlag a) etwa 110 kΩ und bei Schaltungsvorschlag b) 170 kΩ. Das entspricht in beiden Fällen der Erhöhung des differentiellen Widerstands an der Basis.
Der in diesem Abschnitt beschriebene Ansatz der Erhöhung des Eingangswiderstand wird im „Laboranhang“ C genauer untersucht.
