Übersetzte Fachartikel zur Pseudo-Trioden-Verzerrung von Viktor Kempf, AMT-Electronics
FET-Emulation von Triodenverzerrungen
Kapitelinhalt:[ Überspringen ]- Vorwort •
- Die Begrenzung durch die Vakuumtriode •
- Die Begrenzung in der Sourceschaltung mit Lastwiderstand •
- Pseudotrioden-Verzerrung mit FETs •
- Die Diode •
- JFET-basierter ENGL-Bogner •
- Fazit
Виктор Кемпф (Viktor Kempf, AMT-Electronics https://amtelectronics) © 2006
Vorwort
Viele kennen den Autor dieses Artikels als einen konsequenten Anhänger der Nutzung von Feldeffekttransistoren bei der Gitarrenverstärkung. Der Autor hat sich hier immer wieder mit unterschiedlichem Erfolg (vom Gesichtspunkt der Formung des traditionellen Gitarrentones) für den Einsatz von Feldeffekttransistoren eingesetzt. Beim Gitarrensound geht es bekanntlich zuerst um die Formung des Signalspektrums mittels Verstärkung und der Begrenzung. Traditionell wird angenommen, dass nur Röhrenverzerrungen dem Gitarrensignal die spezifische Klangfarbe geben können, die von den Gitarristen und den wahren Liebhabern der Gitarrenmusik geschätzt wird. Nichtsdestotrotz, ungeachtet des wesentlichen Unterschiedes der Ausgangskennlinie von Feldeffekttransistoren und Vakuumtrioden, ist es gelungen, FETs dazu zu bringen (Signale) wie eine Röhre zu begrenzen, auch wenn dazu einen langer Weg voll der Fehler, Enttäuschungen und Überraschungen zurückgelegt werden musste.
Die Begrenzung durch die Vakuumtriode
Wir betrachten (am Beispiel der verbreiteten Triode 12AX7), wie das Signal die Vakuumtriode ins Cliping treibt. Am Eingang liegt ein Sinussignal von 20 V (Spitze-Spitze) an. Die obere Halbwelle wird am Gitter vom Niveau UК (UК – das Spannungspotential der Kathode gegen Masse) begrenzt.
Bei der Überschreitung der Spannung zwischen dem Gitter und der Kathode fließt ein Strom. So kann man die Triode eingangsseitig wie eine Vakuumdiode betrachten, die zwischen dem Gitter und der Kathode angeschlossen ist (siehe Abb. 1).


Abb. 1: Die Begrenzung der positiven Halbwelle am Gitter (UК = 1,8 V).
Natürlich, das ist seit langem bekannt und nichts Neues für die Menschheit. Beim normalen Einsatz der 12AX7 führt der Kathodenwiderstand von 1–3 kΩ zu einer Begrenzung der oberen Halbwelle des Eingangssignals bei etwa 2 V.
Das Signal auf der Anode ist das invertierte und um KU (den Spannungsverstärkungsfaktor der Stufe) verstärkte Eingangssignal der Verstärkerstufe (siehe Abb. 2).

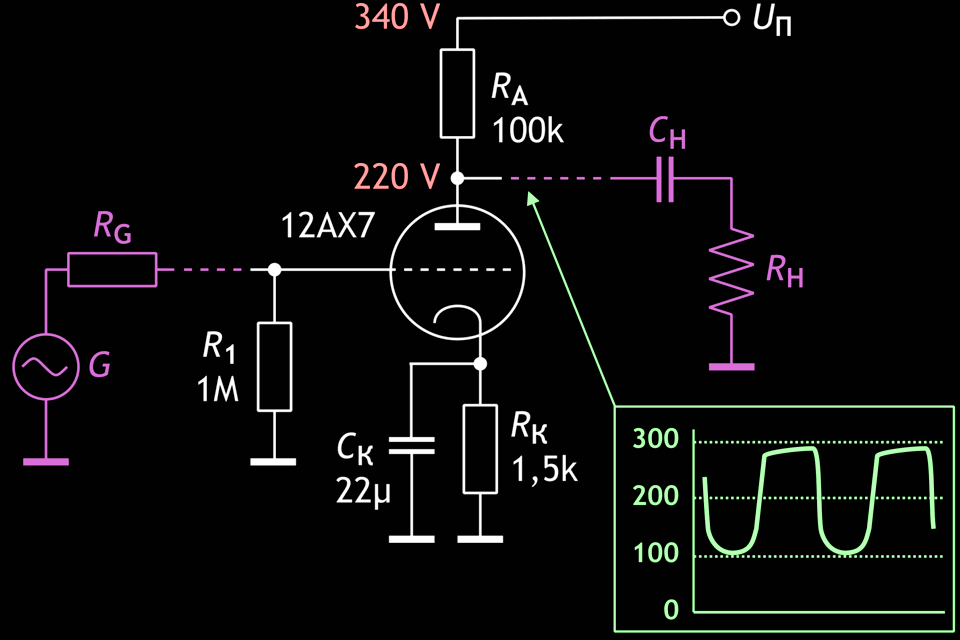
Abb. 2: Typische Verstärkerstufe mit einer Triode 12AX7.
Die Verstärkung der Stufe:
\( \begin{eqnarray} K_{\textrm{U}} & = & S \cdot{} (R_{\textrm{А}}\,||\, r_{\textrm{А}}\,||\, R_{\textrm{H}}) ~~~\textrm{mit} \\ r_{\textrm{А}} & = & \mathit{µ} × S \tag{1}\end{eqnarray} \)
μ – die Spannungsverstärkung der Triode;
S – die Steilheit;
RА – der Anodenwiderstand;
rА – der Innenwiderstand der Anode;
RH – der Lastwiderstand.
KU hängt ab vom Innenwiderstand der Triode rА (gewöhnlich 50 bis 60 kΩ). Ohne Belastung hat die Stufe einen Verstärkungsfaktor von etwa 65.
Betrachten wir nun für beide Halbwellen das Signal auf dem Ausgang.
Bei Verstärkung der oberen Halbwelle kann die Anodenspannung nicht endlos zunehmen, die Röhre sperrt. In diesem Fall hängt das Maximum der positiven Halbwelle am Ausgang vom Verhältnis RА zu RH ab, die gewöhnlich einen Spannungsteiler bilden.
Ohne Belastung wird die obere Halbwelle das Niveau der Betriebsspannung 340 V erreichen. Bei Belastung (zum Beispiel 200 kΩ) wird die obere Halbwelle nur 280 V erreichen. Im Endeffekt haben wir ein Signal, wie es in Abb. 3 dargestellt wird (die Neigung des Gipfels der oberen Halbwelle wird durch das Umladen des Koppelkondensators CN bewirkt und hängt von dessen Kapazität ab).

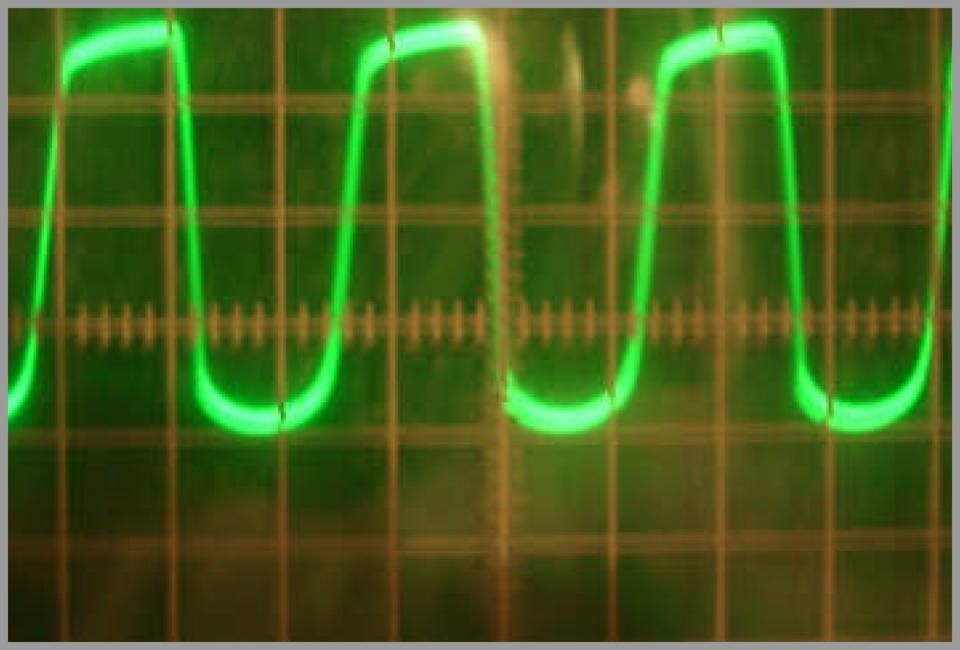
Abb. 3: Das Oszillogramm des realen Signals an der Anode (50 V / Teilung) (Oszillogramm und Foto: AMT-Electronics).
Die untere Halbwelle in dieser Zeichnung ist nichts anderes als die um KU verstärkte begrenzte positive Eingangshalbwelle. Da die „Eingangsdiode“ der Triode die positive Halbwelle am Eingang bei 2 V begrenzt, weist die untere Halbwelle des Signals an der Anode das charakteristischen Diodencliping (wörtlich: diodenartige Abrundung) auf. (In unseren Fall ist die Spannungsverstärkung KU gleich 55, d. h. das Signal „rundet sich ab“ bei einer Anodenspannung von 220 V (Arbeitspunkt) - 2 V ⋅ 55 = 110 V).
Ausgangsseitig begrenzt die Triode nur die obere Halbwelle. Daraus ergibt sich die Notwendigkeit einer ausreichend hohen Anodenspannung für diese Verstärkerstufe. Wird die Versorgungsspannung der Stufe nach Abb. 2 unter 220 V verringert, so wird das Ausgangssignal der Stufe auch ausgangsseitig an der unteren Halbwelle (über das verstärkte Eingangscliping hinaus) beschränkt, was zur einer heftigen Verschlechterung des Wohlklanges (благозвучность: благо gut; звучность Klangfülle) der Verzerrungen führen wird. Das ist der Grund dafür, dass die Röhre bei herabgesetzter Anodenspannung nicht „klingt“.
Anmerkung: Bei herabgesetzter Anodenspannung gibt es immer die Möglichkeit, entweder den Wert des Anodenwiderstands oder den Anodenstrom durch die Vergrößerung des Kathodenwiderstands zu verringern, damit der Arbeitspunkt die „normale Lage“ von 55 … 65 % der Speisespannung einnimmt.
Die Triode begrenzt also jeweils nur die positive Halbwelle, am Gitter wie auch an der Anode.
Die Begrenzung in der Sourceschaltung mit Lastwiderstand
Der FET (es handelt sich aufgrund des Silizium-pn-Übergangs um einen n-Kanal-FET) stellt auch eine Diode dar und begrenzt die obere Halbwelle des Eingangssignals. Der Level der Begrenzung bildet dabei die Summe Upn + Us, wobei Upn für den Spannungsabfall über dem Silizium-(pn)-Übergang und US für die Sourcespannung steht.

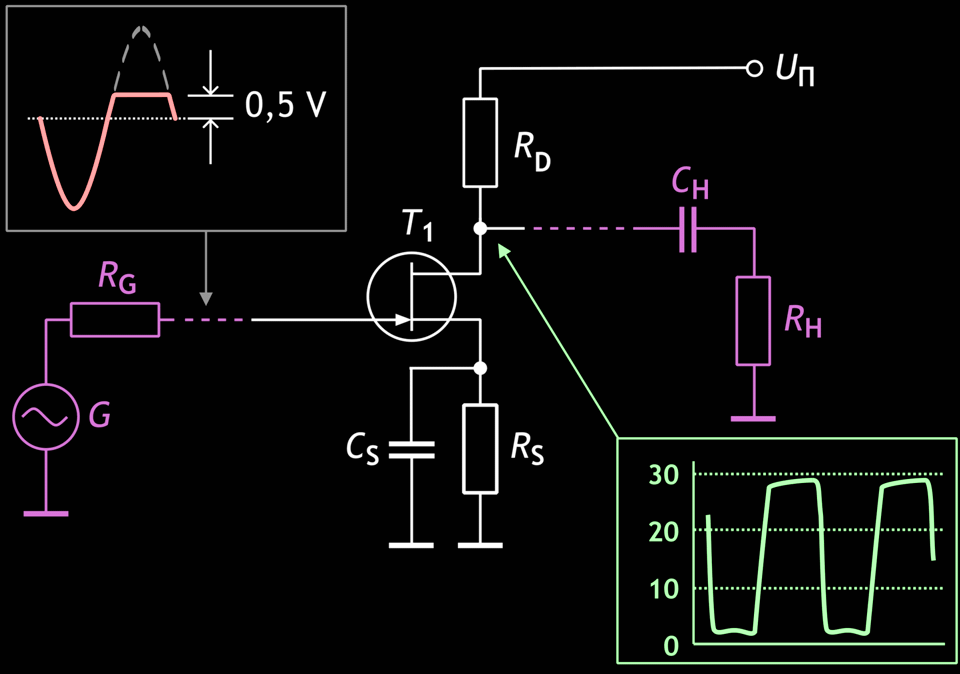
Abb. 4: Die Verstärkerstufe mit den Begrenzungen am Eingang und nach dem Ausgang.
Das Problem des FET in Sourceschaltung mit einem Lastwiderstand besteht darin, dass das Signal am Ausgang nicht nur an der oberen Halbwelle (wie bei der Vakuumtriode) begrenzt wird, sondern dass auch die untere Halbwelle am Ausgang begrenzt wird, bevor die Begrenzung am Eingang (durch den oben genannten pn-Übergang) wirksam werden kann (siehe Abb. 4). Wenn die Eingangsdiode leitend wird und so die Eingangsspannung begrenzt wird, ist der FET bereits in der Sättigung, und der Eingangsstrom durch die Diode speist sich aus dem Strom durch den Kanal. Dieser bildet auf der unteren Halbwelle den sogenannten inversen Ausschnitt (die unten begrenzte Halbwelle wird wieder nach oben „eingestülpt“). Dieser Effekt kann durch Vorschalten eines Gatewiderstandes (400 kΩ–1 MΩ) abgeschwächt werden. Aber das löst das eigentliche Problem nicht, dass der FET das Signal bereits ausgangsseitig begrenzt, bevor die Begrenzung durch den pn-Übergang am Gate wirksam wird, so dass mit dem FET in dieser Schaltung kein Röhrenklang möglich ist. Ein Versuch, die „untere“ Begrenzung zu verbessern, war die Kaskodenschaltung des FETs. Aber leider muss festgestellt werden, dass – selbst bei einer gewissen Ähnlichkeit der Form des Ausgangsignals bei geringer Aussteuerung – bei der Übersteuerung des Eingangs auch hier dieselben Probleme auftreten. Dieses Problem betrifft gleichermaßen alle Verstärkerstufen in Sourceschaltung einschließlich der µ-Schaltung (Übersetzer: gemeint sind wohl µ-Amps). Außerdem bietet die µ-Schaltung nicht die „obere“ Begrenzung durch den Strom, was uns eher vom Röhrenklang fortführt, als das wir uns ihm nähern. Letztendlich sprach man sogar von FET-Sound.
Anmerkung: Die µ-Schaltungen mit Vakuumtrioden (SRPP) klingen, nach Meinung des Autors, in der Übersteuerung aus demselben Grund nicht: die Begrenzung der oberen Halbwelle ist nicht durch den (Gitter-)Strom bedingt.
Pseudotrioden-Verzerrung mit FETs
Zunächst wissen wir, wie sich die Signalbegrenzung in einer Röhrenstufe darstellt und warum eine Stufe mit FET nicht in gleicher Weise das Signal begrenzt. Das Hauptproblem besteht darin, dass der relative Pegel der eingangsseitigen Begrenzung beim FET wesentlich höher ist.
Versuchen wir nun, dieses Problem zu lösen.
-
Erstens: Unter Berücksichtigung des Verhältnisses zwischen Betriebsspannung und dem eingangsseitigem Begrenzereinsatz (250 … 350 V gegenüber 2 V), sollte der FET mit einer hohen Betriebsspannung versorgt werden, was die Nutzung von Geräten mit niedriger Spannung ausschließt.
-
Zweitens wird für die eingangsseitige Begrenzung eine Germaniumdiode oder eine Schottky-Diode benutzt und diese dem PN-Übergang des FETs parallelgeschaltet.
-
Drittens muss die Verstärkung so gewählt werden, dass die Begrenzung der positiven Halbwelle am Eingang, multipliziert mit dem Verstärkungsfaktor der Stufe, garantiert nicht unter der Begrenzung der negativen Halbwelle am Ausgang liegt.
Dies geschieht am einfachsten durch einen zusätzlichen Sourcewiderstand.
Die Abbildung zeigt eine FET-Stufe, die alle diese Anforderungen erfüllt.

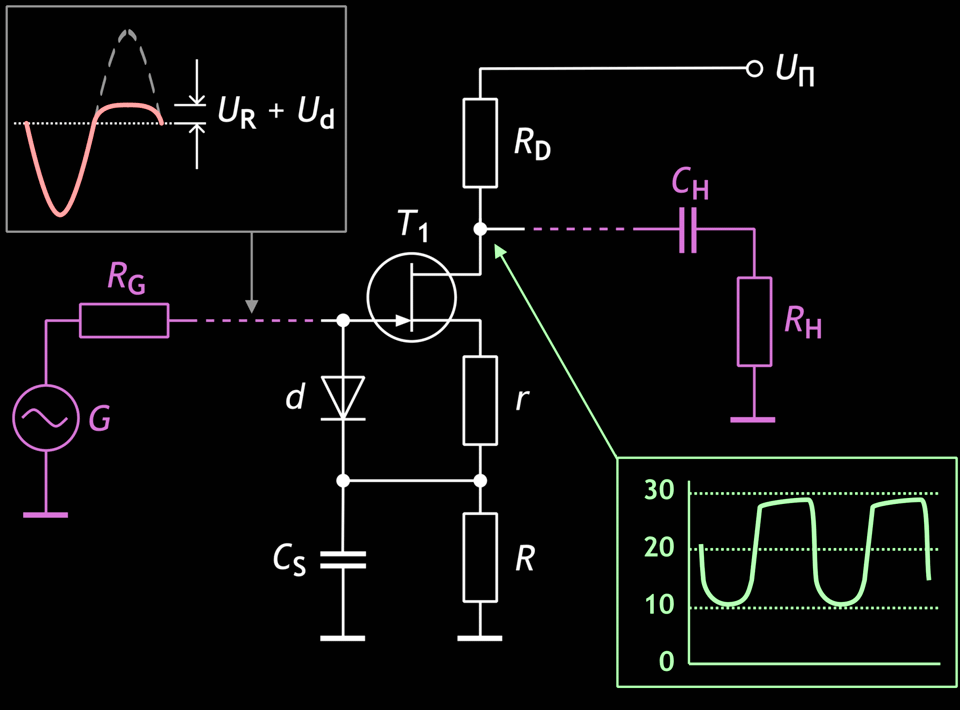
Abb. 5: Stufe in Sourceschaltung mit „Trioden“-typischer Begrenzung.
Wenn auch die Ausführung ersten beiden Bedingungen unkritisch ist, so fordert die dritte Bedingung wegen der Parameterstreuung des FET die Berechnung der Sourcewiderstände R und r, ausgehend von der Abschnürspannung Uco und dem Anfangssourcestrom IDSS des konkreten FETs.
Im Folgenden der mathematische Teil, den die Ungeduldigen überspringen können. (Zum Öffnen und Schließen klicken)
Der zu berechnende Gesamtwiderstand im Sourcekreis bestimmt die Lage des Arbeitspunkts, der sich aus der Berechnung UA = 2 / 3 ⋅ UП ergibt. (Real verschiebt sich der Arbeitspunkt mit dem Sperrstrom der Germaniumdiode um 1 … 3 V nach unten.)
\( \begin{eqnarray} R_{\sum} & = & (R + r) = \frac{U_{\textrm{S}}}{I_{\textrm{D}}} \\~\\ & = & \frac{-U_{\textrm{CO}}}{I_{\textrm{DSS}}} \left( 1 - \sqrt{\frac{I_{\textrm{D}}} {I_{\textrm{DSS}}} }\, \right) ~~\textrm{mit}~~I_{\textrm{D}}~–~Drainstrom \tag{2}\end{eqnarray} \)
Mit ID ≈ UП/(3⋅RD) (Anmerkung Übersetzer: auf dem Drainwiderstand soll ein Drittel der Betriebsspannung abfallen) ist der Gesamtwiderstand im Sourcekreis:
\( \begin{equation} R_{\sum} = - \cfrac{3\left( -U_{\textrm{CO}} \right)\cdot{} R_{\textrm{D}}} {U_П} \left( 1 - \sqrt{ \cfrac{U_П} {3\cdot{} R_{\textrm{D}}\cdot{} I_{\textrm{DSS}} } }\, \right) \tag{3}\end{equation} \)
Der Koeffizient der Verstärkung der Stufe (ohne Berücksichtigung der Steilheit des FET):
\( \begin{equation} K_{\textrm{U}} = \cfrac{R_{\textrm{D}}}{r_{\textrm{К}} + r} \tag{4}\end{equation} \)
mit rК – Kanalwiderstand des FET entsprechend der Formel:
\( \begin{equation} r_{\textrm{k}} = \cfrac{-U_{\textrm{CO}}} {2\cdot{} \sqrt{ I_{\textrm{DSS}}\cdot{} I_{\textrm{D}} } } \approx \cfrac{-U_{\textrm{CO}}} {2\cdot{} \sqrt{ \cfrac{U_П} {3\cdot{}R_{\textrm{D}}} \cdot{} I_{\textrm{DSS}} } } \tag{5}\end{equation} \)
Nehmen wir an, dass die maximal zulässige Amplitude der unteren Halbwelle am unbelasteten Ausgang gleich UП / 2 ist (unter Berücksichtigung der möglichen Arbeitspunktverschiebung aufgrund des Sperrstromes der Diode D ist das eine vollkommen vernünftige Entscheidung).
Dann sieht die dritte Bedingung mathematisch wie folgt aus:
\( \begin{equation} K_{\textrm{U}} × (U_{\textrm{d}} + U_{\textrm{r}}) = \cfrac{U_П}{2} \tag{6}\end{equation} \)
Unter Berücksichtigung der Formel für die Berechnung von KU und unter Berücksichtigung von
\( \begin{equation} U_{\textrm{r}} = I_{\textrm{D}}\cdot{}r = \cfrac{U_П\cdot{}r} {3\cdot{} R_{\textrm{D}} } \tag{7}\end{equation} \)
kommen wir zum Gleichungssystem:
\( \begin{equation} \cfrac{R_{\textrm{D}}} {r_{\textrm{К}} + r} \left( U_{\textrm{d}} + \cfrac{U_П\cdot{}r} {3\cdot{}R_{\textrm{D}}} \right) = \cfrac{U_П}{2} \tag{8} \end{equation} \)
und
\( \begin{equation} R_{{\sum}} = -U_{\textrm{CO}}\cdot{} \cfrac{3\cdot{}R_{\textrm{D}}}{U_П} \left( 1-\sqrt{ \cfrac{U_П} {3\cdot{}R_{\textrm{D}}\cdot{}I_{\textrm{DSS}}} } \right) \tag{9} \end{equation} \)
Eine Lösung dieses Systems ist:
\( \begin{equation} r = \cfrac{6}{5} \left( U_{\textrm{d}}\cdot{}\cfrac{R_{\textrm{D}}}{U_П} - \cfrac{R_{\sum}}{3} + \cfrac{r_{\textrm{К}}}{2} \right) \tag{10}\end{equation} \)
(Anmerkung Übersetzer: In diese Formel scheint ein Vorzeichenfehler eingeschlichen zu haben: Vertauscht man, wie auch im Originalartikel weiter unten in Gleichung 13, die Vorzeichen vor R∑ und rК, so erhält man auch positive Werte für r.)
\( \begin{equation} r = \cfrac{6}{5} \left( U_{\textrm{d}}\cdot{}\cfrac{R_{\textrm{D}}}{U_П} + \cfrac{R_{\sum}}{3} - \cfrac{r_{\textrm{К}}}{2} \right) \tag{10a}\end{equation} \)
(Für diesen mathematischen Teil können wir die Berechnungen abschließen.)
Damit können wir die Werte der Widerstände im Sourcekreis in vier Rechenschritten ermitteln. Die beiden ersten Schritte sind Hilfsrechnungen, Schritt 3 und 4 führen zum Ergebnis.
Der 1. Schritt. Die Berechnung des Gesamtsourcewiderstands:
\( \begin{equation} R_{\sum} = - U_{\textrm{CO}}\cdot{} \cfrac{3\cdot{}R_{\textrm{D}}} {U_П} \left(1 - \sqrt{ \cfrac{U_П} {3\cdot{}R_{\textrm{D}}\cdot{}I_{\textrm{DSS}}}} \right) \tag{11}\end{equation} \)
Der 2. Schritt. Die Berechnung des Kanalwiderstands des FET:
\( \begin{equation} r_{\textrm{К}} = \cfrac{-U_{\textrm{CO}}}{2} \cdot \sqrt{ \cfrac{3\cdot{}R_{\textrm{D}} } {U_П\cdot{}I_{\textrm{DSS}} } } \tag{12}\end{equation} \)
Der 3. Schritt. Die Berechnung des oberen Widerstands im Sourcekreis:
\( \begin{equation} r = \cfrac{6}{5} \left( U_{\textrm{d}}\cdot{}\cfrac{R_{\textrm{D}}}{U_П} + \cfrac{R_{\sum}}{3} - \cfrac{r_{\textrm{К}}}{2} \right) \tag{13}\end{equation} \)
Der 4. Schritt. Die Berechnung des unteren Widerstands im Sourcekreis:
\( \begin{equation} R_{\textrm{S}} = R_{\sum} - r \tag{14}\end{equation} \)
Die Diode
Eine Besonderheit der Stufe ist die Nutzung einer Diode mit geringem Spannungsabfall in Durchlassrichtung.
Die vergleichende Analyse der Anwendung von Schottky- und Germaniumdioden hat, wegen des Klanges der Germaniumdioden, eine deutliche Überlegenheit der Germaniumdioden gezeigt, die eine weichere Kennlinie haben.
Dabei muss man anerkennen, dass die Experimente nicht die komplexen Eigenschaften (die ganzen Vielfalt) der Schottky-Dioden berücksichtigen konnten. Es ist durchaus möglich, dass einige Metall-Halbleiter-Paare nicht schlechter als Germanium klingen werden.
Der Diodenstrom und der Spannungsabfall über die Diode stehen über die Ebers-Moll-Gleichung in Beziehung zueinander:
\( \begin{eqnarray} I_{\textrm{d}} & = & I_{\textrm{d,0}} \left( \exp{ \left( \frac{U_{\textrm{d}}} {U_{\textrm{T}}} \right) - 1 } \right) ~~\textrm{mit}~~ \\~\\ U_{\textrm{T}} & = & \frac{k\cdot{}T}{q} \approx 0{,}025\,\textrm{V} ~~\textrm{und}~~ \\~\\ I_{\textrm{d,0}} & - & \textrm{der Sättigungsstrom} \tag{15}\end{eqnarray} \)
Bei der Auswahl der Dioden muss man in erster Linie den Sperrstrom der Diode beachten. (Dabei nähert sich der Sperrstrom bei Vergrößerung der Gegenspannung asymptotisch dem Sättigungsstrom).
Von den einheimischen Dioden verfügen die Dioden Д18 und 1Г507А über einen kleinen Sättigungsstrom. Die Dioden einer Serie Д9 verlangen eine sorgfältige Auswahl.
Direkte Messungen des Sättigungstromes sind schwierig, aber indirekt kann man die Größe dieses Stromes über die Messung des Widerstands der Diode in Sperrrichtung beurteilen:
\( \begin{equation} I_{\textrm{d,0}} \approx \cfrac{U_Ω}{R_{\textrm{d}-}} \tag{16}\end{equation} \)
mit UΩ als der Spannung über einem Ohmmeter. (Die Diode wird in Sperrrichtung mit einem Ohmmeter gemessen, parallel dazu wird über ein Voltmeter die Spannung gemessen, die gewöhnlich bei 0,3 bis 0,5 V liegt.)
Anmerkung: Bei der Auswahl der Dioden wird empfohlen, nur Exemplare mit einem „Sperrwiderstand“ von mehr als 500 kΩ zu verwenden.
Für den Strom durch die Diode zur Zeit der maximalen Begrenzung kann man voraussichtlich annehmen:
\( \begin{equation} I_{\textrm{d}} \approx \cfrac{U_П}{4\cdot{}R_{\textrm{G}}} \tag{17}\end{equation} \)
Unter Berücksichtigung der nachfolgenden Logarithmierung und einiger Abweichungen vom Ideal, wie sie in verschiedenem Umfang allen pn-Übergängen eigen sind, sind solche Einschätzungen auch bei der ungefähren Berechnung vollkommen zulässig.
In dieser Weise hängt der Spannungsabfall über der Diode von der Größe des hinzugefügten Gatewiderstands RG ab und wird, bei einer gegebenen Betriebsspannung UП, für einige Diode mit bekannten Sperrwiderstand Rd− in etwa mit der Formel
\( \begin{equation} U_{\textrm{d}}\,[\textrm{V}] \approx \cfrac{1}{40}\cdot{} \ln{ \left( U_П\,[\textrm{V}]\cdot{} \cfrac{R_{\textrm{d}-}} {R_{\textrm{G}}} \right) } \tag{18}\end{equation} \)
beschrieben.
Anmerkung Übersetzer: (Öffnen und Schließen mit Mausklick)
Der obigen Gleichung 18 wurden Verweise auf die Einheit der Spannung beigefügt – aus einer Spannung lässt sich kein Logarithmus ableiten.
Ein wenig plausibler scheint die Gleichung:
\( \begin{eqnarray} U_{\textrm{d}} & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}\cdot{}I_{\textrm{d,0}}} \right) } \tag{18.a}\end{eqnarray} \)
bzw., wenn man für UT mit 25 mV der Einfachheit halber 1 / 40 V setzt:
\( \begin{eqnarray} U_{\textrm{d}}\,[\textrm{V}] & \approx & \frac{1}{40}\cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}\cdot{}I_{\textrm{d,0}}} \right) } \\~\\ && \textrm{mit:}~~ U_{\textrm{T}}\,[V] = 0{,}025\,\textrm{V} = \frac{1\,{\textrm{V}}}{40} \tag{18.b}\end{eqnarray} \)
Diese Gleichung lässt sich wie folgt herleiten:
\( \begin{eqnarray} I_{\textrm{d}} & = & I_{\textrm{d,0}} \left( \exp{ \left( \frac{U_{\textrm{d}}}{U_{\textrm{T}}} \right) - 1 } \right) \\~\\ \frac{I_{\textrm{d}}+I_{\textrm{d,0}}} {I_{\textrm{d,0}}} & = & \exp{ \left( \frac{U_{\textrm{d}}}{U_{\textrm{T}}} \right) } \\~\\ U_{\textrm{d}} & = & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{I_{\textrm{d}}} {I_{\textrm{d,0}}} + 1 \right) } \\~\\ & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{I_{\textrm{d}}} {I_{\textrm{d,0}}} \right) } \tag{18.c}\end{eqnarray} \)
Zusammen mit Gleichung 17 ergibt sich dann:
\( \begin{eqnarray} U_{\textrm{d}} & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}\cdot{}I_{\textrm{d,0}}} \right) } \tag{18.d}\end{eqnarray} \)
Wenn man jetzt allerdings annimmt, dass die am Ohmmeter gemessene Spannung UΩ etwa gleich 250 mV ist (was in etwa so belastbar ist wie die Annahme, dass Id in etwa gleich UП / 4 ⋅ RG ist), dann wird die etwas merkwürdige Gleichung 18 plausibel:
\( \begin{eqnarray} U_{\textrm{d}} & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}\cdot{}I_{\textrm{d,0}}} \right) } \\~\\ & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}} \cdot{} \frac{1} {I_{\textrm{d,0}}} \right) } \tag{18.e}\end{eqnarray} \)
Mit Gleichung 16 ergibt sich:
\( \begin{eqnarray} U_{\textrm{d}} & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}} \cdot{} \frac{R_{\textrm{d-}}} {U_{\textrm{Ω}}} \right) } \\~\\ & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{}R_{\textrm{G}}} \cdot{} \frac{R_{\textrm{d-}}} {0{,}25\,{\textrm{V}}} \right) } \\~\\ & \approx & U_{\textrm{T}} \cdot{} \ln{\left( \frac{U_П} {4\cdot{}0{,}25\,{\textrm{V}}} \cdot{} \frac{R_{\textrm{d-}}} {R_{\textrm{G}}} \right) } \\~\\ U_{\textrm{d}} & \approx & U_{\textrm{T}} \cdot{} \ln{\left( U_П\,[\textrm{V}] \cdot{} \frac{R_{\textrm{d-}}} {R_{\textrm{G}}} \right) } \tag{18.f}\end{eqnarray} \)
Für eine „Faustformel“ zur Bestimmung der ungefähren Diodenspannung ist das tatsächlich genau genug – eine Abweichung von 30 % bis 40 Prozent der „Ohmmeterspannung“ UΩ würde sich mit dem Logarithmus der Abweichung, multipliziert mit 25 mV, im Ergebnis auswirken.
Soweit die Anmerkung des Übersetzers.
Eine gute Alternative zur Germaniumdiode sind Germanium-HF-Transistoren in Diodenschaltung (der Kollektor ist mit der Basis verbunden, siehe Abb. 6): П416, П417, П422, ГТ309, ГТ322, ГТ346 u.a.

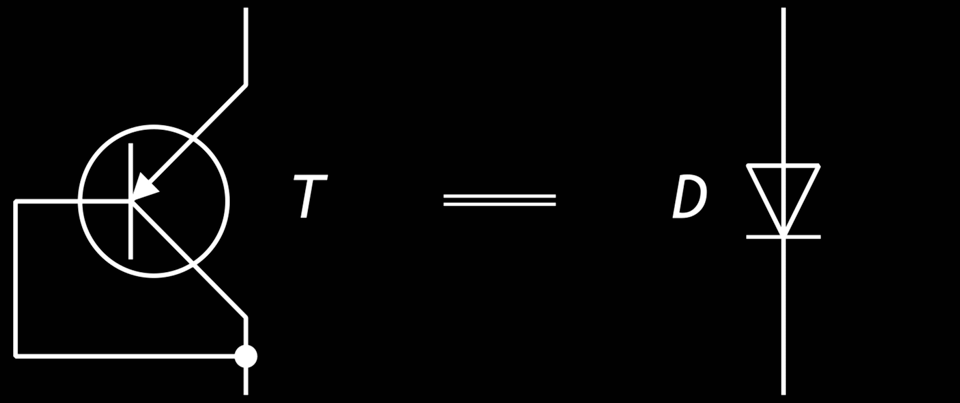
Abb. 6: Der pnp-Transistor in Diodenschaltung.
Für bipolare Transistoren in Diodenschaltung ergibt sich für den Spannungsabfall ungefähr:
\( \begin{eqnarray} U_{\textrm{d}}\,[\textrm{V}] & \approx & \frac{1}{40}\cdot{} \ln{ \left( U_П\,[\textrm{V}]\cdot{} \cfrac{R_{\textrm{d}-}} {\beta\cdot{}R_{\textrm{G}}} \right) } \tag{19}\end{eqnarray} \)
Anmerkung Übersetzer: (Öffnen und Schließen mit Mausklick)
Hier würde sich obige Gleichung 19 entsprechend verändern zu:
\( \begin{eqnarray} U_{\textrm{d}} & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{} R_{\textrm{G}}\cdot{} I_{\textrm{d,0}}\cdot{} β } \right) } \\~\\ & \approx & U_{\textrm{T}} \cdot{} \ln{ \left( \frac{U_П} {4\cdot{} R_{\textrm{G}}\cdot{} I_{\textrm{d,0}} } \right) } - U_{\textrm{T}} \cdot{} \ln{\left(β\right)} \tag{19.a}\end{eqnarray} \)
Für die Germanium-HF-Transistoren kann bei den kleinen Strömen und Kollektor-Emitter-Spannungen β mit 10 angenommen werden.
Im Falle eines Germaniumtransistors in Diodenschaltung entsteht gewöhnlich ein Spannungsabfall von 0,07 … 0,1 V; mit gewöhnlichen Germaniumdioden – 0,1 … 0,15 V.
Anmerkung: Meistens kann man für die Berechnungen von Ud gleiche Werte von 0,1 Volt annehmen (sowohl für die Germaniumdioden, als auch für Germaniumtransistoren).
JFET-basierter ENGL-Bogner
Kapitelinhalt:[ Überspringen ]- Formierung des Amplitudengangs •
- Auswahl der Verstärker der Stufen •
- Schaltung des Highgain-Preamps (Lead-Kanal)
Als „Versuchskaninchen“ wurde die Preamp-Schaltung „Engl-Mod2“ von Aznaur Gishyan (http://www.azg.spb.ru/azgschemes/azg-engl-mod2.gif) ausgewählt.
Anmerkung des Übersetzers: Da die Schaltung des Röhrenverstärkers unter der angegebenen Adresse nicht mehr zu finden war, wurde ein auf der Seite guitar-gear.ru gefundener Schaltplan nachgezeichnet – beschränkt auf den LEAD-Kanal.

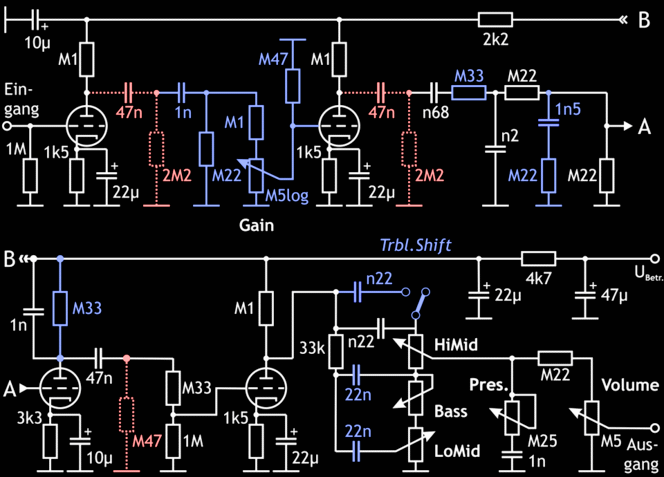
Abb. 7a: Schaltung der Vorstufe des von Aznaur Gishyan modifizierten ENGL-Verstärkers – die rot-gestrichelt gezeichneten Bauelemente dienen lediglich der Kanalumschaltung im Röhrenverstärker, die blau gezeichneten wurden in der JFET-Adaption verändert.
In einer eigenen Anpassung (wörtlich: „подгонка под себя“ – Anpassung an / unter sich (selbst)) wurde der Anteil der tiefen Frequenzen erhöht, indem dem Koppelkondensator nach der ersten Stufe ein Widerstand 1,2 MΩ parallelgeschaltet wurde; die Kombination 1,5 nF / 220 kΩ vor der dritten Stufe wurde entfernt. Die Größe der Kondensatoren in der (ausgangsseitigen) Klangregelung wurde von 47 nF auf 22 nF reduziert.
Anmerkungen Übersetzer: In der weiter unten in Abb. 7 dargestellten Schaltung der JFET-Adaption zeigt sich, dass die Absenkung der Bässe nach der ersten Stufe noch weiter verändert wurde.
In Röhrenverstärkerschaltung „sieht“ der kleine Koppelkondensator von 1 nF eine Schaltung um den Gainregler mit einem Widerstand von 160 kΩ bis 160 kΩ, in der JFET-Adaption hingegen nur den Gainregler mit einem Widerstand von 100 kΩ. Die Kapazität dieses Kondensators C3 wurde so auf 2 nF erhöht und ihm wurde ein Widerstand R5 = 680 kΩ parallelgeschaltet.
Weiterhin sind in der gefundenen Röhrenverstärkerschaltung die beiden Kondensatoren 47 nF im Tonestack bereits durch Kondensatoren 22 nF ersetzt worden.
Formierung des Amplitudengangs
Werden mehrere mit FETs realisierte Röhrenstufen hintereinandergeschaltet, muss bei der Berechnung des Amplitudengangs beachtet werden, dass dieser auch durch das Verhältnis von Kathodenwiderstand und -kondensator beeinflusst wird.
Dabei gibt es zwei sinnvolle Ansätze.
Im ersten Ansatz werden „Breitband“-Stufen mit einer großen Querkapazität an der Source verwendet. In diesem Fall wird der gesamte Frequenzgang durch die Beschaltung zwischen den Stufen realisiert. Die zweite Möglichkeit besteht darin, die Werte der Kondensatoren nach denen der Source-Widerständen zu berechnen. Dabei garantiert der zweite Weg nicht die vollständige Umsetzung des gewünschten Frequenzgangs; da wir es hier mit zwei Sourcewiderständen zu tun haben. So ist es praktischer, „Breitband“-Stufen zu verwenden und den gewünschten Frequenzgang zwischen den Stufen zu bilden.
Um den Amplitudengang bei Übertragung der einzelnen Stufen der Kette von der Röhrenschaltung zur FET-Variante reproduzieren zu können, ist es notwendig die unterschiedlichen Ausgangsimpedanzen von Trioden- und JFET-Stufen zu berücksichtigen. Für die 12AX7 ist die Ausgangsimpedanz einer Röhrenstufe ungefähr 3–5 mal geringer ist als der Anodenwiderstand und liegt bei etwa 30 … 45 kΩ. Bei den FET-Stufen ist der Ausgangswiderstand gleich dem Drainwiderstand. Auch hier kann man zwei verschiedene Wege gehen. Der erste Weg – den von der 12AX7 bekannte Ausgangsimpedanz (33 kΩ) als Drainwiderstand zu übernehmen. In diesem Fall werden die Frequenzgangveränderungen zwischen den Stufen unverändert in die FET-Version übernommen. Allerdings wird bei der Begrenzung der oberen Halbwelle am Drain das Verhältnis zwischen Lastwiderstand und Koppelkondensator verändert, was zu einem anderen Klirrspektrum führt. Außerdem sollte, bei einer Betriebsspannung von 30 Volt, der Drainstrom des FET mindestens 1 mA betragen.
Die zweite Möglichkeit besteht darin, Drainwiderstände mit demselben Nennwert wie in der Röhrenschaltung zu verwenden, was zu einer Begrenzung der oberen Halbwelle ähnlich der in der Röhrenschaltung führt. Dann aber ist es notwendig, die Werte der Widerstände zwischen den Stufen an die unterschiedlichen Impedanzen von FET- und der Röhrenstufe anzupassen.
Auswahl der Verstärker der Stufen
Da die Röhre mit Spannungen in der Größenordnung von 300 V und die FET-Schaltungen mit Spannungen von 30 V betrieben werden, sollte die Gesamtverstärkung der FET-Schaltung 10-mal kleiner sein, um denselben Grad der Begrenzung / Verzerrung zu erreichen. Angesichts der Tatsache, dass die Röhrenvorstufen in der 1. Stufe ohne Begrenzung arbeitet, und die zweite bei einem Signal am Eingang des Vorverstärker von über 50 mV zu begrenzen beginnt, ist es für die FET-Schaltungen ratsam, wenn die erste Stufe mit einer Verstärkung von 10, und die folgenden mit einer Verstärkung von 20 arbeiten, so dass sich am Ausgang etwa die gleiche Verzerrung ergibt wie in den beiden herkömmlichen Röhrenstufen.
Weil dabei die Eingangsstufe ohne Begrenzung arbeitet, kann sie in Sourceschaltung mit einem (frei wählbaren) Lastwiderstand und ohne Begrenzung durch eine Germaniumdiode realisiert werden, wobei ein FET mit einer Abschnürspannung von etwa 2 … 2,5 Volt verwendet wird. Die maximal mögliche Verstärkung der „Pseudotriode“-FET-Stufe kann etwa aus dem Verhältnis von der Versorgungsspannung und der Abschnürspannung der verwendeten FETs abgeschätzt werden:
\( \begin{equation} K_{\textrm{U,max}} \approx \cfrac{U_П}{U_{\textrm{CO}}} \tag{20}\end{equation} \)
Für eine Verzerrung am Ausgang gleich der bei den Röhrenschaltungen müssen die dritte und vierte Stufe die gleiche Verstärkung haben. Bei einer Versorgungsspannung von 30 V ist nur möglich, wenn FETs mit einer Abschnürspannung von 0,4 … 0,5 Volt verwendet werden. Von inländischen FETs hat beispielsweise der КПС104A (KPS104A – ein Doppel-FET) diese Abschnürspannung. Ein Doppel-FET hat noch ein weiteres „Plus“: die Möglichkeit, dass die Messung nur eines FET zur weiteren Berechnung zweier Stufen genügt. Aber möglich ist auch die Verwendung von diskreten FETs.
Schaltung des Highgain-Preamps (Lead-Kanal)

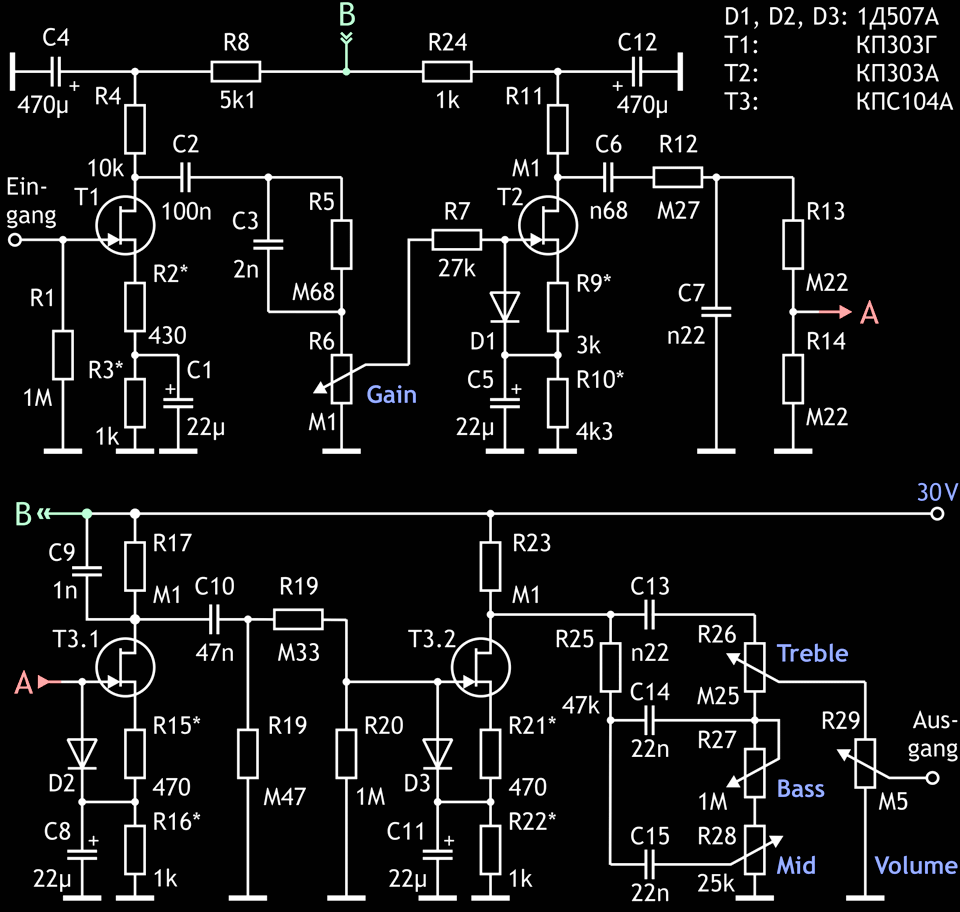
Abb. 7: Schaltung des Highgain-JFET-Preamps (Lead-Kanal). (Die oben im Originalartikel ausgewiesene Quellseite von Schaltplan und Zeichnung ist nicht mehr erreichbar – der Schaltplan wurde für diese Seite nachgezeichnet.)
-
Die Restwelligkeit der Spannungsversorgung sollte weniger als 1 mV betragen.
-
Die Widerstandspaare R2/R3, R9/R10, R15/R16 und R21 / R22 sind für konkrete Exemplare der FETs berechnet. Um die Berechnungen zu erleichtern, können Sie die beigefügte EXCEL-Datei nutzen.
-
Die Schaltung ist nicht endgültig und wird überarbeitet. Hier wird sie als Beispiel für die „Übersetzung“ einer Röhrenschaltung in eine JFET-Schaltung vorgestellt
Der Wert des Widerstand R12 wurde auf 270 kΩ reduziert und damit die Unterschiede in den Ausgangswiderstände der zweiten Stufen der Trioden- und der FET-Schaltung ausgeglichen, um den Amplitudengang (von der Röhrenschaltung zur FET-Schaltung) zu übernehmen. Der Drainwiderstand der dritten Stufe wurde auf 100 kΩ reduziert. Dabei blieb der Wert von C9 wie in der ursprünglichen Röhrenschaltung gleich 1 nF. Die letzte FET-Stufe besitzt eine Ausgangsimpedanz von 100 kΩ (35 kΩ im ursprünglichen Gerät) und unterscheidet sich so ein einigen Nuancen. Erstens hat die FET-Schaltung eine stärkere Wiedergabe der niedrigen Frequenzen von etwa 1–2 dB. Zweitens steuert die Stufe ein Tonestack mit geringerer Impedanz an, so dass die Verstärkung der Stufe ca. 6 dB kleiner als beim Original ist. Besteht der Wunsch, diese 6 dB auszugleichen, so kann R21 reduziert werden (bei gleichzeitiger Erhöhung von R22).
Der originale Röhrenverstärker und die FET-Version klingen ein wenig unterschiedlich, und das ist noch hörbar. Der Autor hat nicht versucht, absolute Identität zu erreichen – die verwendeten Widerstände haben eine Toleranz von 10 % und Kondensatoren von 20 %. Außerdem tragen die unterschiedlichen Ausgangs-Strom-Spannungs-Kennlinien von Trioden und FETs zum unterschiedlichen Klang bei. Sie können Ihre eigenen Schlüsse über die „Ähnlichkeit“ des Klanges ziehen, indem Sie sich das verlinkte Soundbeispiel anhören. Es enthält zwei identischen Aufnahmen, gespielt auf dem gleichen Instrument, in der gleichen relativen Verstärkung, mit gleich eingestellten Klangreglern und über die gleiche Box gespielt (der gesampelte Sound, 331 KB)
Fazit
Es ist wohl kaum zu erwarten, dass vergleichbare Studien nur durch den Autor des Artikels durchgeführt wurden. Es sind einige Studien bekannt, in denen bereits versucht wurde, Fragen der FET-Emulation einer Triodenverzerrung durch Transistoren zu lösen. Die US-Patente Nr. 05 647 004 und Nr. 05 619 578 können hier als Beispiel dienen. (Anmerkung Übersetzer: Es handelt sich um Patente der US-amerikanischen Firma Peavey, die als Transtube-Technologie bekannt wurden.) Die Autoren der Patente sind auch zu dem Schluss gekommen, dass die Begrenzung der positiven Halbwelle am Eingang und die Senkung der Verstärkung der Röhrenstufe durch Einfügung eines zusätzlichen Widerstands im Sourcezweig möglich sind. Aber gleichzeitig ist zu beachten, dass das Verfahren zum Begrenzen des Eingangssignals, wie im genannten Patent vorgeschlagen, keine Stabilität der Höhe der Begrenzung am Eingang gegenüber Temperaturschwankungen gewährleistet, was zu sehr signifikanten Änderungen in der Amplitude des Ausgangssignals und dementsprechend zu einer spürbaren unvorteilhaften Veränderung des Spektrums führen kann. In unserem Fall wird das eingangsseitige Cliping-Level durch die Summe der „stabilen“ Gate-Source-Spannung des FETs und des Spannungsabfalls über dem pn-Übergang der Germaniumdiode bestimmt, sodass sich die Abhängigkeit des Cliping-Levels von Temperaturschwankungen fast um Größenordnungen verringert. Darüber hinaus ist das Prinzip, das Cliping-Level aus der Gate-Source-Spannung und einer Diode mit einem niedrigen Spannungsabfall abzuleiten, stärker in Übereinstimmung mit den Prozessen, wie sie bei der einfachen Begrenzung der positiven Halbwelle mit an einer Vakuumtriode „vor Ort“ und in Echtzeit ablaufen.
Abschließend möchte ich allen danken, die mich unterstützt, bei der Suche geholfen und Ideen diskutiert haben. Ein besonderer Dank geht an Sergey Lausanne für die Durchführung der Patentsuche, für die HTML-Version dieses Artikels und für die redaktionelle Unterstützung und Igor Shaev für die freundliche Bereitstellung der Möglichkeit, einen Artikel auf dieser Seite zu veröffentlichen.
Виктор Кемпф (Viktor Kempf, AMT-Electronics) im Jahre 2006.
Zu der russischsprachigen Originalveröffentlichung als PDF: http://www.sugardas.lt/~igoramps/article68/triode_jfet_emulation.pdf
