Übersetzte Fachartikel zur Pseudo-Trioden-Verzerrung von Viktor Kempf, AMT-Electronics
Warum sich „röhrenmäßig“ nicht mit „echter Röhre“ messen kann
Kapitelinhalt:[ Überspringen ]- Vorwort •
- Triodenbasierte Begrenzung •
- Begrenzung einer Common-Source-Stufe mit ohmscher Last •
- „Pseudo-Trioden“ FET-Begrenzung •
- Ein paar Worte über die Dynamik •
- Fazit
Von Viktor Kempf, AMT-Electronics (https://amtelectronics.com)
Vorwort
Wenn es um den Gitarrensound geht, stehen die Fragen der Klangformung durch Verstärkung und Begrenzung im Vordergrund. Traditionell wird davon ausgegangen, dass nur die röhrenbedingte Begrenzung in der Lage ist, dem Gitarrensignal jene spezifische Qualität zu verleihen, die von Gitarristen und Gitarrenmusikfans so verehrt wird. Ziel dieses Artikels ist es, die grundlegenden Unterschiede zwischen der triodenbasierten Begrenzung und allen anderen Begrenzungen aufzuzeigen.
Triodenbasierte Begrenzung
Zunächst einmal wollen wir uns ansehen, wie die Triodenbegrenzung funktioniert. Zur Demonstration benötigen wir eine gängige Röhre 12AX7, die durch eine Sinusspannung ±20 V Amplitude angesteuert wird.
Die obere Halbwelle wird durch auf dem Spannungsniveau UК begrenzt (UК – Spannung an der Kathode gegen „Masse“). Wenn die Gitterspannung ansteigt, fließt der Strom zwischen dem Gitter und der Kathode. Auf diese Weise kann die Triode als eine Vakuumdiode betrachtet werden, die von der Eingangsseite her zwischen Gitter und Kathode geschaltet ist (Abb. 1).


Abb. 1: Durch die Triode verursachte positive Halbwellenbegrenzung am Gitter (UK = 1,8 V).
Dieses Phänomen ist nicht meine Entdeckung, denn es ist schon seit langem bekannt. Bei einem Kathodenwiderstand von 1 … 3 kΩ, wie er für 12AX7 üblich ist, beträgt der Pegel der oberen Halbwellensignalbegrenzung etwa 2 V.
Das Anodensignal ist das invertierte und um den Spannungsverstärkungsfaktor der Stufe KU verstärkte Signal der Eingangsstufe (Abb. 2).

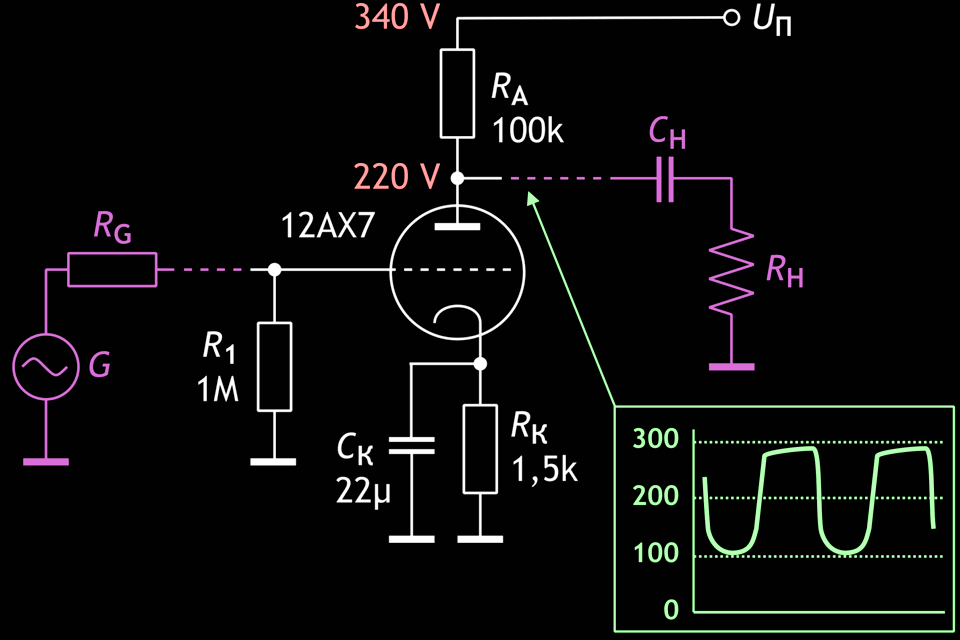
Abb. 2: Typische Verstärkerstufe mit einer Triode 12AX7.
Die Spannungsverstärkung der Stufe:
\( \begin{equation} K_{\textrm{U}} = S \cdot{} (R_{\textrm{A}}\,||\,r_{\textrm{A}}\,||\,R_{\textrm{H}})~~~\textrm{mit}~~~ r_{\textrm{A}} = \mathit{µ} × S \tag{1}\end{equation} \)
m – Verstärkung der Triodenspannung;
S – Steilheit des Arbeitspunktes;
RA – Widerstand im Anodenkreis;
rA – dynamischer Anodenwiderstand;
RН – Lastwiderstand
(Н steht vermutlich für
ноша – Last).
KU wird hauptsächlich durch den Innenwiderstand der Röhre rA bestimmt, der normalerweise 50 … 60 kΩ beträgt. In Abwesenheit einer Last beträgt die Stufenverstärkung des 12AX7 etwa 65. Betrachten wir das Ausgangssignal in Bezug auf die beiden Halbwellen. Das einzige, was die Röhre tun kann, um eine maximale Auslenkung der oberen Halbwelle zu erreichen, besteht, vollständig zu sperren. In diesem Fall wird das Maximum der positiven Halbwelle am Ausgang durch das Verhältnis zwischen RA und RН bestimmt, die einen einfachen Spannungsteiler bilden. In Abwesenheit der Last erreicht die obere Halbwelle +340 V. Bei angelegter Last (z. B. 200 kΩ) erreicht die obere Halbwelle nur +280 V. Als Ergebnis erhalten wir das in Abbildung 3 dargestellte Signal (die Steigung der Signalspitzen wird durch die Ladungsvorgänge am Koppelkondensator CН bestimmt und hängt von dessen Kapazität ab).

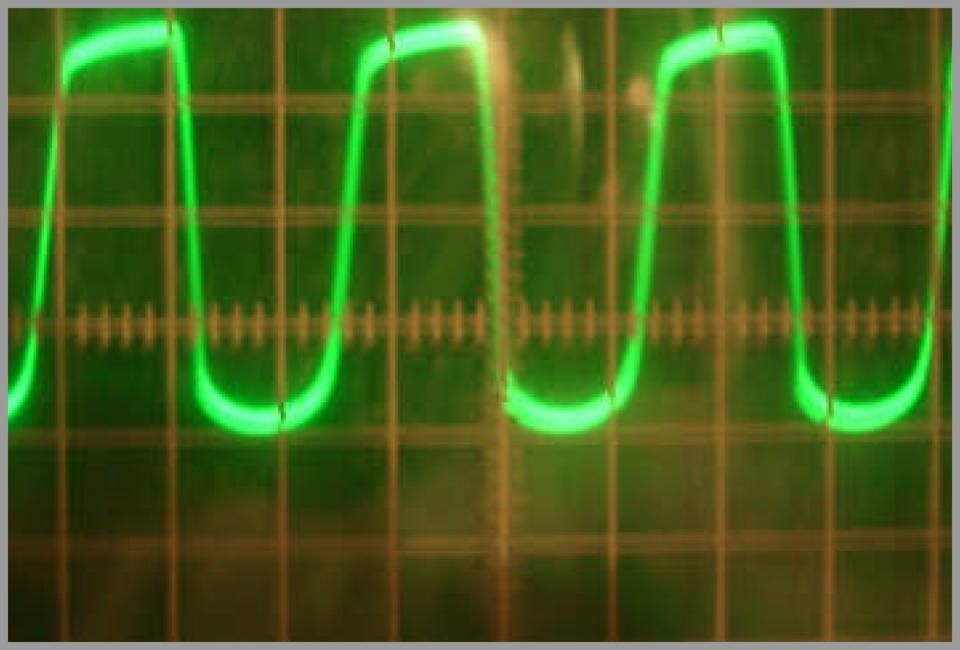
Abb. 3: Das Oszillogramm des realen Signals an der Anode (50 V / Teilung). (Oszillogramm und Foto: AMT-Electronics).
Die untere Halbwelle in dieser Abbildung ist nichts anderes als die begrenzte positive Eingangshalbwelle, die KU-fach verstärkt wurde. Da die „Eingangsdiode“ der Röhre die positive Halbwelle am Eingang um 2 V begrenzt, zeigt sich an der Anode die untere Halbwelle des Ausgangssignals mit einer charakteristischen „Dioden“-Rundung (in diesem Fall ist KU = 55, und das Signal wird bei 220 − 2 V ⋅ 55 = 110 V „gerundet“; siehe Abb. 3)
Der Ausgang der Röhrenstufe begrenzt also tatsächlich nur die obere Halbwelle.
Warum klingen die Begrenzer (Anmerkung Übersetzer: gemeint sind wohl mehr oder weniger symmetrische Halbleiter-Begrenzerschaltungen) nicht wie eine Röhre?
Nun, die Röhre begrenzt nur die positive Halbwelle – sowohl am Gitter als auch an der Anode. Da die Stufe in der Schaltung mit gemeinsamer Kathode invertiert ist, erhalten wir die Begrenzung beider Halbwellen am Ausgang der Stufe. Die Begrenzung der beiden Halbwellen erfolgt jedoch an unterschiedlichen Punkten der Verstärkungsstufe (eine Halbwelle am Gitter, die zweite an der Anode).
Diese Eigenschaft macht die Röhrenverzerrung angenehm klingend und musikalisch, da jeder Versuch, den Signalweg an einem Punkt auf beiden Halbwellen zu begrenzen, immer zu „Transistorness“ und „Schmutz“ im Klang führt.
Daher kann kein Begrenzer, ob mit Dioden in der Gegenkopplung oder im Hardclip, dem Röhrensound nahe genug kommen: symmetrisch oder asymmetrisch begrenzt er das Signal auf beiden Halbwellen. Skeptiker mögen einwenden: Zwei hintereinandergeschaltete Stufen mit Vakuumtrioden sorgen ebenfalls für eine (gitter-)strombasierte Begrenzung auf beiden Halbwellen und bilden schließlich aus einem sinusförmigen Signal eine Art beidseitig abgerundete Kurve (wörtlich: „Mäander“). Aber die Signalbegrenzung erst über die eine und dann über die andere Halbwelle ist nicht dasselbe wie die gleichzeitige Begrenzung beider Halbwellen. Das echte Gitarrensignal ist nicht sinusförmig; eher vielgestaltig (wörtlich: es gibt viele davon). Deshalb ist das Spektrum der Intermodulationsverzerrungen, die durch die Triodenkaskade geformt werden, so wohlklingend – die unteren / tieferen der neu entstehenden Töne sind mit dem Hauptton konsonant. Im Falle der gleichzeitigen zweiseitigen Begrenzung an Operationsverstärkern oder den Schaltungen mit diskreten Transistoren enthält das Spektrum der Intermodulationsverzerrungen eine große Anzahl von nicht-musikalischen kombinierten Komponenten, die nicht mit dem Hauptton übereinstimmen, was als „Schmutz“ im Klang wahrgenommen wird. Daher ist es lächerlich, zu versuchen, den Klang von Begrenzungsstufen mit Operationsverstärkern mit Dioden in negativer Rückkopplung durch die Verwendung einer unterschiedlichen Anzahl von Dioden für die obere und untere Halbwelle „röhrenartig edel“ zu machen. Dadurch werden bei der Verarbeitung von Einzeltönen wahrscheinlich ein paar gleichmäßige Obertöne erzeugt, aber wenn ein zweiter Ton im Signal auftaucht, wird der Klang sofort verunreinigt.
Um das oben Gesagte zu beweisen, wollen wir die Ausgangssignale der Transistoren (Anmerkung Übersetzer: „signals ranges at the output of the transistor“ – sind hier nicht die Ausgangssignale von Röhren gemeint?) in zwei Fällen veranschaulichen:
Eine Standardtriodenstufe und eine Standardstufe mit einer zusätzlichen Vakuumdiode zwischen Gitter und Masse (zur beidseitigen Begrenzung am Gitter).
Die Eingänge der Stufen werden mit einem Zweiton-Signal von 200 Hz (10 V) und 300 Hz (10 V) gespeist.
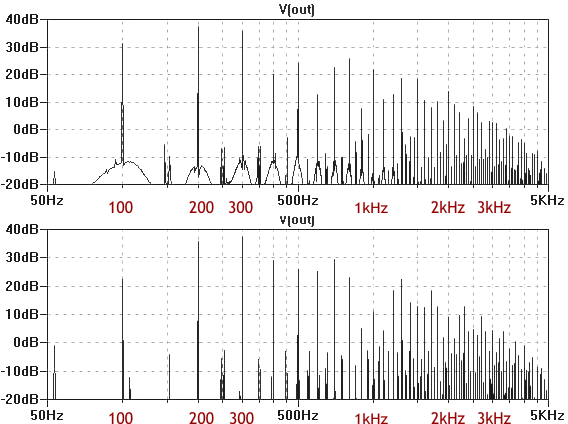
Doppelspektrum 1: Ausgangssignalspektren einer Standardtriodenstufe (oben) und einer Standardstufe mit zusätzlicher Vakuumdiode zwischen Gitter und Masse (unten). (Anmerkung Übersetzer: Abbildung generiert aus Oszilloskopen-Foto im Originalartikel)
Zunächst einmal ist der hohe Pegel der Differenzfrequenz 100 Hz ziemlich auffällig (das ist es – die Leistung und Dichte der Röhre). Der Pegel ist 10 dB höher als der der Stufe mit Zwei-Wege-Begrenzung am Gitter (unteres Spektrogramm).
Zweitens ist die Struktur der dominanten Töne im oberen Spektrogramm viel strukturierter: Mit Ausnahme der Signale bei 800 Hz und 1,3 kHz sind alle dominanten Töne die Summe der mit einer ganzen Zahl multiplizierten Anfangstöne.
Unsere Ohren „lieben“ konsonantische Töne, daher ist es nicht verwunderlich, dass ihnen das Spektrum in der unteren Abbildung viel unmusikalischer und „schmutziger“ vorkommt, weil seine Struktur viel schlechter ist.
Es ist auch anzumerken, dass bei der Begrenzung einer einzelnen Sinuskurve die Unterschiede in den Spektren der oben genannten Stufen minimal sind.
Noch schlimmer ist die Situation bei Begrenzern, die auf Operationsverstärkern basieren.
Unten sehen Sie die Spektrogramme der Signale, die am Ausgang einer invertierenden Operationsverstärkerstufe mit Begrenzung an der Betriebsspannung (wörtlich: „feed limitation“) und einer Stufe in Kathodenschaltung aufgezeichnet wurden. Am Eingang wurden zwei Töne – 100 Hz und 200 Hz – eingespeist (die Amplitude des Eingangssignals wurde im Falle des Operationsverstärkers proportional verringert, um eine identische Begrenzungsschwelle der Stufe sicherzustellen).
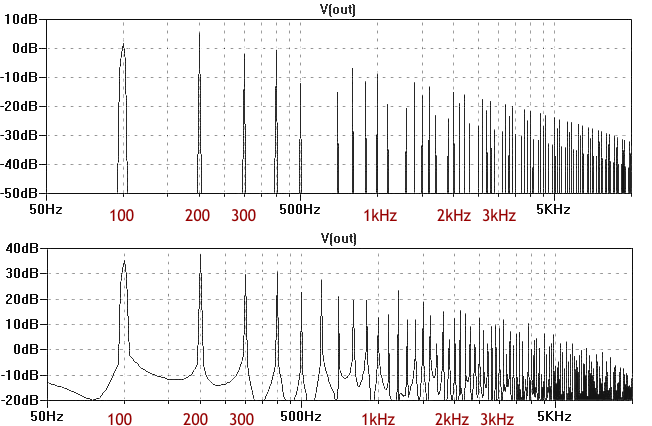
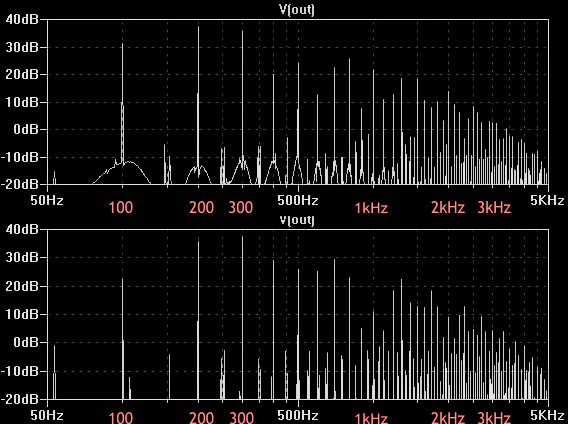
Doppelspektrum 2: Ausgangssignalspektren eines übersteuerten Operationsverstärkers (oben) und einer Stufe in Kathodenschaltung (unten). (Anmerkung Übersetzer: Abbildung generiert aus Oszilloskopen-Foto im Originalartikel)
Ganz offensichtlich ist die Dominanz der gesamten tonalen Obertöne von 100 Hz und 200 Hz: 600 Hz, 1,2 kHz, 1,8 kHz usw. in der unteren Abbildung (Begrenzer mit gemeinsamer Kathode), während sie im Spektrum des Begrenzers mit Operationsverstärker in der oberen Abbildung praktisch völlig fehlen. Trotz der hohen Ordnung der Spektralkomponenten in der oberen Abbildung sind sie jedoch in Bezug auf den Gesamtton nicht konsonant und werden von uns als Rauschen oder „Schmutz“ wahrgenommen, der in die Eingangstöne gemischt ist.
Bei den von einer Gitarre erzeugten Ausgangstönen werden alle oben genannten Phänomene am intensivsten im Frequenzbereich von 400 Hz bis 3 kHz wahrgenommen. Im Falle von Röhrenbegrenzern genießen wir daher die Schönheit des Spektrums in diesem Bereich. Bei zweiseitigen Begrenzern neigen die Entwickler dazu, zumindest einen gewissen Wohlklang zu erzeugen, indem sie die informativsten „Mitten“ vollständig herausschneiden und die tiefen Frequenzen anheben. Es bleibt ihnen auch nichts anderes übrig (wörtlich: Es gibt jedoch keinen anderen Weg). Sie können deutlich sehen, dass der Pegel des Differenztons im Falle einer zweiseitigen Begrenzung niedriger ist.
Was sonst sollten sie mit einem Spektrum tun, das von Beginn an nicht mit dem resultierenden Ton übereinstimmt?
Leider wird die zweiseitige Begrenzung, abgesehen von der Triodenbegrenzung, von fast allen Begrenzungsstufen vorgenommen, unabhängig davon, ob sie auf Operationsverstärkern oder auf Schaltungen mit diskreten Transistoren basieren. Das Verständnis dieser Tatsache ist der Schlüssel zur Erzielung eines „richtigen“ Röhrenklangs aus transistorbasierten Geräten.
Begrenzung einer Common-Source-Stufe mit ohmscher Last
Von allen Transistortypen kommen die FETs mit ihren (den Pentodenkennlinien sehr ähnlichen) Kennlinien und mit einem hohen Widerstand im Bereich des Gates den Röhren am nächsten.
Der JFET (n-Kanal-Bauelement auf der Basis des p-n-Übergangs) besteht eingangsseitig aus einer Diode, die das Eingangssignal von oben begrenzt. Der Begrenzungspegel ist gleich Up-n + US, mit
Up-n – Spannungsabfall am Silizium-pn-Übergang;
US – Sourcespannung.

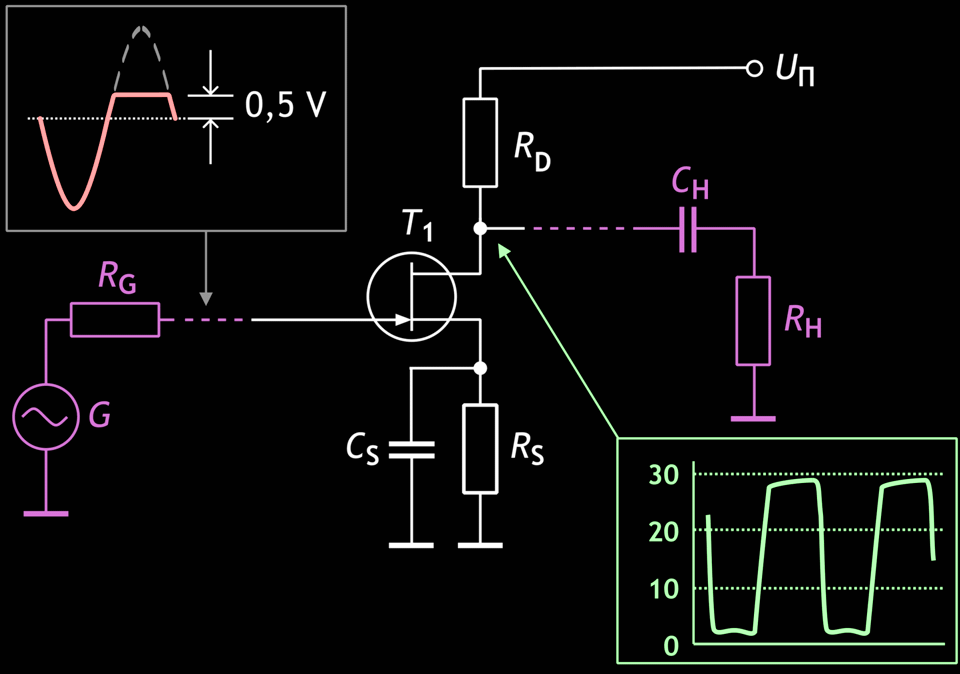
Abb. 4: Common-Source-Stufe, die am Ausgang und am Eingang begrenzt ist.
Das Problem des FET in der Schaltung mit Common-Source-Stufe und ohmscher Last besteht darin, dass er es „schafft“, die untere Halbwelle des Ausgangssignals in gleicher Weise zu begrenzen wie die obere. Dies geschieht übrigens schon, „bevor“ (d. h. schon bei kleineren positiven Eingangsspannungen) das Signal am Eingang begrenzt wird (Abb. 4). Wenn diese Begrenzung am Eingang einsetzt, ist der JFET bereits vollständig durchlässig, und der gesamte Eingangsstrom mischt sich mit dem Strom durch den FET-Kanal. Dieser Strom verändert leicht das Ausgangssignal und bildet auf der unteren Halbwelle den so genannten „Rückwärtsbiss“ (Anmerkung Übersetzer: eine nach oben gerichtete Einstülpung der unteren Kante des ausgangsseitigen Rechtecksignals). Der Effekt kann etwas abgeschwächt werden, indem man einen großen Widerstand (0,4 … 1 MΩ) vor das Gate schaltet. Aber diese Methode zur Verringerung des „Bisses“ beseitigt nicht die ausgangsseitige Signalbegrenzung der unteren Halbwelle. Die FETs selbst können also nicht wie eine übersteuerte Triode klingen. Dies gilt auch für alle Common-Source-Stufen, einschließlich der μ-Stufen. Es sollte gesagt werden, dass Vakuumpentoden aus dem gleichen Grund nicht in Gitarrenvorverstärkern verwendet wurden: da sie eine große Verstärkung haben, verhalten sie sich wie eine Common-Source-Stufe und begrenzen das Signal am Ausgang der Stufe über beide Halbwellen, was im Allgemeinen ihre mangelnde Eignung beim Bau von Gitarrenvorverstärkern vorbestimmt.
„Pseudo-Trioden“ FET-Begrenzung
Jetzt wissen wir, wie das Bild der Signalbegrenzung durch eine Triodenstufe aussieht, und wir wissen auch, warum die FET-basierte Common-Source-Stufe nicht die richtige Begrenzung bietet. Das Hauptproblem ist, dass der relative Pegel der Eingangsbegrenzung der FET-Stufe viel höher ist (als bei der Röhre). Lassen Sie uns versuchen, dieses Problem zu lösen.
-
Wenn man sich das Verhältnis zwischen der Betriebsspannung einer Triode und dem Begrenzereinsatz am Eingang (200 … 400 V / 1 … 3 V) vor Augen hält, sollte der FET mit der höchstmöglichen Betriebsspannung betrieben werden. Außerdem müssen wir Bauelemente mit niedriger Abschnürspannung verwenden.
-
Zweitens sollten wir zur Verringerung des eingangsseitigen Begrenzereinsatzes eine Siliziumdiode oder ein Schottky-Diode (Anmerkung Übersetzer: hier wörtlich „silicon diode or Schottky diode“; später aber sinnvollerweise Germanium- oder Schottkydiode) verwenden, die parallel zum FET-Übergang geschaltet wird.
-
Drittens sollten wir für die Stufe eine Spannungsverstärkung vorsehen, mit der die eingangsseitig begrenzte positive Halbwelle, multipliziert mit dem Spannungsverstärkungsfaktor KU der Stufe, nicht zu einer ausgangsseitigen Begrenzung der unteren Halbwelle führt. Dies lässt sich am einfachsten durch die Einführung eines zusätzlichen Widerstands in der Source erreichen.
Die folgende Abbildung zeigt die FET-basierte Stufe, die alle diese Bedingungen erfüllt:

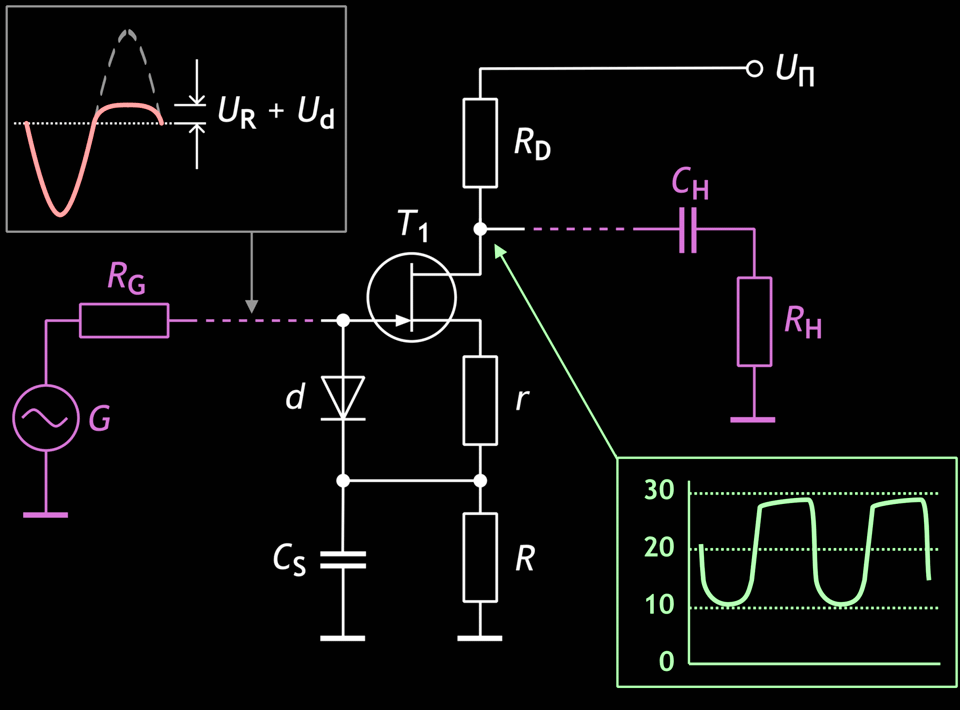
Abb. 5: Common-Source-Stufe mit „Trioden“-Begrenzung.
Die Besonderheit der Stufe liegt in der Verwendung einer Diode mit geringem Spannungsabfall in Durchlassrichtung (Germanium oder Schottky).
Ein paar Worte über die Dynamik
Kapitelinhalt:[ Überspringen ]- Formierung des Amplitudengangs •
- Signalpegel •
- Dichte des Spektrums •
- Tastverhältnis der Begrenzung •
Es gibt eine weitere interessante Eigenschaft der Transistoren (Anmerkung Übersetzer: „There is another interesting feature of the transistors“ – sind hier nicht eher die interessanten Eigenschaften von Röhren gemeint?), die von Gitarristen sehr geschätzt wird. Das ist die so genannte „Röhrendynamik“. Aus der Sicht eines Gitarristen ist die Dynamik eine sehr spürbare Abhängigkeit des Signals vom Ausgang des Verzerrers von der physikalischen Einwirkung auf die Saiten. Natürlich bietet sie zusätzliche Möglichkeiten für die emotionale Färbung des Spiels.
Betrachten wir die „Dynamik“ einmal aus der Sicht eines Ingenieurs.
Aus der Sicht eines Ingenieurs ist die Röhrendynamik die Abhängigkeit vom Pegel des Eingangssignals in Bezug auf die drei Parameter:
-
Signalpegel
-
Dichte des Spektrums
-
Tastverhältnis der Begrenzung.
Signalpegel
Der Pegel des begrenzten Signals am Ausgang der Röhrenstufe ist aus zwei Gründen vom Pegel des Eingangssignals abhängig: Zum einen steigt die untere Halbwelle des Ausgangssignals an, da die Vakuumdiode am Eingang eine sehr weiche dynamische (Widerstands-)abhängigkeit von der angelegten Spannung aufweist. Darüber hinaus ist aber auch ein Anstieg des „oberen“ Teils des Ausgangssignals zu beobachten, der durch die Verschiebung des „unteren Arbeitspunkts“ unter dem Einfluss der großen Eingangsamplitude verursacht wird. Die Erhöhung des (mittleren) Kathodenpotentials führt zu einer Verschiebung des unteren Arbeitspunktes sowie zu einer zusätzlichen Erhöhung der oberen Halbwelle. Dies geschieht aufgrund der Tatsache, dass der Gitterstrom mit dem Anodenstrom verschmilzt. Da beide durch den Kathodenwiderstand fließen, erhöht der Spannungsabfall über ihm.
(Anmerkung: Die Wirkung dieser Komponente
wird oft durch einen Kondensator im Kathodenkreis des
Transistors blockiert, daher ist es offensichtlich, dass
Kaskaden mit und ohne Kathodenkondensator
(wörtlich: cathode
shunt) nicht nur einen unterschiedlichen dynamischen
Ausgangswiderstand haben, sondern auch eine
unterschiedliche Dynamik – Stufen ohne
Kathodenkondensator haben eine etwas deutlicher
ausgeprägte Dynamik).
Dichte des Spektrums
Bei Verzerrungen mit wenig Gain sorgt die ausgeprägte Abhängigkeit von Ausgangspegel, spektraler Dichte und verstärktem Eingangssignal für das von Gitarristen so geschätzte Spielgefühl. Schließlich spüren sie regelrecht, wie sie den Begrenzungsprozess kontrollieren.
Natürlich kann auch ein Operationsverstärker mit Dioden im Gegenkopplungskreis eine gewisse „Dynamik“ erzeugen, aber in diesem Fall sollte man Siliziumdioden verwenden, die eine ziemlich abrupte Änderung des dynamischen Widerstands im Bereich von 0,4 … 0,6 V aufweisen; diese Art von Dynamik zeigt sich in einem sehr engen Bereich, und es ist – gelinde gesagt – nicht einfach, sie zu nutzen. Die Option, mit Operationsverstärkern Verzerrungen an der Versorgungsspannung zu erzeugen, ist völlig frei von jeglicher Art von Amplitudendynamik: In diesem Moment manifestiert sich die gesamte Dynamik nur in der Beschränkung des Verzerrungsspektrums in Abhängigkeit vom Eingangssignalpegel.
Tastverhältnis der Begrenzung
Und schließlich das Tastverhältnis. Das Tastverhältnis ist im Wesentlichen das Verhältnis zwischen der „Breite“ der oberen und unteren Halbwellen am Ausgang des Verzerrers. Bei schwachen Signalen ist das Tastverhältnis nahe dem einer gleichmäßigen Schwingung (wörtlich: eines Mäanders), aber mit zunehmendem Signal erhält das Spektrum mehr gleichmäßige niederfrequente Obertöne, die die Ohren gut hören können. Die Röhrenbegrenzer haben aufgrund ihres mehrstufigen Aufbaus eine stärker ausgeprägte Abhängigkeit des Tastverhältnisses vom Pegel des Eingangssignals, und bei den High-Gain-Verzerrern tritt diese Komponente manchmal in den Vordergrund. Schaltungen auf Basis von Operationsverstärkern weisen eine solche Abhängigkeit kaum auf, und selbst die Tricks in Form einer ungleichen Anzahl von Dioden im Rückkopplungskreis des Operationsverstärkers führen nicht zu einem röhrenähnlichen Klang des Verzerrers, da die Änderungen des Tastverhältnisses unbedeutend sind.
Die vorgeschlagene Pseudo-Triodenstufe auf FET-Basis mit einer Stromverteilung, die der einer echten Vakuumtriode ähnelt, verhält sich auch in Bezug auf die Dynamik ähnlich – wir haben den gleichen gleichmäßigen Anstieg des unteren Teils des Ausgangssignals (diese Gleichmäßigkeit ist auf die statische Kennlinie des Germanium-Übergangs zurückzuführen, der der statische Kennlinie einer Vakuumdiode nahe kommt), wobei sich der Arbeitspunkt mit steigendem Eingangssignal nach oben verschiebt, was uns genau das gleiche Verhalten der Stufe wie das einer herkömmlichen Triode liefert. Wenn Sie also mit einem Pseudo-Triode-Gerät spielen, erleben Sie in Bezug auf die Dynamik dasselbe Gefühl wie bei einem Röhrenvorverstärker.
Fazit
Es ist schwierig, etwas zu schaffen, das absolut perfekt ist. Deshalb ist die vorgeschlagene Stufe auch kein vollständiger Ersatz für die Röhre. Ich möchte daran erinnern, dass bei der Entwicklung der Stufe der Schwerpunkt genau auf dem Begrenzungsverhalten lag. Das Verhalten der Stufe im „linearen“ Bereich blieb fast völlig unbeachtet. Aber auch hier gibt es eine sehr interessante Beobachtung – die gegenseitige Kompensation der Nichtlinearitäten der zusätzlichen Diode und des Feldeffekttransistors (der, gegenüber der 3 / 2 -Eingangskennlinie der Röhren, eine quadratische Eingangskennlinie hat), führt bei gründlichen Berechnungen letztlich zu einer teilweisen Linearisierung im „linearen Bereich“ des JFETs und bringt das Verzerrungsspektrum sehr nahe an das der Triode, und das auch ohne Begrenzungen.
Wir lieben den röhrenbasierten Sound und den Klang von Triodenverzerrungen. Eine Röhre ist ein bekannter und ausgetretener Weg zur Wahrheit, aber es ist nicht der einzige Weg. Wir haben nie geglaubt, dass die oben beschriebenen Forschungen ausschließlich vom Autor des Artikels durchgeführt wurden. Uns sind einige Arbeiten bekannt, die sich mit der Emulation der Triodenbegrenzung auf FET-Basis beschäftigen. Zum Beispiel die folgenden Patente: US-Patent 5,647,004 und US-Patent 5,619,578. (Anmerkung Übersetzer: Es handelt sich um Patente der US-amerikanischen Firma Peavey, die als Transtube-Technologie bekannt wurden.) Die Autoren der Patente hielten es ebenfalls für notwendig, die positive Halbwelle an der Eingangs- und Begrenzungsverstärkungsstufe durch die Einführung eines zusätzlichen Widerstands in den Source zu begrenzen. Gleichzeitig ist jedoch anzumerken, dass der Grad der in diesen Patenten umgesetzten Eingangsbegrenzung:
-
wesentlich von der Temperatur abhängig ist, was zu erheblichen Schwankungen der Ausgangssignalamplitude führt (und im Falle der Begrenzung des Ausgangssignals nach unten – zu einer erheblichen Verschlechterung des Spektrums). In unserer Lösung ist der Pegel der Eingangsbegrenzung die Summe der „konstanten“ FET-Gate-Source-Spannung und des Spannungsabfalls über dem Germanium-Übergang, was den Begrenzungspegel viel weniger empfindlich gegenüber Temperaturänderungen macht.
-
Wie bereits in den Patenten erwähnt, fließt im Falle einer Eingangsüberlastung in dieser Stufe kein dem Gitter-Kathoden-Strom vergleichbarer Strom, wodurch die Arbeitspunktverschiebung in Abhängigkeit vom Pegel des Signals am Eingang der Stufe nicht zur Wirkung kommt. Dementsprechend fehlt in diesem Fall die erforderliche „röhrenartige“ Dynamik.
Die (von uns) vorgeschlagene Schaltung einer Verstärkerstufe unterscheidet sich davon dahingehend, dass die Ableitung des Begrenzungslevels aus der Gate-Source-Spannung und der Durchlassspannung der Schottky-Diode mehr mit den Vorgängen in der realen Vakuumtriode übereinstimmt als die einfache Begrenzung der positiven Halbwelle durch eine „geerdete“ Diode.
Die (von uns) vorgeschlagene Schaltung einer Verstärkerstufe bildete die Grundlage für die derzeit von AMT hergestellte LA-Serie. Aber die Zeit schreitet voran und die Auswahl an Bauteilen wird immer größer, so dass wir weiterhin aktiv das „Phänomen“ des Röhrenklangs studieren und bessere Wege der Klangemulation entwickeln. Wir hoffen, dass AMT seinen Fans in naher Zukunft weitere innovative Entwicklungen anbieten kann.
© AMT-Electronics
(https://amtelectronics.com)
© Viktor Kempf, AMT-Electronics
Der englischsprachige Originalartikel wurde mit „Datumsstempel“ 28. 3. 2016 von der Internetseite von AMT-Electronics heruntergeladen und findet sich aktuell unter dem Link https://media.amtelectronics.com/why-tube-like-cannot-measure-up-to-tube-inside/ .
