ПРИМИТИВ – Schlager-Fuzz Paula – Teil II
Si simuliert Ge (I) – Low-Gain-Leistungstransistoren
Kapitelinhalt:[ Überspringen ]- Was war •
- Erster Ansatz – Leistungstransistoren •
- Das Ergebnis enttäuscht •
- Nochmal nachdenken •
- Ausblick
Was war
Es wurde ein erweitertes Fuzz Face mit Germaniumtransistoren geringer Verstärkung gebaut, dessen Klang überraschend gut war und das stark rauscht. Letzteres sollte (in einer neuen Schaltung) geändert werden.
Die Dimensionierung des Fuzz Face war dabei ein wenig „neben der Norm“ – der Eingangstransistor T1 arbeitete mit einer für ein Germanium-Fuzz recht hohen Kollektorspannung (etwas mehr als 1 V, also nicht ganz kurz vor der Sättigung), der Speisewiderstand für den ersten Transistor war recht hoch und der Kollektorwiderstand von T2 gering, so dass sich für T2 eine recht hohe Kollektorspannung ergab. Mit diesem Arbeitspunkt wie bei einem Treblebooster (UC2 ≈ 7 V) gefiel der Zerrklang wesentlich besser als mit einer Kollektorruhespannung in Höhe der halben Betriebsspannung.
Eine weitere spezielle Eigenschaft, die die Arbeitspunkte von T1 und T2 beeinflusst, ist der sehr hohe Reststrom von Germaniumtransistoren – beispielsweise führt bei T1 ein Reststrom von etwa 120 µA zu einem Spannungsabfall von etwa 4 Volt an dessen Kollektorwiderstand R4 (33 kΩ).
Erster Ansatz – Leistungstransistoren
Der erste Ansatz, das Rauschen einer solchen Schaltung zu verringern, ist der Ersatz der Germanium- durch Siliziumtransistoren. Aber durch welche? Abgesehen von speziellen Eigenschaften von Germaniumtransistoren beim Cut Off (die hier nicht diskutiert werden können und sollen) haben real verfügbare Siliziumtransistoren i. A. eine wesentlich größere Stromverstärkung und einen wesentlich geringeren Reststrom.
Insofern schien es für die Emulation der beschriebenen Fuzz-Schaltung durch Siliziumtransistoren sinnvoll, einen Trick zu finden, um die geringe Stromverstärkung der Germaniumtransistoren nachzubilden.
Der erste Ansatz war die Verwendung von Leistungstransistoren, bauartbedingt einen wesentlich einen geringeren Stromverstärkungsfaktor haben. Dazu war zunächst, wieder dem Bastel- und Inspirationsprinzip „Zufall & Abfall“ folgend, die Verwendung von Transistoren DK55 aus alten Energiesparlampen erwogen worden. Diese schienen jedoch nicht mehr funktionsfähig zu sein.
Im Netz war der Typ MJE13005 als Ersatz für den DK55 ausgewiesen worden – der Verkäufer bei Conrad (immer wieder ein Erlebnis) belehrte dann sich und seinen Bart, dass die in seinem Regalsystem vorhandenen MJE13007 „auch gehen“, da mit dem gleichen Maximalstrom belastbar. Nun denn, dann eben ein MJE13007.
Als Alternative wurden noch etwas kleinere Leistungstransistoren (mit möglicherweise etwas größerem Stromverstärkungsfaktor) MJE340 beschafft und die Transistoren auf dem Breadboard mit einer Widerstandskette ausgemessen und deren ungefähre Stromverstärkungsfaktoren bestimmt.

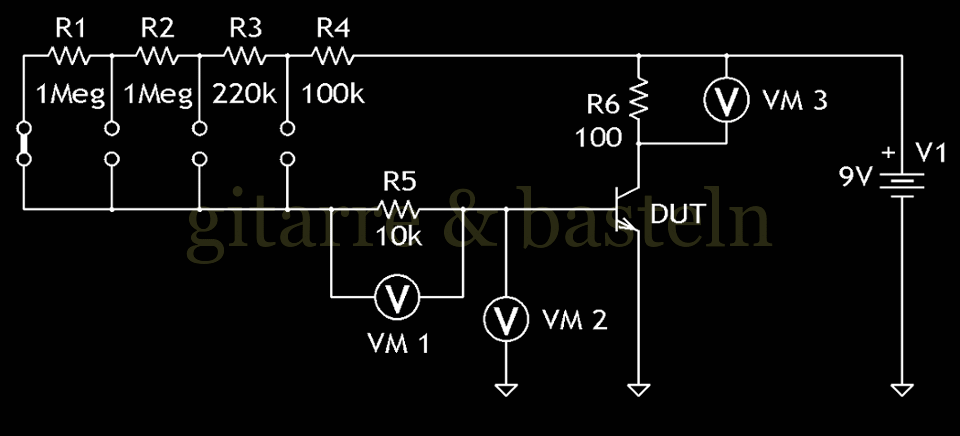
Abb. 2.1: Bestimmung der Stromverstärkungsfaktoren der Leistungstransistoren
Es wurden von jedem Typ zwei Exemplare untersucht, die folgende Tabelle 2.1 zeigt die Messwerte:
| Transistor | UB [V] |
IB [µA] |
IC [mA] |
ΔIC / ΔIB |
|---|---|---|---|---|
| MJE340 (1) | 0,56 | 3,7 | 0,14 | — |
| 0,58 | 6,3 | 0,28 | ≈ 53 | |
| 0,62 | 25 | 1,48 | ≈ 62 | |
| 0,65 | 76 | 4,67 | ≈ 62 | |
| MJE340 (2) | 0,54 | 3,6 | 0,18 | — |
| 0,55 | 6,4 | 0,33 | ≈ 55 | |
| 0,59 | 26 | 1,56 | ≈ 64 | |
| 0,62 | 77 | 5,03 | ≈ 67 | |
| MJE13007 (1) | 0,49 | 3,8 | 0,07 | — |
| 0,51 | 6,6 | 0,13 | ≈ 20 | |
| 0,55 | 26 | 0,54 | ≈ 21 | |
| 0,58 | 78 | 1,67 | ≈ 22 | |
| MJE13007 (2) | 0,49 | 3,6 | 0,07 | — |
| 0,51 | 6,4 | 0,13 | ≈ 21 | |
| 0,55 | 26 | 0,56 | ≈ 22 | |
| 0,58 | 77 | 1,73 | ≈ 23 |
Zuerst zu den Stromverstärkungsfaktoren: Die beiden Typen von Leistungstransistoren haben also tatsächlich relativ geringe Stromverstärkungsfaktoren, (55 bis 60 und etwas mehr als 20), die der beiden im Germanium-Fuzz verwendeten Transistoren lagen bei 35 (32 und 36). Das Produkt der Stromverstärkungsfaktoren beider Transistoren aus dem Germanium-Fuzz ist so etwa gleich dem Produkt der Stromverstärkungsfaktoren der beiden Transistoren MJE340 MJE13007.
Insofern lag die Überlegung nahe, den nächsten Versuch mit einem MJE340 für T1 und einem MJE13007 für T2 aufzubauen und der unterschiedlichen Stromverstärkungsfaktoren wegen den Kollektorwiderstand von T1 anzupassen. Will sagen, wenn der Stromverstärkungsfaktor von T1 im „Siliziumfuzz“ etwa eineinhalbmal so groß ist wie der im „Germanium-Fuzz“, so muss der Kollektorwiderstand für eine gleiche Verstärkung dieser Stufe auch eineinhalbmal so klein sein. Der Wert für den Kollektorwiderstand von T1, R4, wurde also auf 33 kΩ auf 22 kΩ verkleinert.
Die zweite Frage betrifft die Simulation der Restströme, insbesondere des Reststromes von T1. Um die Wirkung Wirkung dieses Reststroms zu verstehen, soll noch einmal die Schaltung mit den Germaniumtransistoren betrachtet werden.
Der Reststrom von T2 ist dabei weniger wichtig, die Ausgangsstufe ist niederohmig (maximal einige kΩ) und ein Reststrom von bis zu 150 µA führt hier bestenfalls zu einer Änderung der Kollektorspannung von etwa einem Volt, die auch noch über die vorgesehene Einstellung dieser Spannung kompensiert wird.
Hat T1 jedoch einen Reststrom gleicher Größe, so liegt am Kollektorwiderstand R4 des unbeschalteten T1 eine Spannung von etwa 4 Volt an. Das bedeutet weiterhin, dass auch bei negativer Eingangsspannung des Fuzz' T1 nicht vollständig sperrt, so dass ein Teil des Stroms durch R4 nicht in die Basis von T2 fließen kann, sondern als Reststrom von T1 aufgenommen wird. Der Reststrom führt T1 also zu einer verringerten Aussteuerung von T2. Er könnte dafür sorgen, dass T2 nicht vollständig in die Sättigung kommt und somit für die untere Halbwelle an seinem Kollektor weniger hart klippt und tendenziell lediglich den Cut Off von T1 weiterverstärkt.
Die Simulation dieses Reststroms erfolgte über einen Stromspiegel. Dazu wird ein zweiter Transistor vom Typ MJE340 als T3 in die Schaltung eingefügt. Er hat einen (zunächst) einstellbaren Kollektorwiderstand R13, sein Kollektor ist über zwei gleiche Widerstände R14 und R15 jeweils mit der Basis von T1 und T3 verbunden.
Schließlich wurde vor den Stromspiegel und die Basis von T1 eine Schottky-Diode geschaltet. Diese soll verhindern, dass der über den Stromspiegel simulierte „Reststrom“ von T1 bei starker negativer Aussteuerung „rückwärts“ aus dem Eingang des Fuzz herausfließt. Im Ruhezustand und im nicht übersteuerten Betrieb ist diese Diode leitend, da durch R1 der normale Speisestrom in die Basis von T1 fließt.
Zur Übersicht hier in Abbildung 2.2 zunächst die Schaltung des Versuchsaufbaus. Die Klangregelschaltung wurde aus dem Germanium-Fuzz übernommen und lediglich im Faktor von etwa zwei hochohmiger ausgeführt – es stand einfach kein logarithmisches Poti 10 kΩ zur Verfügung. Da es hinter der Klangregelschaltung mit dem Volumenpoti ohnehin hochohmig weitergeht, sind hier keine Klangveränderungen zu erwarten. Zumindest für einen Versuchsaufbau sollte es reichen:

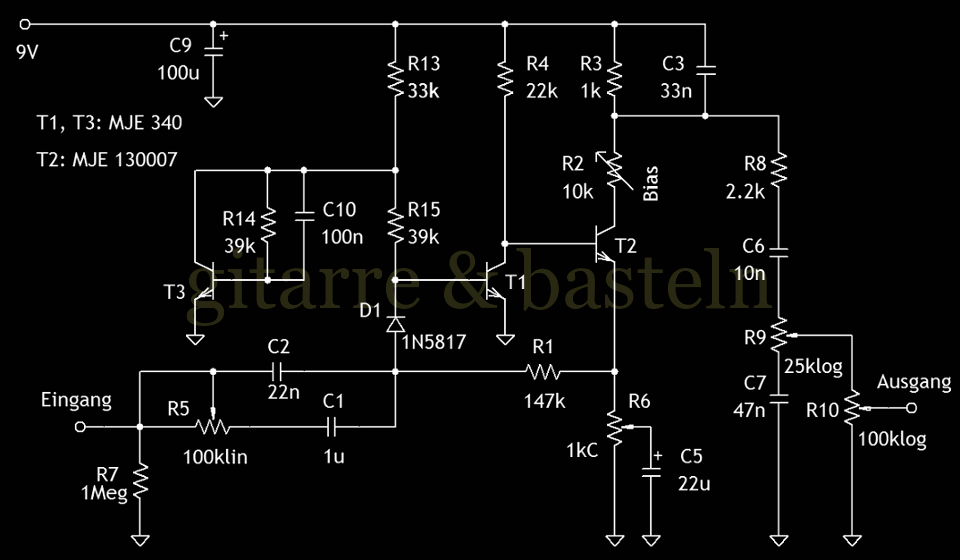
Abb. 2.2: Schaltung des Versuchsaufbaus eines Fuzz mit Leistungstransistoren.
Einstellungen
Nach dem Aufbau erfolgte die Einstellung der Arbeitspunkte für T1 und T2 – siehe auch Abbildung 2.3. Zuerst war der simulierte Reststrom von T1 über Festlegung der Größe des Kollektorwiderstands von T3 eingestellt worden – dazu (um einen zusätzlichen Zufluss an Basisstrom und Abfluss von Kollektorstrom auszuschließen) wurde T2 vom Breadboard entfernt. Mit einem Kollektorwiderstand RC3 (d. h. R13) von 33k stellte sich am Kollektor von T2 eine Spannung von 5 Volt ein. Nun konnte T2 wieder eingesetzt werden.

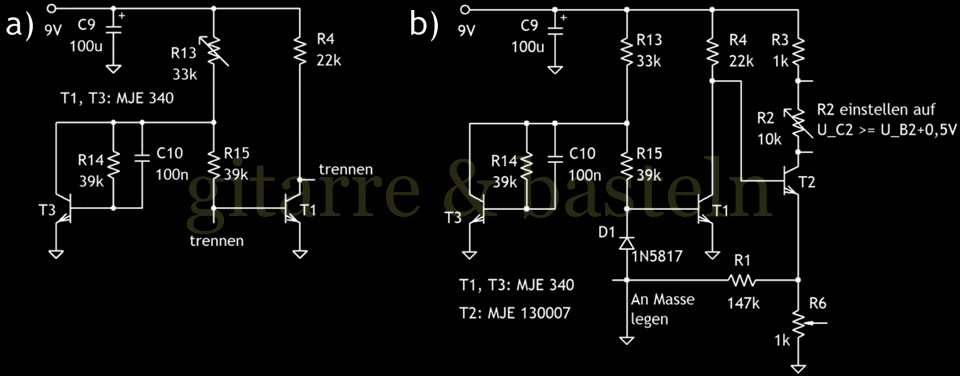
Abb. 2.3: Einstellung der Arbeitspunkte bzw. der Reststromsimulation in der Schaltung nach Abbildung 2.2 – links die Einstellung des simulierten Reststroms über R13, rechts die Einstellung der Kollektorruhespannung von T2 durch R2.
Um für T2 die größte Aussteuerung zu simulieren, wurde die Anode von D1 (Diode D1 vor der Basis von T1) mit Masse verbunden, d. h. dafür gesorgt, dass D1 sperrt und in die Basis von T1 nur noch der (simulierte) Reststrom fließt. Jetzt wurde der Kollektorwiderstand von T2 so eingestellt, das dessen Kollektorspannung etwa ein halbes Volt größer als seine Basisspannung war. Das heißt:
UC2,min ≈ 3,5 V
UB2,min ≈ 3,0 V
Nach Aufhebung des genannten Kurzschlusses stellte sich eine Kollektorspannung UC2 von etwa 6,8 V ein, die Basisspannung von T2 (und Kollektorspannung von T1) betrug etwa 1,6 V. Das entspricht in etwa, berücksichtigt man die höheren Basis-Emitter-Spannungen von Siliziumtransistoren, den Arbeitspunkteinstellungen des „Germanium-Fuzz“.
Das Ergebnis enttäuscht
Insgesamt enttäuschend: Das Gain war wesentlich geringer, nur bei maximalem Attack und starkem Anschlag mindestens der Quinte, wenn nicht noch der Oktavsaite darüber, war eine einigermaßen satte Distortion zu hören – die Verzerrung war irgendwie fast immer wie kurz vor dem Verhungern.
Bei vollem Gain (Attack) und leicht zurückgedrehten Bässen ließ sich aber doch eine definierte bis kernige Distortion bei den Akkorden erreichen, es bröckelt auch ein wenig, aber die Transparenz und das schöne Sägen des Germanium-Fuzz erreichte das Gerät nicht.
Unterhalb eines Levels von Vollverzerrung, d. h. im Bereich zwischen Clean und Distortion, gibt es keinen „Übergang“ in die Verzerrung – mit lauter werdendem Clean mischt sich nur zunehmend ein hässliches, weil außerhalb des musikalischen Kontext stehendes, Kratzen in den Ton. Eine Verbesserung brachte die Vergrößerung des Kollektorwiderstands und eine Verringerung der Ruhespannung am Kollektor von T2 auf übliche 4,5 V. Das Kratzen war schien etwas weniger spitz zu sein, störte aber weiterhin.
Insofern klang es, interessanterweise und anders als beim „Germanium-Fuzz“, mit „symmetrischen“ Arbeitspunkt besser.
Nochmal nachdenken
Zum Verlust des Gain gibt es, zumindest in Bezug auf T1, eine Idee – die T1 vorgeschaltete Diode bildet mit der Basis-Emitter-Strecke von T1 einen Spannungsteiler, der für den Gainverlust verantwortlich sein könnte. Der Spannungsteiler kommt durch die verschiedenen differentiellen Widerstände der p-n-Übergänge von T1 und der Diode zustande, wobei die Emulation des Reststroms über T3 das ganze noch verschlimmbessert haben könnte.
Um das abschätzen zu können, wurde zunächst der differentielle Eingangswiderstand von T1 betrachtet, d. h. in obiger Tabelle 1 noch die rechte Spalte mit dem berechneten Wert für ΔUB / ln(ΔIB2 / IB1) eingefügt. Dieser Wert gibt an, um wieviel die Basis-Emitter-Spannung bei der Erhöhung des Basisstroms um den Faktor e gestiegen ist. Diese Berechnung steht im Zusammenhang mit der Shockley-Gleichung, die die Beziehung von Durchlassstrom und Spannungsabfall an einem p-n-übergang beschreibt – hieraus lässt sich die Größe des differentiellen Widerstands bei einem bestimmten Basisruhestrom ableiten.
Um erkennen zu können, wie sich daraus der differentielle Widerstand einer Diode etc. bestimmt, eine kurze Herleitung. Zunächst die Shockley-Gleichung, bezogen auf eine Diode:
\( \begin{eqnarray} I_{\textrm{Diode}} & = & I_{\textrm{S}} \cdot \left( \exp{ \left( {\frac{U_{\textrm{Diode}}} {\eta \cdot U_{\textrm{T}}}} \right) } - 1 \right) \\~\\ & = & I_{\textrm{S}} \cdot \exp{ \left( {\frac{U_{\textrm{Diode}}} {\eta \cdot U_{\textrm{T}}}} \right) } - I_{\textrm{S}} \tag{1}\end{eqnarray} \)
Zur Gleichung: Bei UT = 26 mV handelt es sich um die sogenannte Temperaturspannung – sie ist von der Beschaltung unabhängig, steigt aber proportional mit der (absoluten) Temperatur. Der Wert des Emissionskoeffizienten η ist unter anderem materialabhängig und bewegt sich bei Siliziumdioden im Bereich unter zwei. Der Strom IS wiederum ist der sogenannte Sättigungssperrstrom, er liegt im Allgemeinen im Bereich von Pico- bis Nanoampere.
Obige Gleichung 1 wird nach Strömen und Spannungen aufgelöst:
\( \begin{equation} \cfrac{I_{\textrm{Diode}} + I_{\textrm{S}}} {I_{\textrm{S}}} = \exp{ \left( \cfrac{U_{\textrm{Diode}}} {\eta \cdot U_{\textrm{T}} } \right) } \tag{2}\end{equation} \)
es werden die Seiten vertauscht und die Gleichung wird logarithmiert:
\( \begin{equation} \cfrac{U_{\textrm{Diode}}} {\eta \cdot U_{\textrm{T}}} = \ln\left( \cfrac{I_{\textrm{Diode}} +I_{\textrm{S}}} {I_{\textrm{S}}} \right) \tag{3}\end{equation} \)
Um den differentiellen Widerstand der Diode zu ermitteln, muss uDiode nach iDiode (kleine Buchstaben, da temporäre Werte) abgeleitet werden. Der Wert für den Sättigungssperrstrom IS, ein Parameter des Bauelementes bzw. von dessen Basis-Emitter-Strecke, verschwindet durch die Multiplikation von äußerer und der innerer Ableitung beim Differenzieren:
\( \begin{eqnarray} \frac{d\,u_{\textrm{Diode}}} {d\,i_{\textrm{diode}}} & = & \eta \cdot U_{\textrm{T}} \cdot \frac{I_{\textrm{S}}} {I_{\textrm{Diode}}+I_{\textrm{S}}} \cdot \frac{1}{I_{\textrm{S}}} \\~\\ & = & \frac{\eta\cdot{}U_{\textrm{T}}} {I_{\textrm{Diode}}+I_{\textrm{S}}} \tag{6}\end{eqnarray} \)
Nun kann für d uDiode / d iDiode der differentielle Widerstand rDiode und für die Temperaturspannung UT deren Wert 26 mV eingesetzt werden:
\( \begin{equation} r_{\textrm{Diode}} = \cfrac{1} {I_{\textrm{Diode}}+I_{\textrm{S}}} \cdot\eta \cdot 26\,\Omega{} \tag{7}\end{equation} \)
Was bedeutet das? Wird eine Diode von einem Gleichstrom und einem Signalstrom durchflossen, so gilt für das Kleinsignalverhalten (d. h. die (Signal)stromänderungen sind kleiner als der Gleichstrom) einen nahezu linearen Zusammenhang zwischen der Größe des Gleichstroms und dem differentiellen- bzw. dem Signalwiderstand der Diode – die Größe des Widerstands verhält sich reziprok zur Größe des Gleichstroms.
Für eine der üblichen Kleinsignaldioden (1N4148, 1N4007, η kleiner als 2) ergibt sich ein differentieller Widerstand von etwa 50 Ω · 1 mA bzw. 50 kΩ · 1 µA.
Bei den gemessenen Leistungstransistoren bewegte sich der Quotient UBE / ln(ΔIB2 / IB1) bei etwa 30 mV, hier ist also mit einem differentiellen Widerstand der Basis-Emitter-Strecke von etwa 30 Ω · 1 mA bzw. 30 kΩ · 1 µA im Arbeitspunkt zu rechnen. In der konkreten Schaltung hat T1 insgesamt einen Basisruhestrom (simulierter Reststrom durch R15 und „normaler“ Basisstrom durch R1 von) etwa 3 µA. Entsprechend ergibt sich für T1 ein differentiellen Eingangswiderstand von etwa 9 kΩ.
Bei der Schottky-Diode 1N5817 ist die Abschätzung schwieriger. Sie wird von einem Ruhestrom von etwa 1 µA durchflossen. Sie hat allerdings, laut dem in Modell in LTSPICE, einen Strom IS von etwa 30 µA (wodurch die Abschätzung des differentiellen Widerstands nach der oben skizzierten Methode schwierig ist). In der Kennliniensimulation in genanntem LTSPICE hingegen ergibt sich ein differentieller Widerstand von etwa 1 kΩ bei einem Ruhestrom von 1 µA.
So gesehen ergibt sich ein Spannungsteiler von 9 kΩ zu 9 kΩ plus 1 kΩ – das erklärt jetzt nicht unbedingt den Verlust an Gain.
Nachtrag
Später konnten zwei Dioden 1N5817 mit einem selbstgebauten primitiven Helferlein zur genauer durchgemessen und deren ungefähre Kennlinien bestimmt werden. Es ergab sich ein Sperrstrom IS von etwa 0,6 µA und ein Emissionskoeffizient von etwa eins.
In obiger Schaltung ergibt sich für bei einem Strom von 1 µA durch D1 ein differentieller Widerstand von etwa 15 kΩ (26 mV, geteilt durch Diodenstrom plus Sperrstrom), der bei geringerem Diodenstrom bis maximal 40 kΩ ansteigen kann (26 mV, geteilt durch Sperrstrom). Somit ist der Verlust an Gain dann doch nachvollziehbar.
Ausblick
Insgesamt muss allerdings konstatiert werden, dass der Ansatz, möglichst niedrigverstärkende Leistungstransistoren zu verwenden, um die rauschenden „Low-Gain-Germaniumtransistoren“ zu ersetzen, keinen Erfolg hatte. Der nächste Schritt besteht darin, zumindest T1 nicht auf einen extrem niedrigen Stromverstärkungsfaktor von etwa 30 „zu trimmen“, sondern einen Transistor mit höherer Verstärkung zu verwenden. Möglicherweise ist es sinnvoll, den ganzen Versuch mit anderen Transistoren mit etwas größerem Gain (z. B. mit einem Transistorarray CA3046) zu wiederholen.
