Surfy Industries
Surfy Trem und Surfy Vibe
Röhrenersatzvibrato Surfy Vibe – LFO und Filter
Kapitelinhalt:[ Überspringen ]Der LFO
Die Schaltung des Effekts Surfy Industries Surfy Vibe soll sich dem Vernehmen nach an der Schaltung (bzw. dem Vibratoeffekt) eines alten „Magnatone“-Verstärkers orientieren. Will man eine solcherart in einem Effektgerät adaptierte Schaltung nachvollziehen, so ist es sinnvoll, sich die Originalschaltung anzuschauen. Der folgende Schaltplan 3.1 zeigt den LFO, die Filterschaltung und den Bias-Treiber im Verstärker „Magnatone 280B“:


Schaltplan 3.1: LFO, Filter und Biastreiber im Magnatone 280B – die Stereofunktion wurde in obigem Schaltplan nicht berücksichtigt. Gezeichnet nach Vorlage aus [ magnatone ] – Bauteilenumerierung „freihändig“.
Eine kurze Beschreibung: Auf eine „klassische“ LFO-Schaltung (linke Triode) folgen ein Volumenregler, ein per Fußschalter (oder den Ringkontakt der Eingangsklinkenbuchse) schaltbarem Massekurzschluss (der LFO ist „immer an“, sein Ausgangssignal wird nur bei Bedarf gegen Masse gezogen), ein doppelter Tiefpass ( −3db-Frequenz etwa 100 Hz; es werden nur die scharfen Kanten aus dem LFO-Signal herausgefiltert) und eine Symmetrierschaltung (ein Röhrenstufe mit gleichen Kathoden- und Anodenwiderständen, deren Gitterruhespannung / Arbeitspunkt über einen Eingangsspannungsteiler 10 MΩ auf 3,3 MΩ auf etwa ein Viertel bzw. drei Viertel der Betriebsspannung an Kathode bzw. Anode festgelegt wird.) Interessant hier ist, dass dem Kathoden- und dem Anodenwiderstand jeweils ein Kondensator 250 nF parallelgeschaltet ist.
Nun zum Effektgerät – der folgende Schaltplan 3.2 zeigt die vermutete und auf dem Breadboard getestete Schaltung des LFO im Frequenz- und Kondensatorenmaßstab 1 / 100:
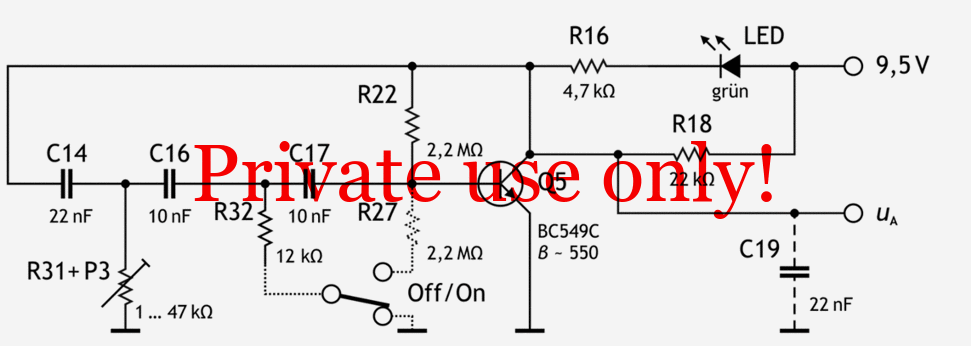

Schaltplan 3.2: Testschaltung für den LFO des Surfy Vibe. Mit den gepunkteten Linien wird der Einsatz des Fußschalters angedeutet – auf dem Breadboard lag R12 an Masse und R27 war nicht vorhanden.
Hier – wieder einmal – ein Erklärungsversuch:
- Transistor
-
Auf dem Breadboard wurde ein BC549C (mit einem β von voraussichtlich 550) verwendet. Es war nicht ganz klar, ob es sich beim Transistor Q5 um einen Standard- oder einen Darlington-Typ handelt (die Beschriftung des SMD-Transistors legt sowohl einen BC847 als SMD-Version des BC547 wie auch einen Darlingtontransistor MPSA06 nahe). Allerdings hat ein Darlingtontransistor hier die geringere Verstärkung – da sich die Verstärkung einer Stufe in Emitterschaltung in etwa aus dem Quotienten der Spannung über dem Kollektorwiderstand und der Temperaturspannung des Basis-Emitter-pn-Übergangs ergibt, hat die Stufe mit dem Darlingtontransistor (mit zwei pn-Übergängen) unter gleichen Bedingungen eine geringere Verstärkung, wenn auch einen höheren Eingangswiderstand.
- Arbeitspunkt
-
Der Arbeitspunkt der Stufe in Ruhelage wird bestimmt durch einen Widerstand R22 = 2,2 MΩ zwischen Basis und Kollektor von Q5.
- Ausgang
-
Zwischen Kollektor und der Betriebsspannung (9,5 V auf dem Breadboard) liegen ein Kollektorwiderstand R20 = 4,7 kΩ und eine grüne LED (es wurde eine grüne LED verwendet, um die etwas zu hohe Betriebsspannung auf dem Breadboard von 9,5 V ein wenig auszugleichen) sowie, parallel dazu, ein Widerstand R19 = 22 kΩ als Ersatz für den Trimmer R19 auf der Platine. Das Ausgangssignal wird am Kollektor von Q5 abgegriffen.
- Rückkopplungsschleife
-
Zwischen Kollektor und Basis von Q5 liegen drei Kondensatoren in Serie: C12 = 22 nF, C15 = 10 nF und C16 = 10 nF. Zwischen C12, C15 und Masse liegt ein in den Stufen der E3-Reihe einstellbarer Widerstand (1 kΩ, 2,2 kΩ … 47 kΩ), der die Serienschaltung aus SPEED-Regler P3 = 47 kΩ und R31 = 1 kΩ ersetzt, während die Verbindung von C15 und C16 über einen Festwiderstand R32 = 12 kΩ mit Masse verbunden wird.
- Maßstab der Kondensatoren
-
Im Surfy Vibe waren für C12, C15 und C16 Werte um 1 µF gemessen worden, wobei der erste Kondensator C12 ein wenig größer zu sein schien. Sinnvoll schien hier die Festlegung auf C12 = 2,2 µF sowie C15 = C16 = 1 µF – d. h. das Prinzip, dass der erste Kondensator doppelt so groß ist wie die anderen beiden, wird von Fender übernommen. Mit dem Einsatz von 22 nF, 10 nF und 10 nF wurde der „Maßstab der Kondensatoren“ für die Testschaltung auf eins zu hundert festgesetzt.
- Kapazitive Last
-
Zwischen Kollektor und der Masse liegt, wie auf der Platine des Effektgerätes gesehen, ein Kondensator 22 nF – (entsprechend 2,2 µF bzw. dem gemessenen Wert von 1,3 µF für C19) – die Schaltung des LFO wurde mit und ohne diesen Kondensator getestet.
- Fußschalter
-
Der Fußschalter (bzw. die Start-Stop-Schaltung) wurde in der Testschaltung auf dem Breadboard nicht berücksichtigt. Es scheint so, dass der Fußschalter in der Originalschaltung im Bypass-Fall zweierlei tut:
-
Mit einer Schalterebene wird die LED im Kollektorkreis, die zugleich die Status-LED des Gerätes ist, kurzgeschlossen.
-
Die andere Schalterebene trennt die Verbindung von R32 nach Masse und verbindet sie über einen Widerstand R30 = 2,2 MΩ mit der Basis von Q5, schließt also den letzten Phasenschieberkondensator C17 kurz und lädt C16 auf.
Damit wird zum einen der LFO deaktiviert; zum anderen werden bei dessen erneutem Aktivieren C16 und C17 umgeladen, wodurch der LFO wieder anspringt.
-
Diese „Fußschaltergeschichten“ (in obigem Schaltplan 3.2 gepunktet gezeichnet) wurden auf dem Breadboard nicht getestet.
-
Zu den Ergebnissen: Die in Schaltplan 3.2 skizzierte Testschaltung funktionierte auf dem Breadboard gut, die folgende Tabelle 3.1 listet die gemessenen Werte auf:
| R31+P1 [kΩ] |
ohne C19 | mit C19 | ||||
|---|---|---|---|---|---|---|
| f [Hz] |
uA,pp [V] |
f [Hz] |
uA,pp [V] |
|||
| pp | eff. | pp | eff. | |||
| 1 kΩ | 611 | 7,1 | 2,5 | 529 | 5,6 | 2 |
| 2,2 kΩ | 463 | 7,6 | 2,6 | 439 | 6,8 | 2,4 |
| 4,7 kΩ | 356 | 7,7 | 2,7 | 344 | 7,2 | 2,5 |
| 10 kΩ | 280 | 7,8 | 2,8 | 273 | 7,4 | 2,6 |
| 22 kΩ | 225 | 7,8 | 2,8 | 221 | 7,4 | 2,6 |
| 47 kΩ | 187 | 7,4 | 2,6 | 182 | 6,9 | 2,4 |
Die Werte (Ausgangspegel und Frequenz) noch einmal in einem kleinen Doppeldiagramm:
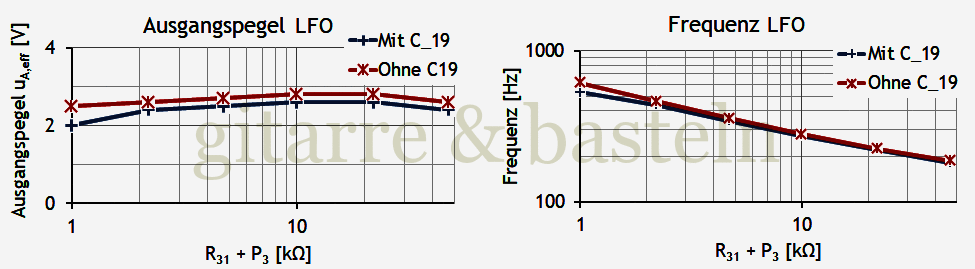

Diagramm 3.1: Darstellung der gemessenen Werte in der Testschaltung entsprechend Schaltplan 3.2 und Tabelle 3.1
Es zeigt sich, dass die Anbindung des Filterkondensators C19 an den Kollektor von Q5 natürlich Folgen hat (es wird mit dem Tiefpass RC / C19 ja auch in die Rückkopplungsschleife des LFO eingegriffen), aber kein großes Problem für die Funktion des LFO darstellt – die maximal mögliche Frequenz ist mehr als zehn Prozent kleiner und der dessen Ausgangspegel fällt bei großen Frequenzen um etwa 2 dB.
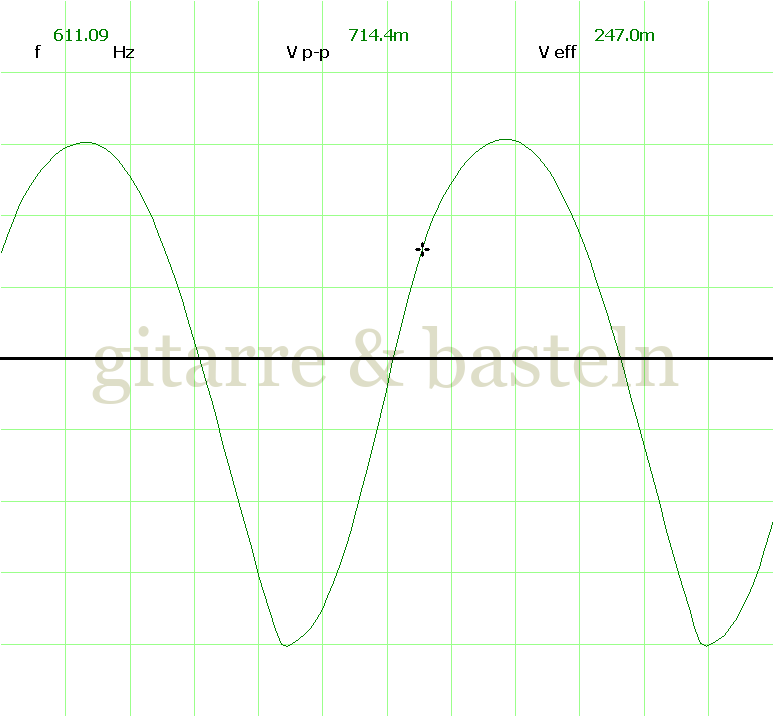
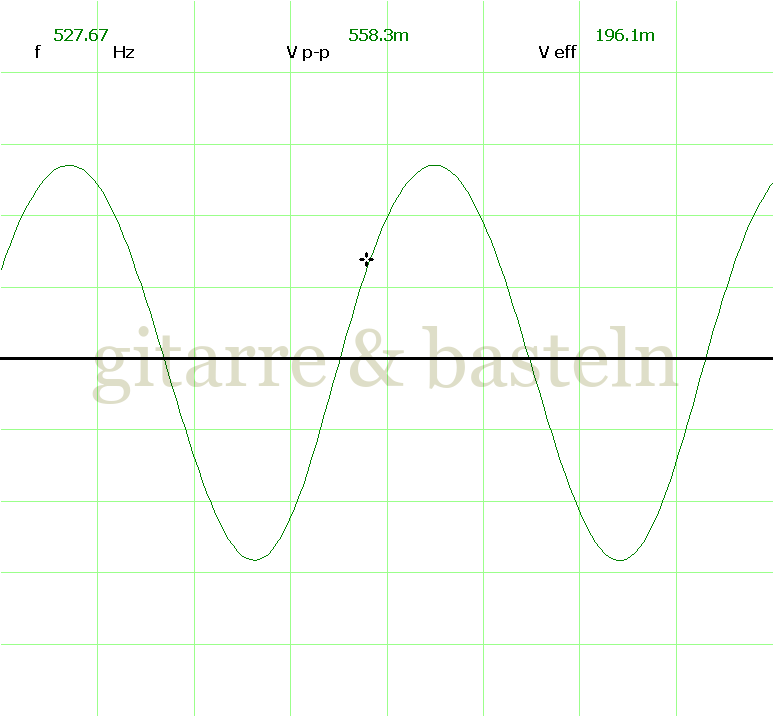
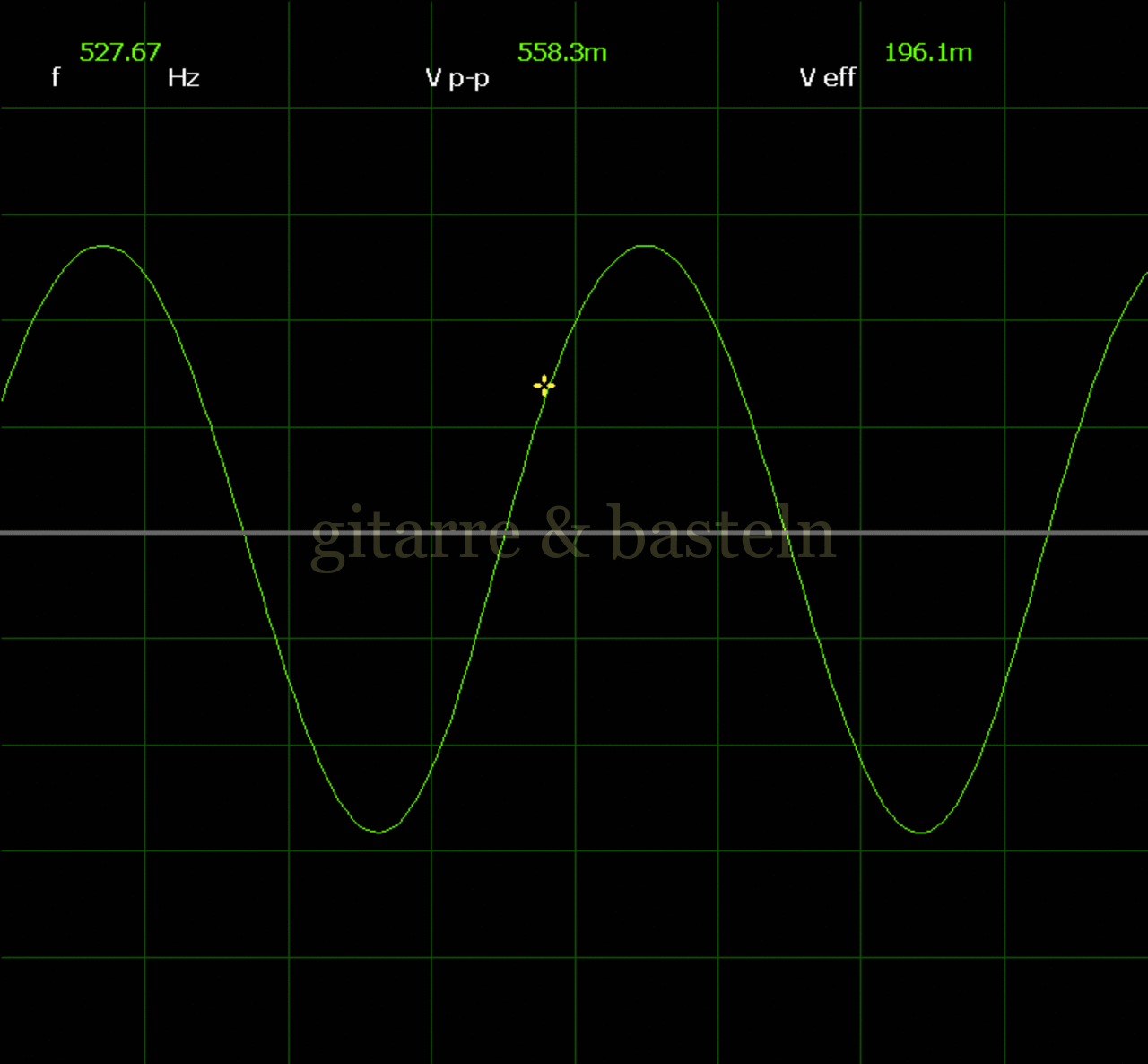
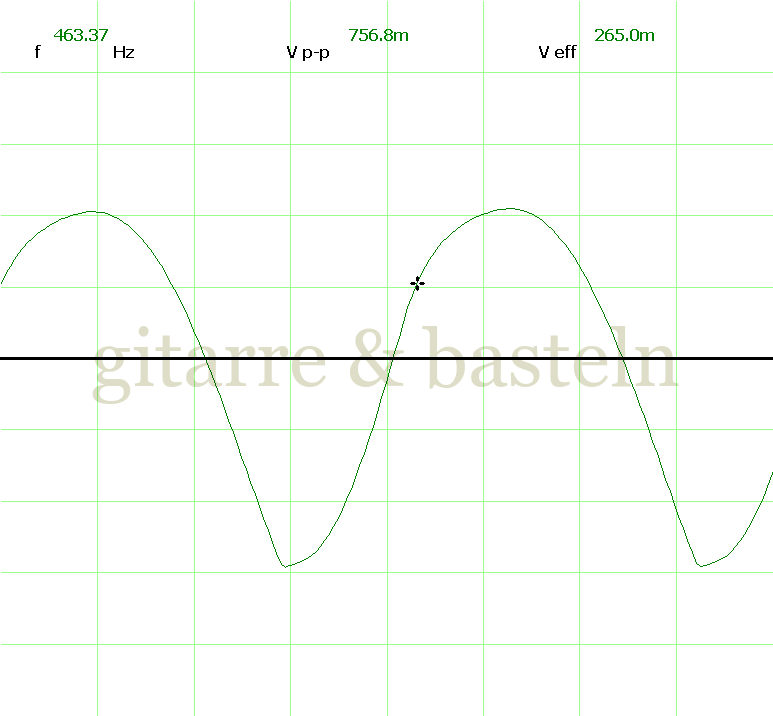
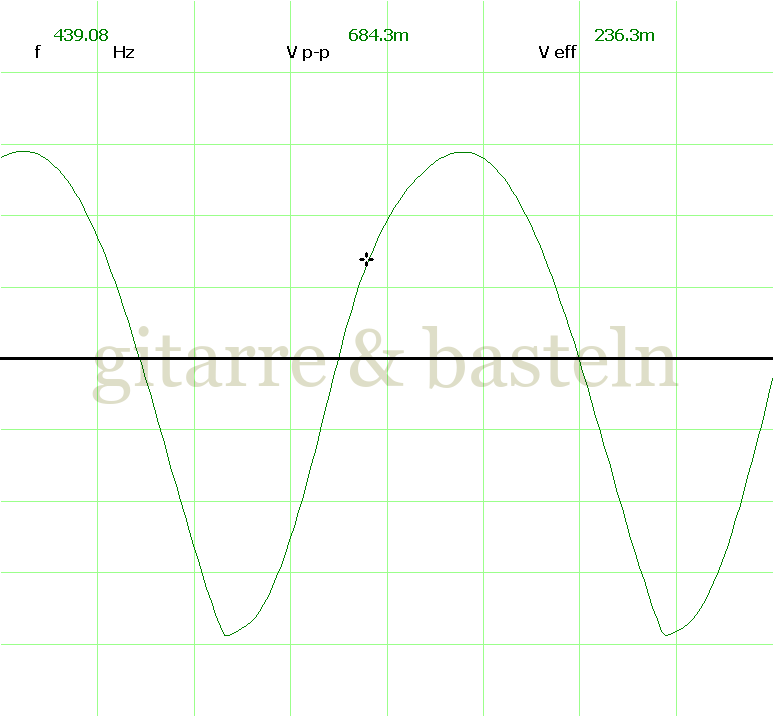
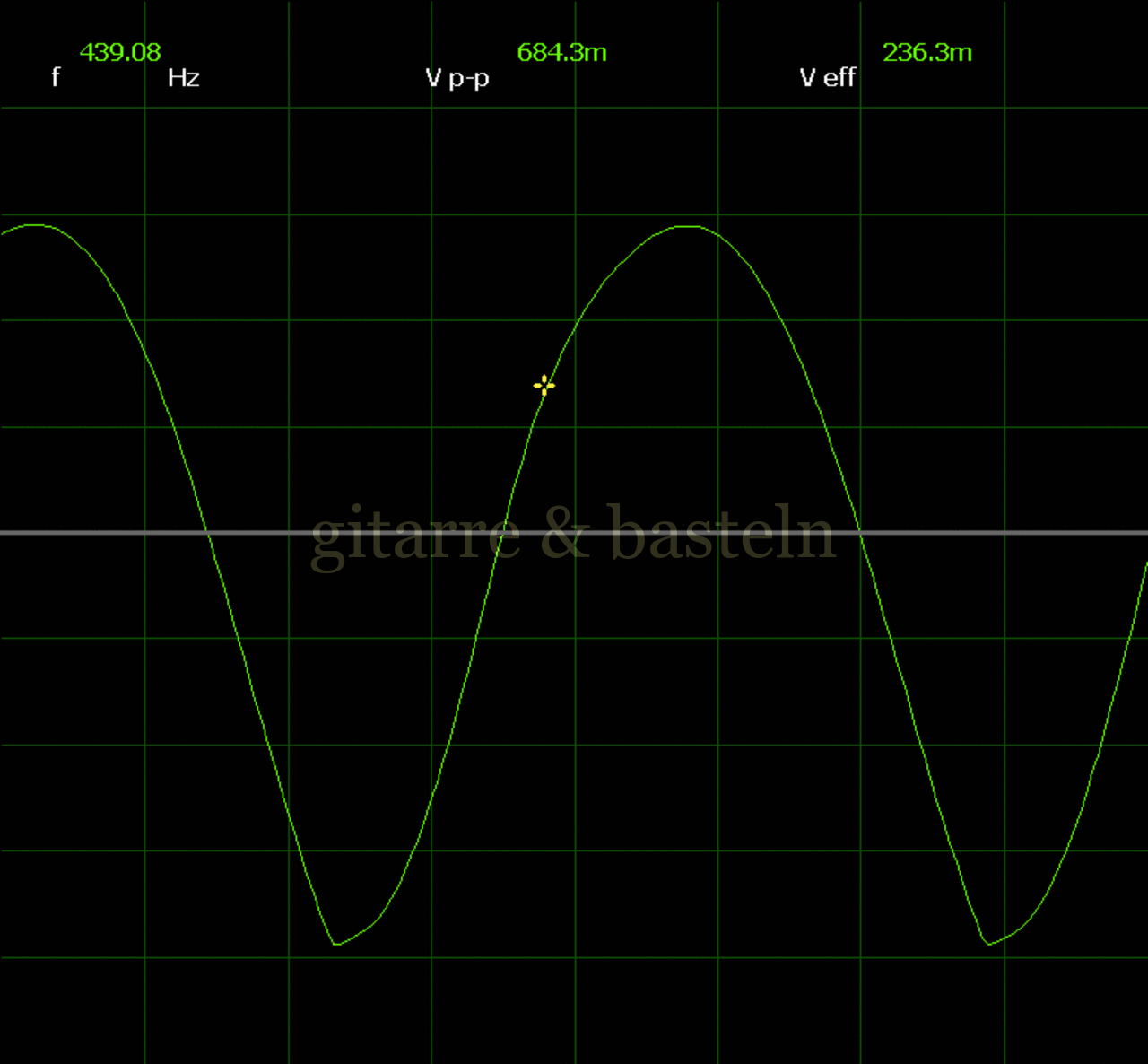
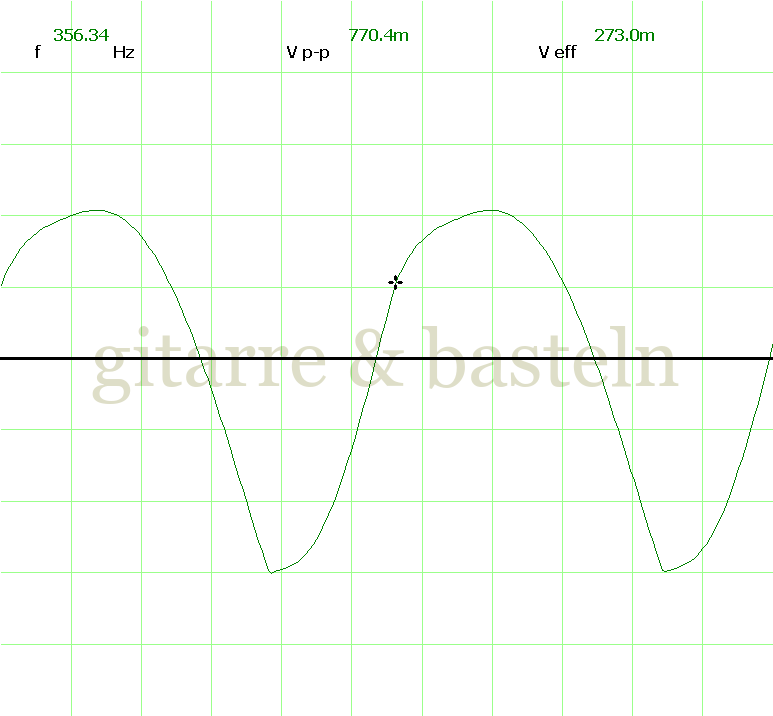
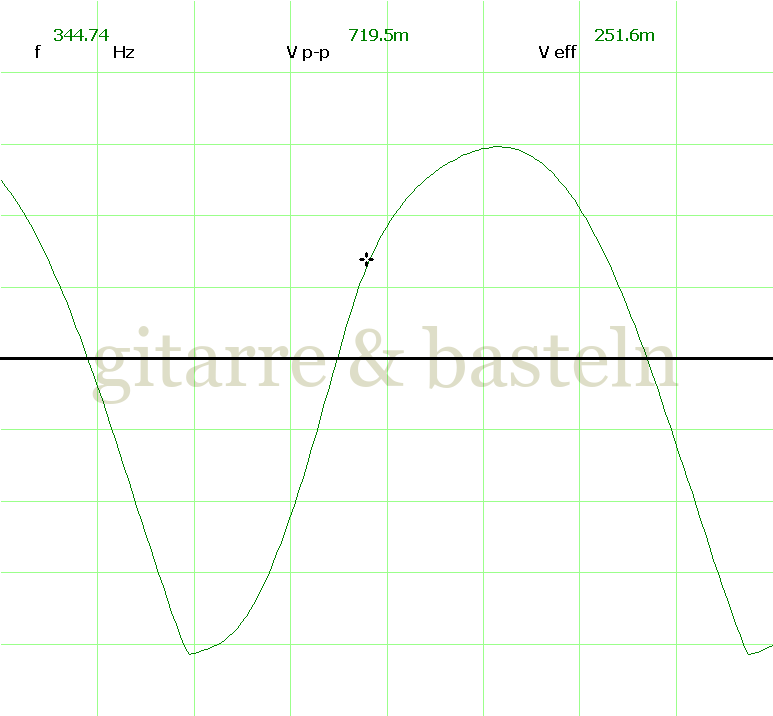
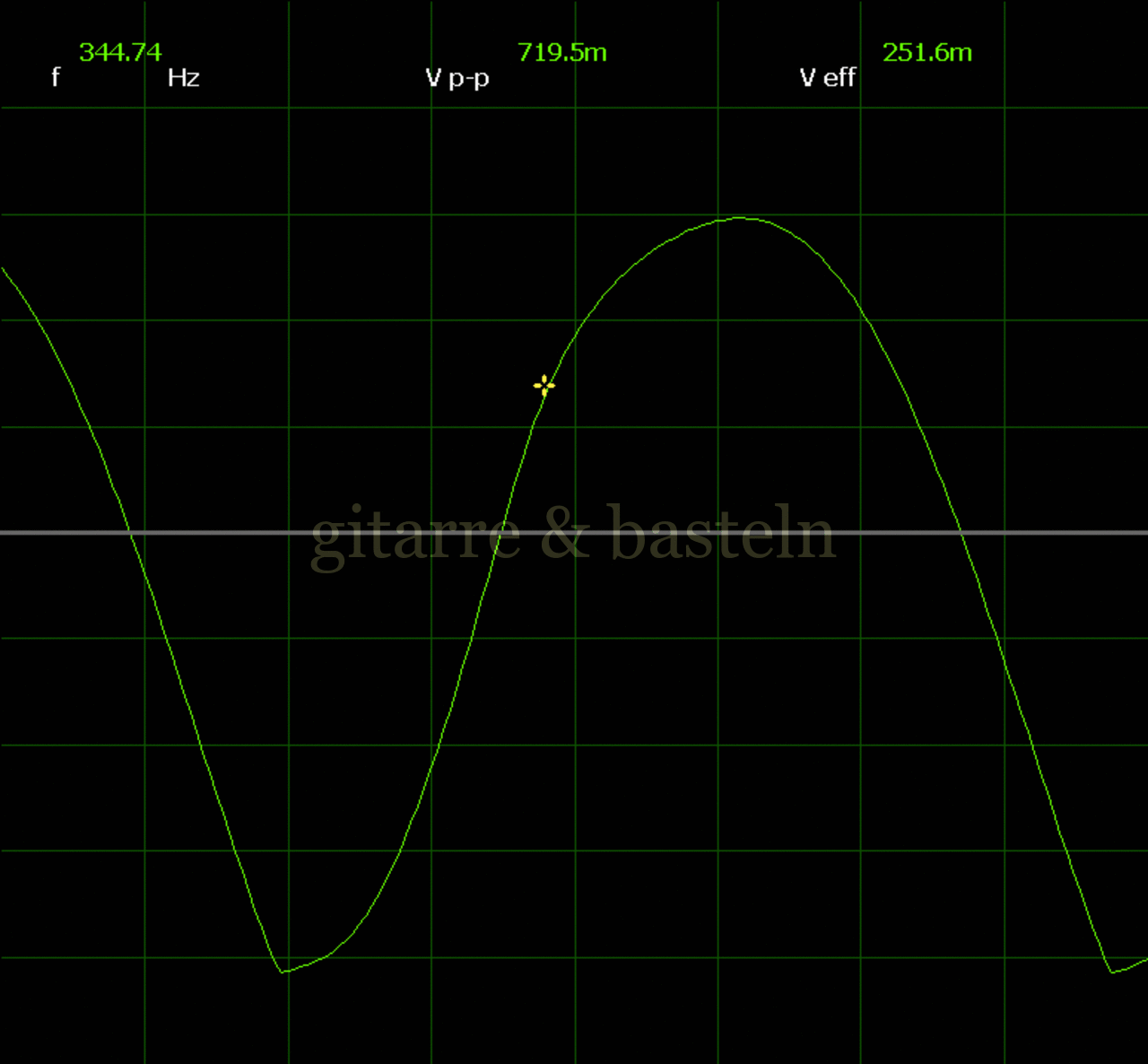
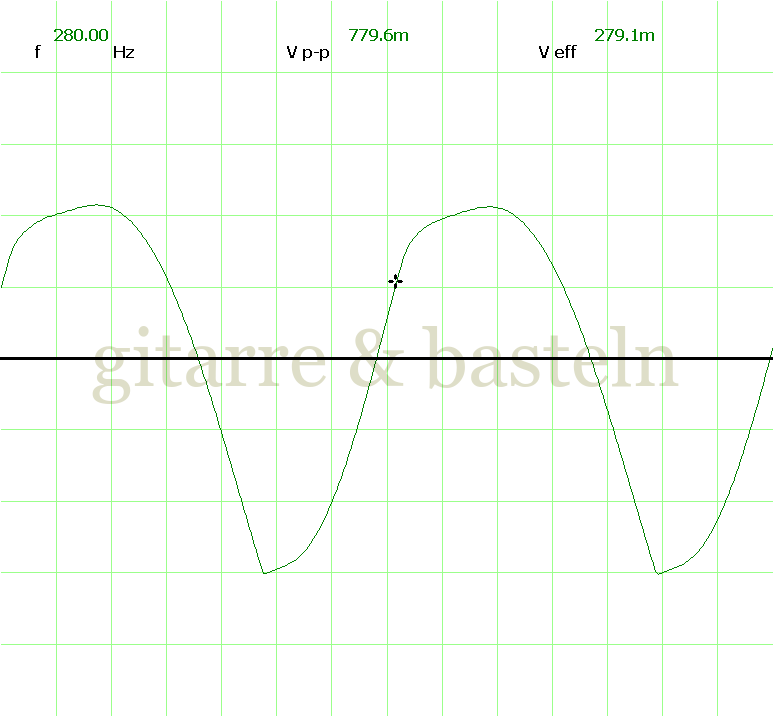
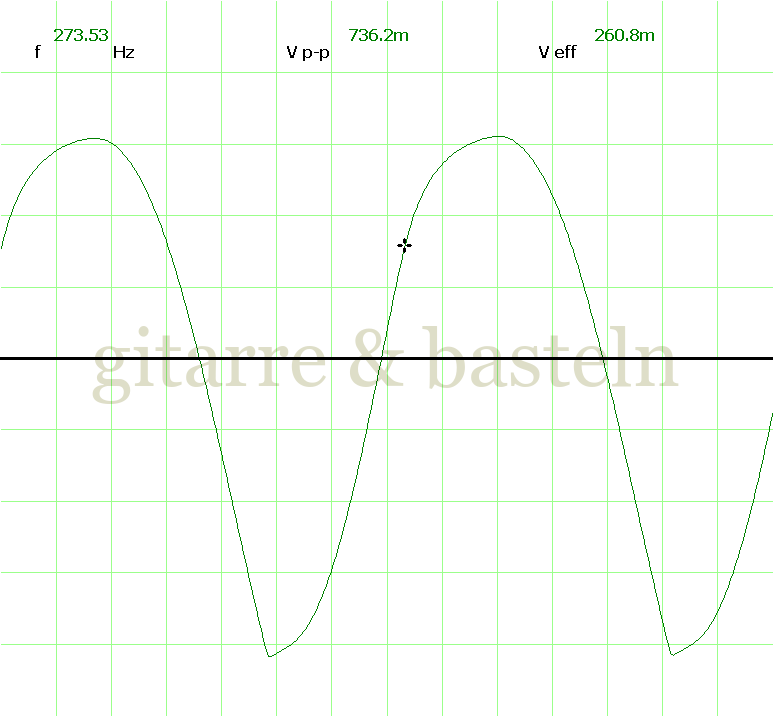
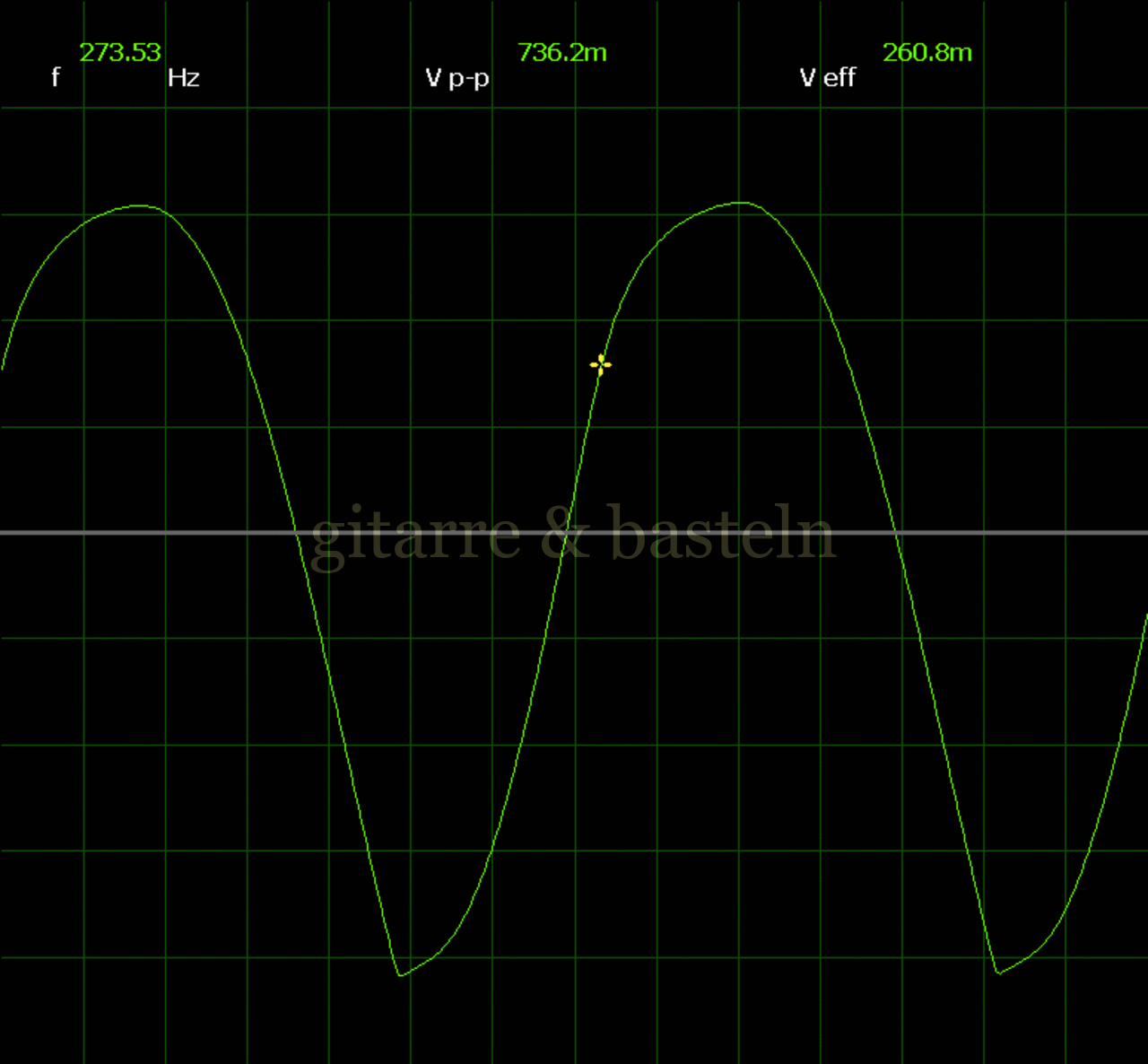
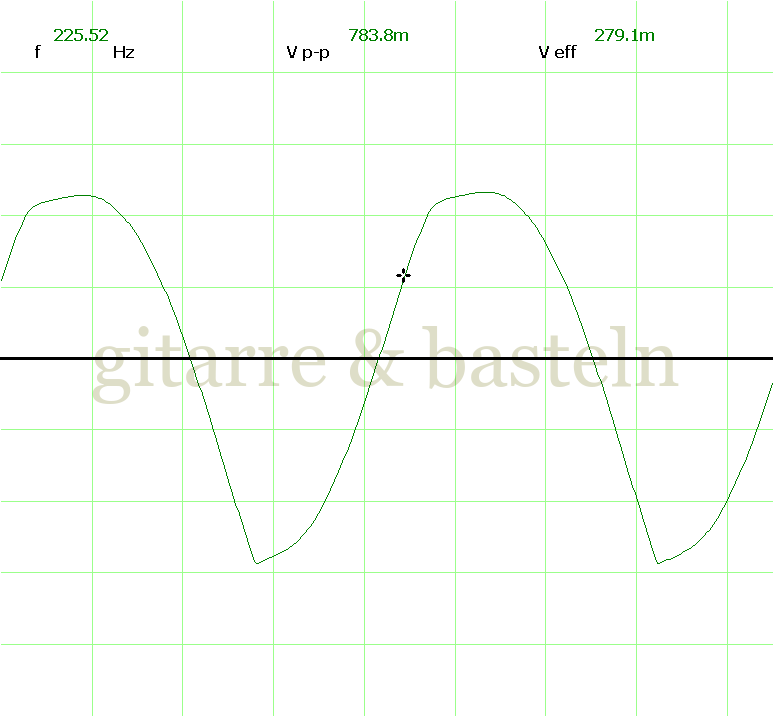
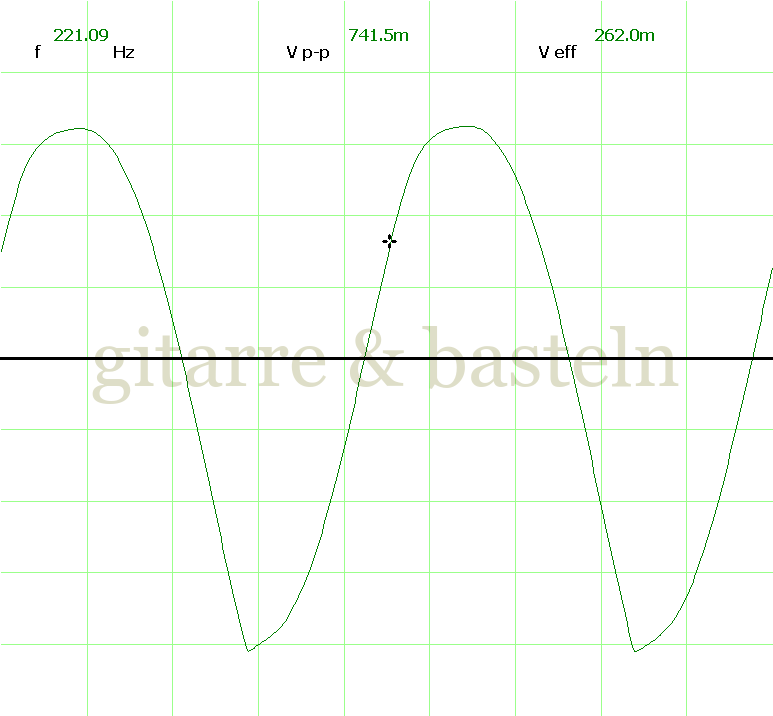
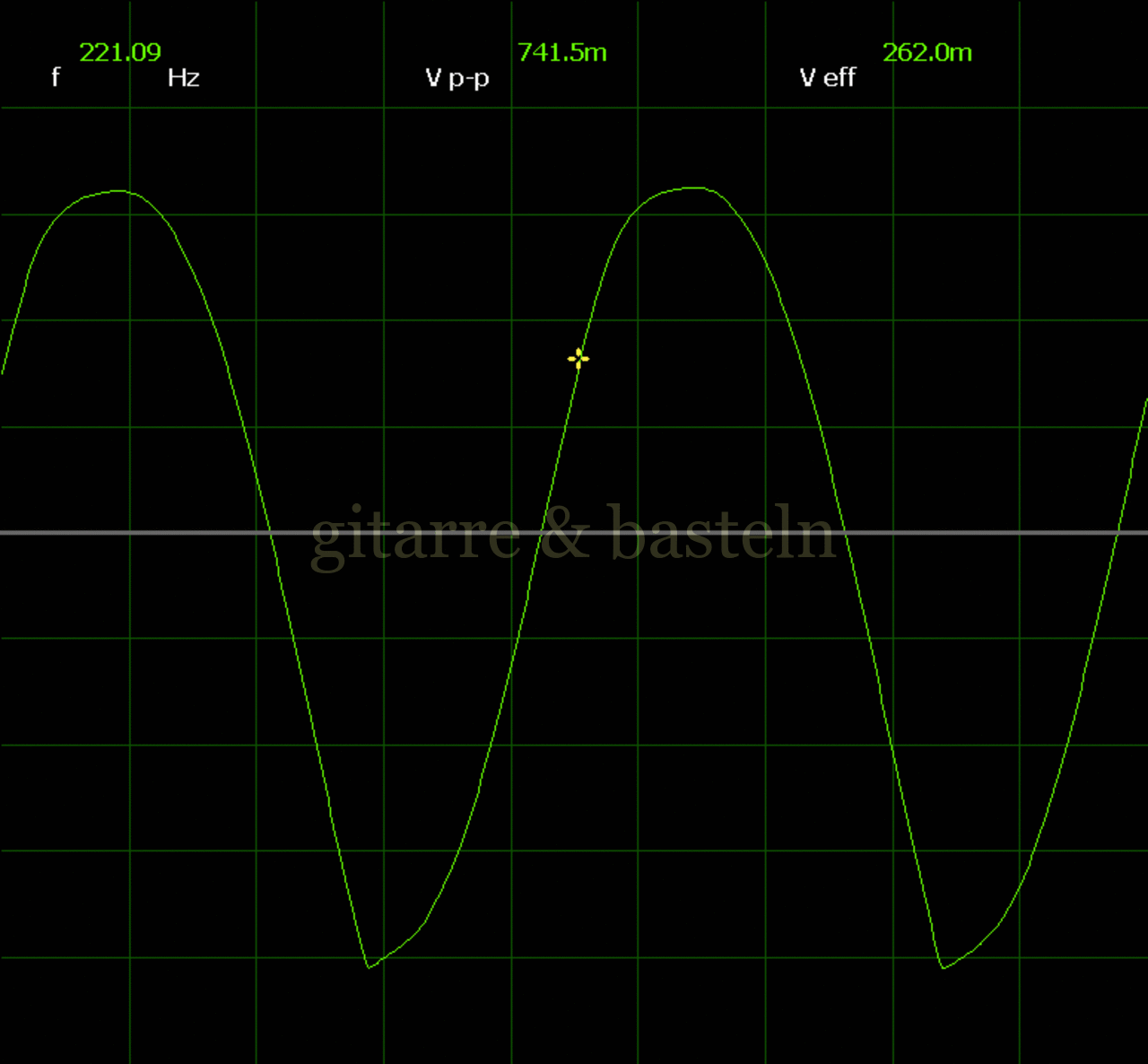
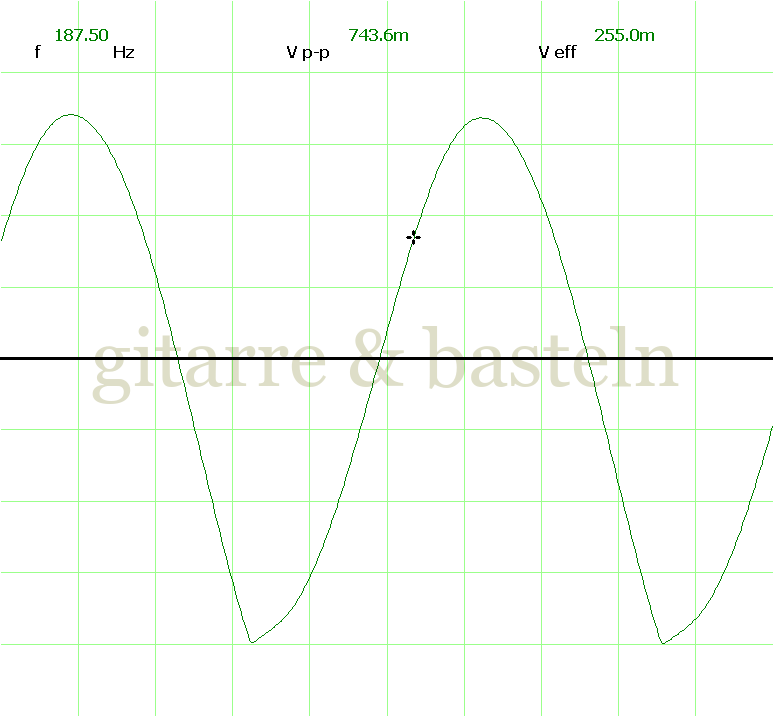
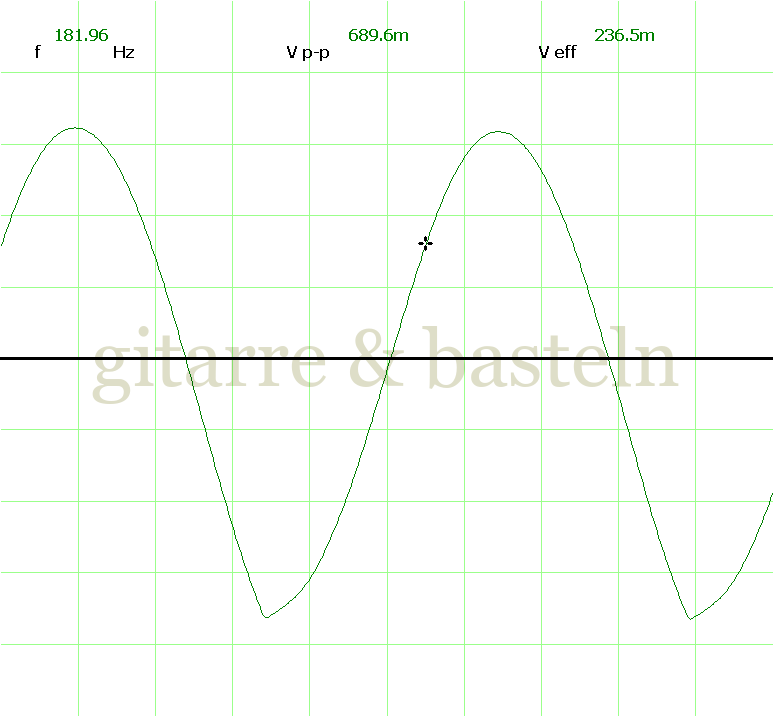
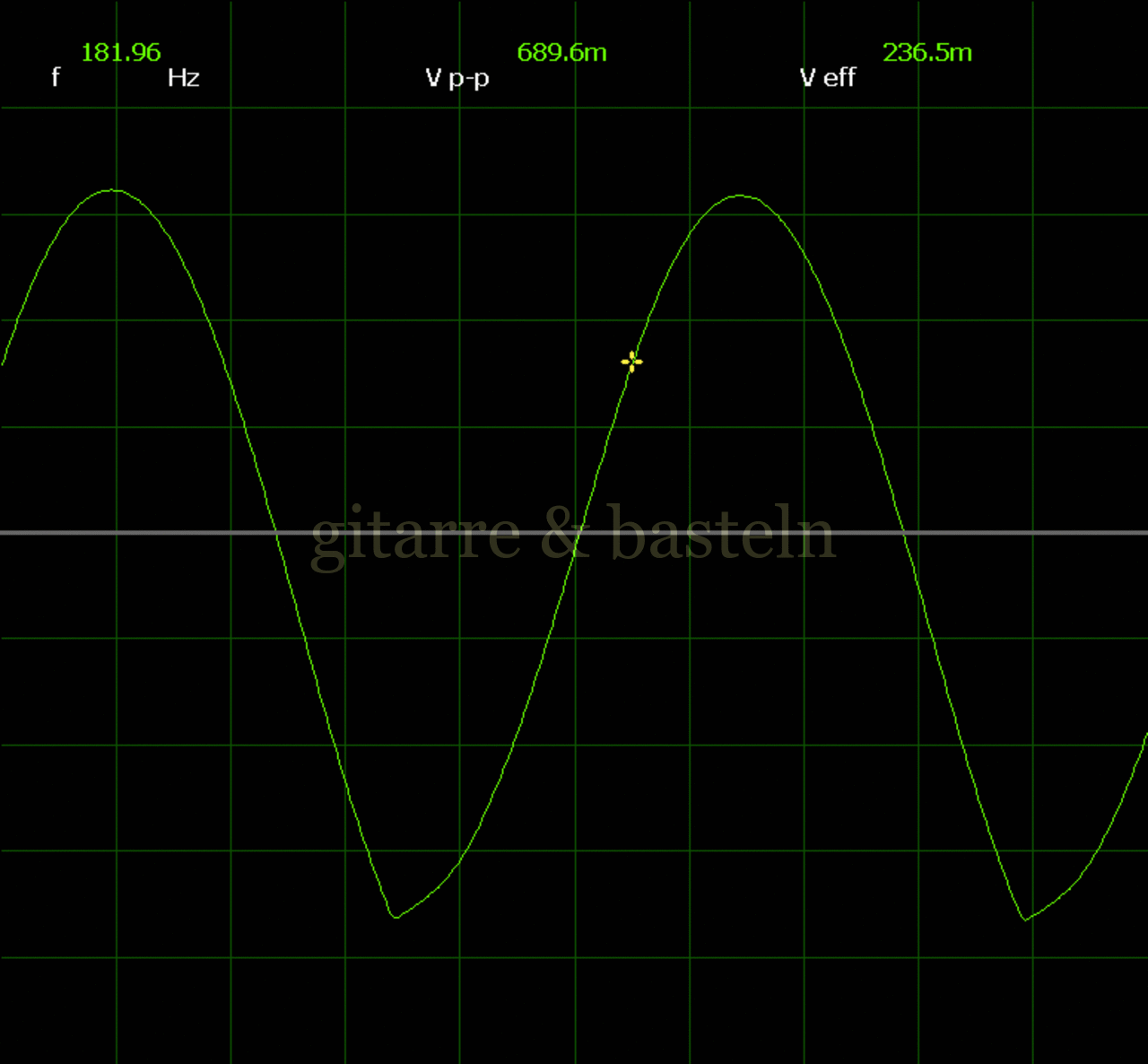
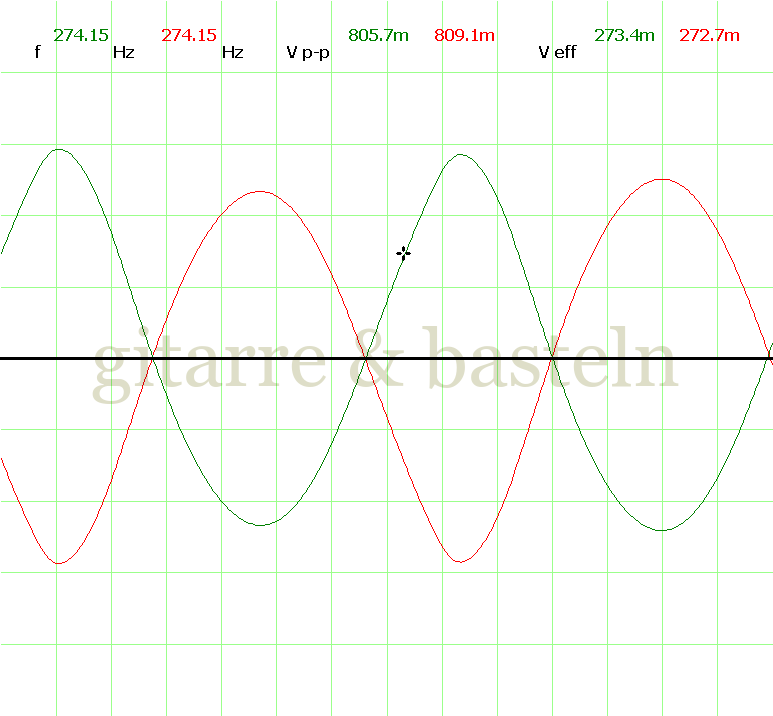
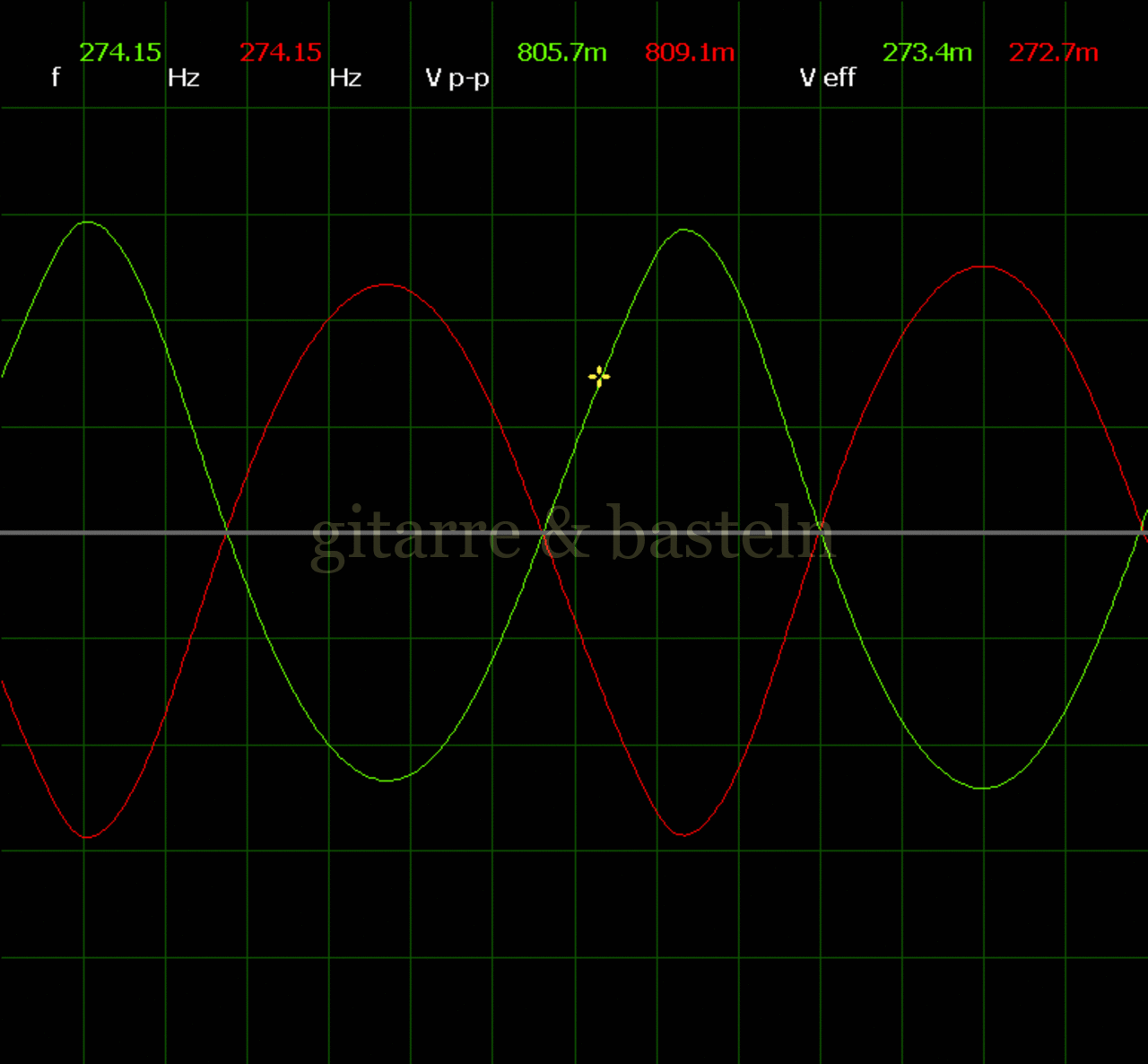
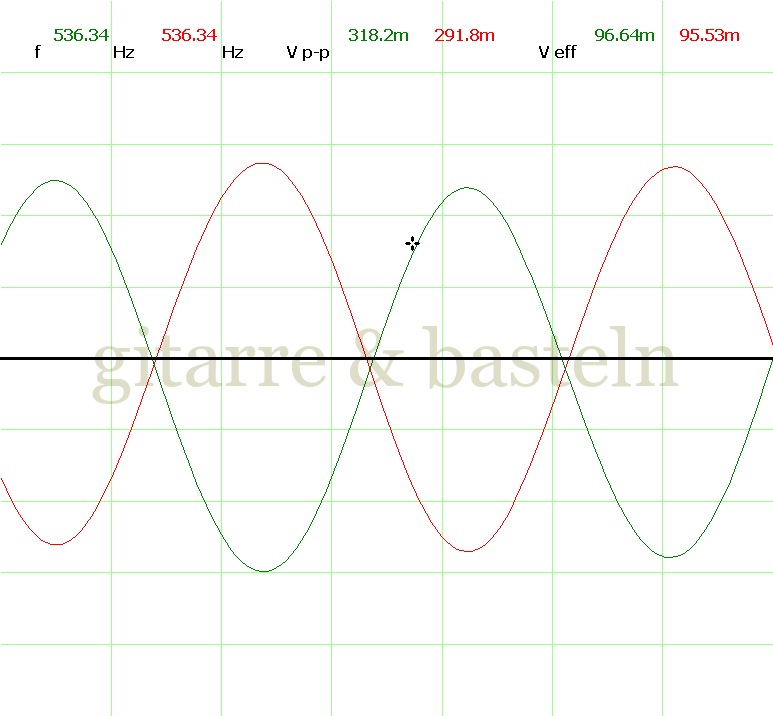
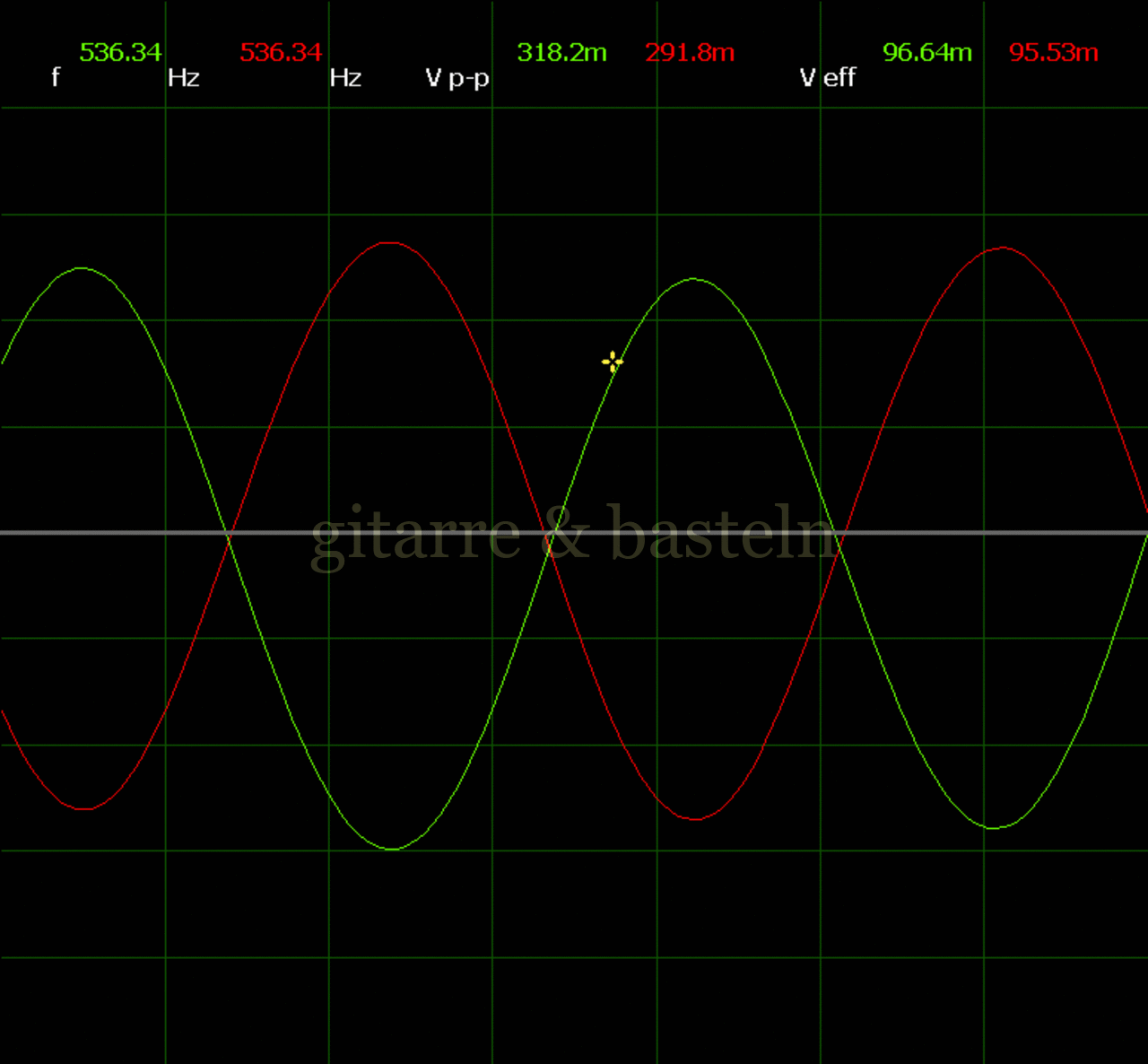
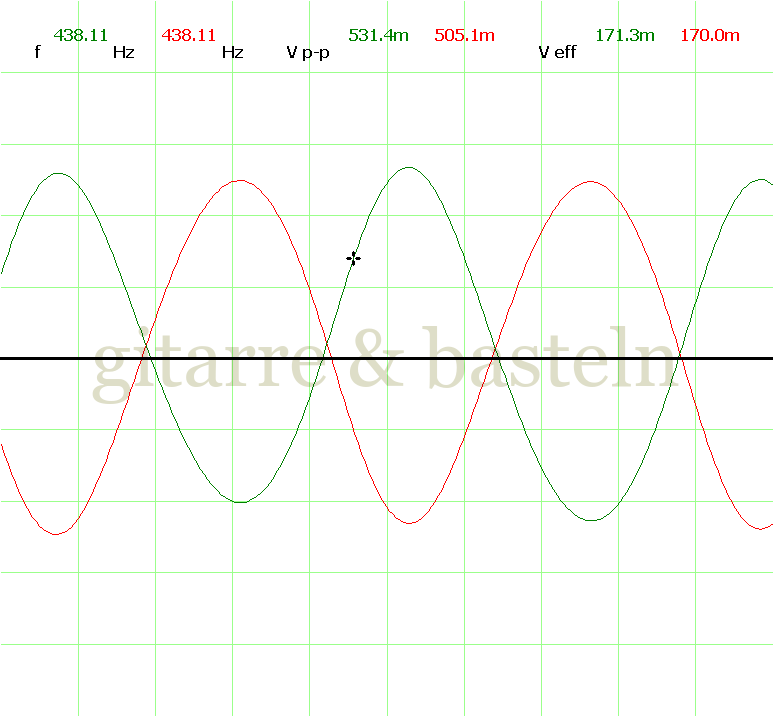
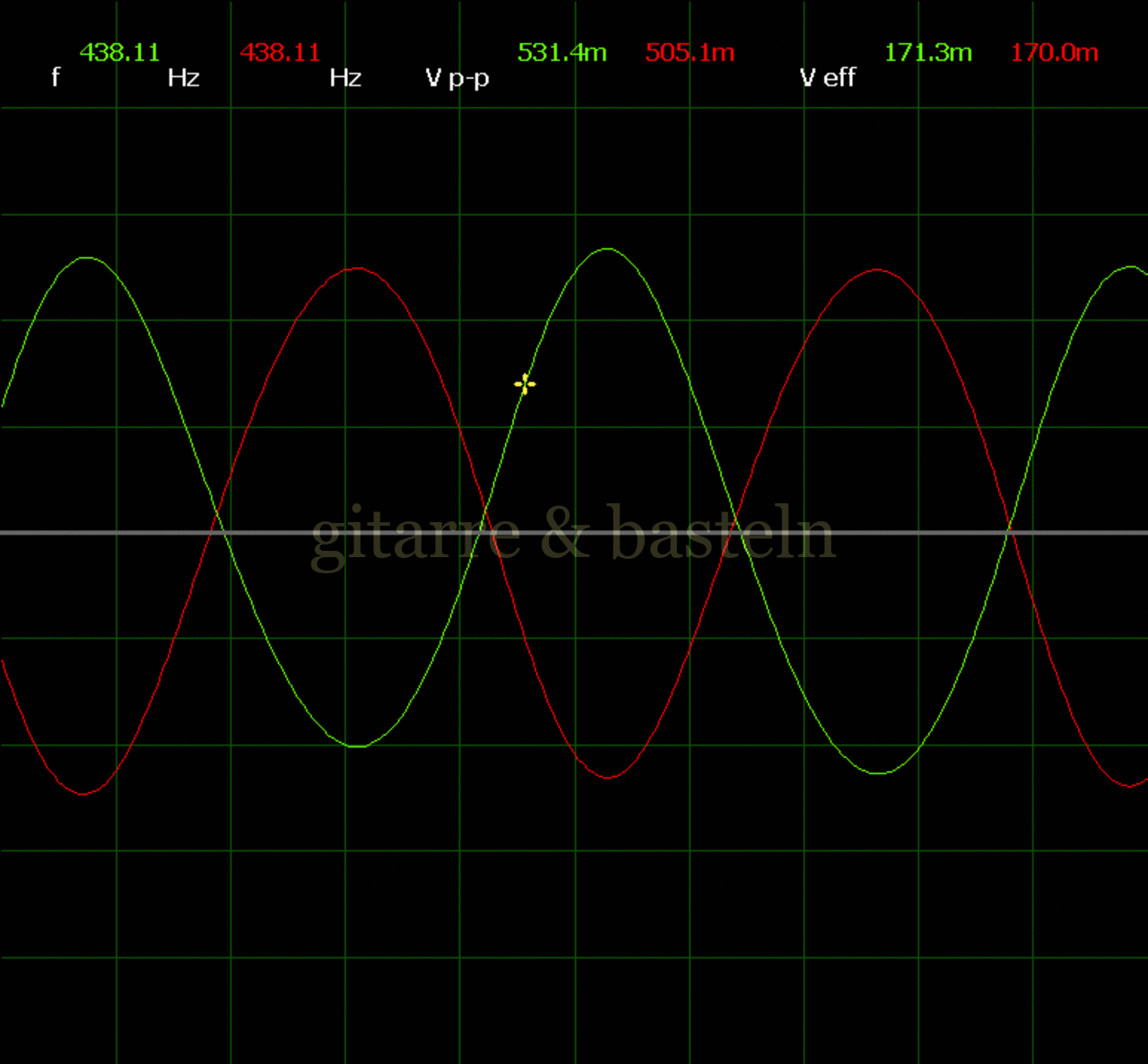
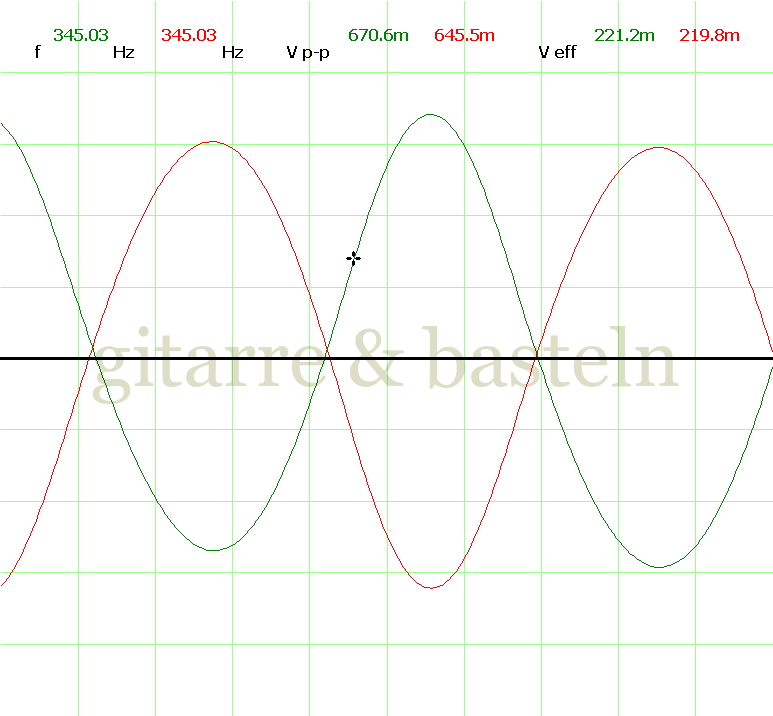
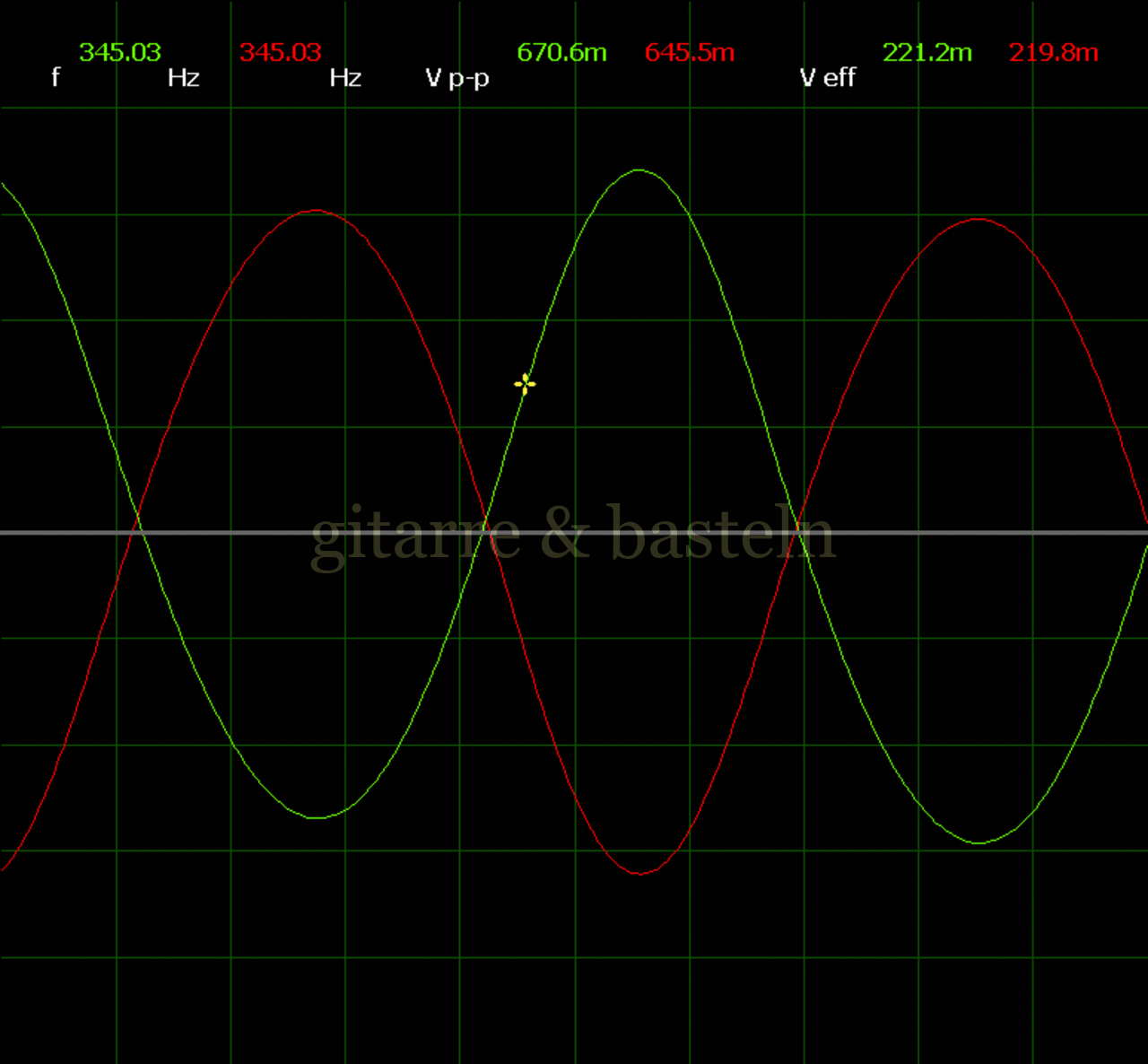
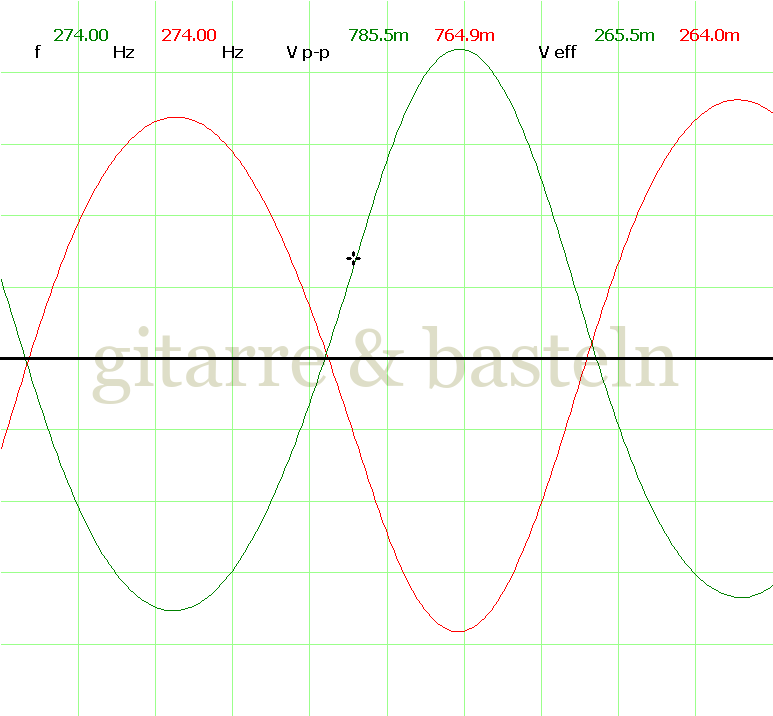
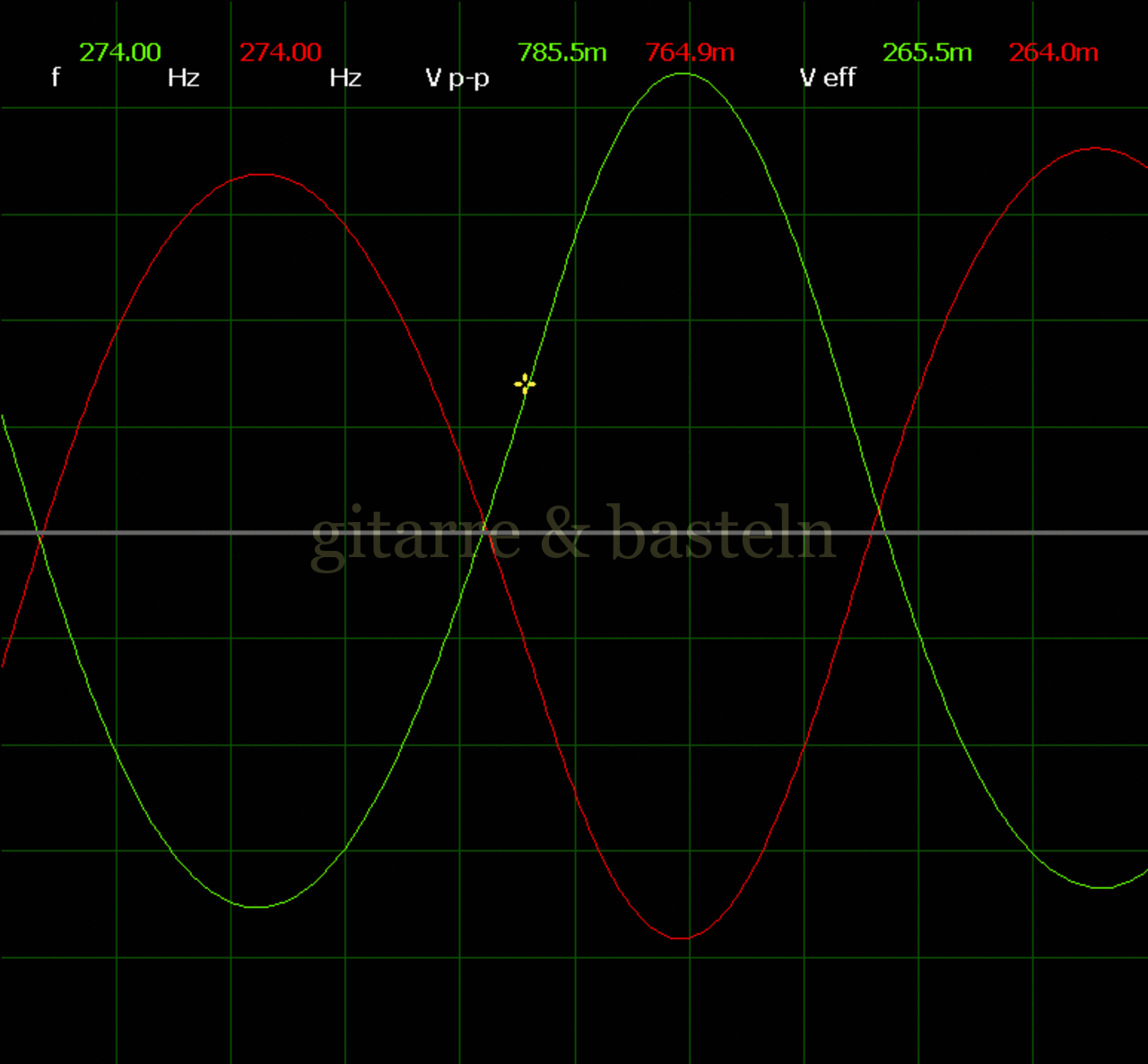
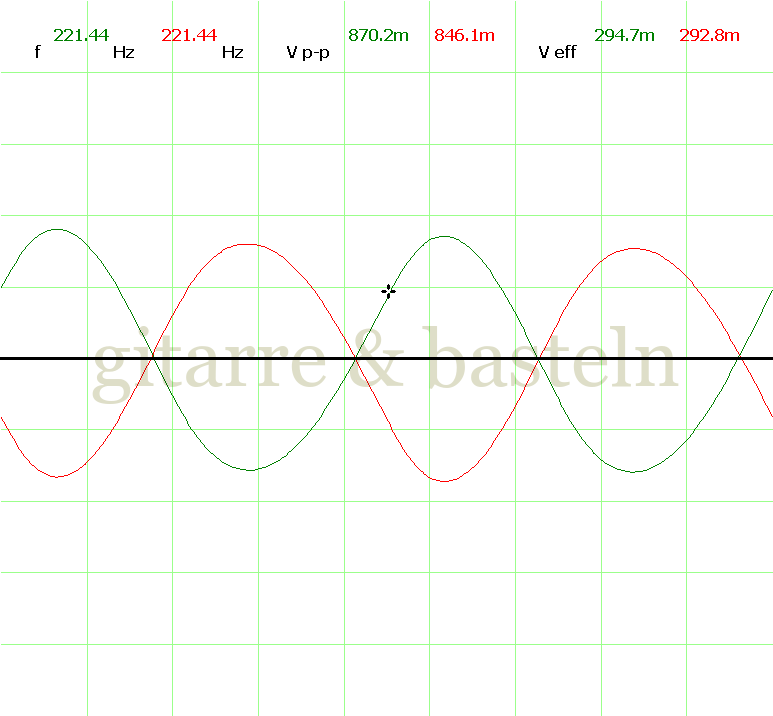
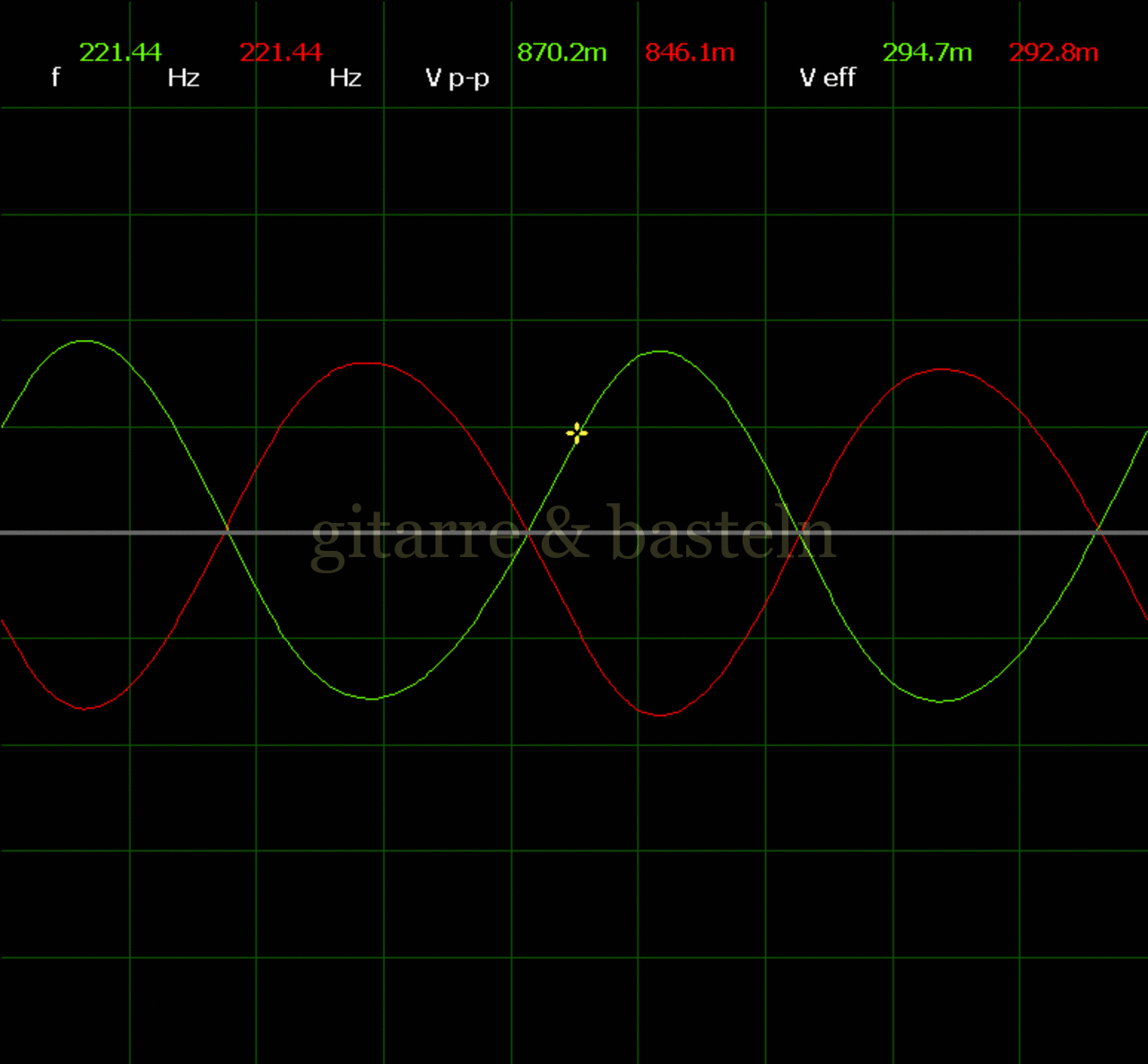
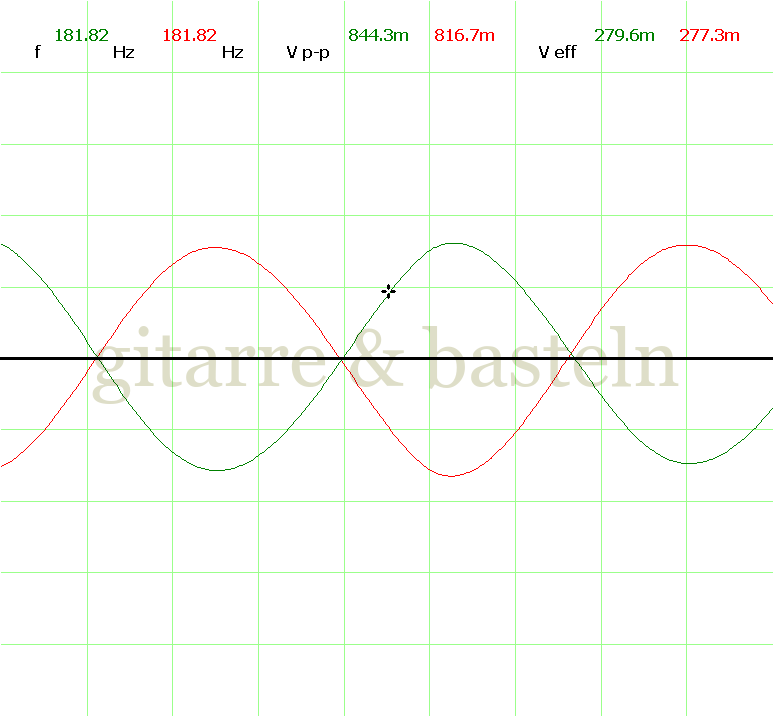
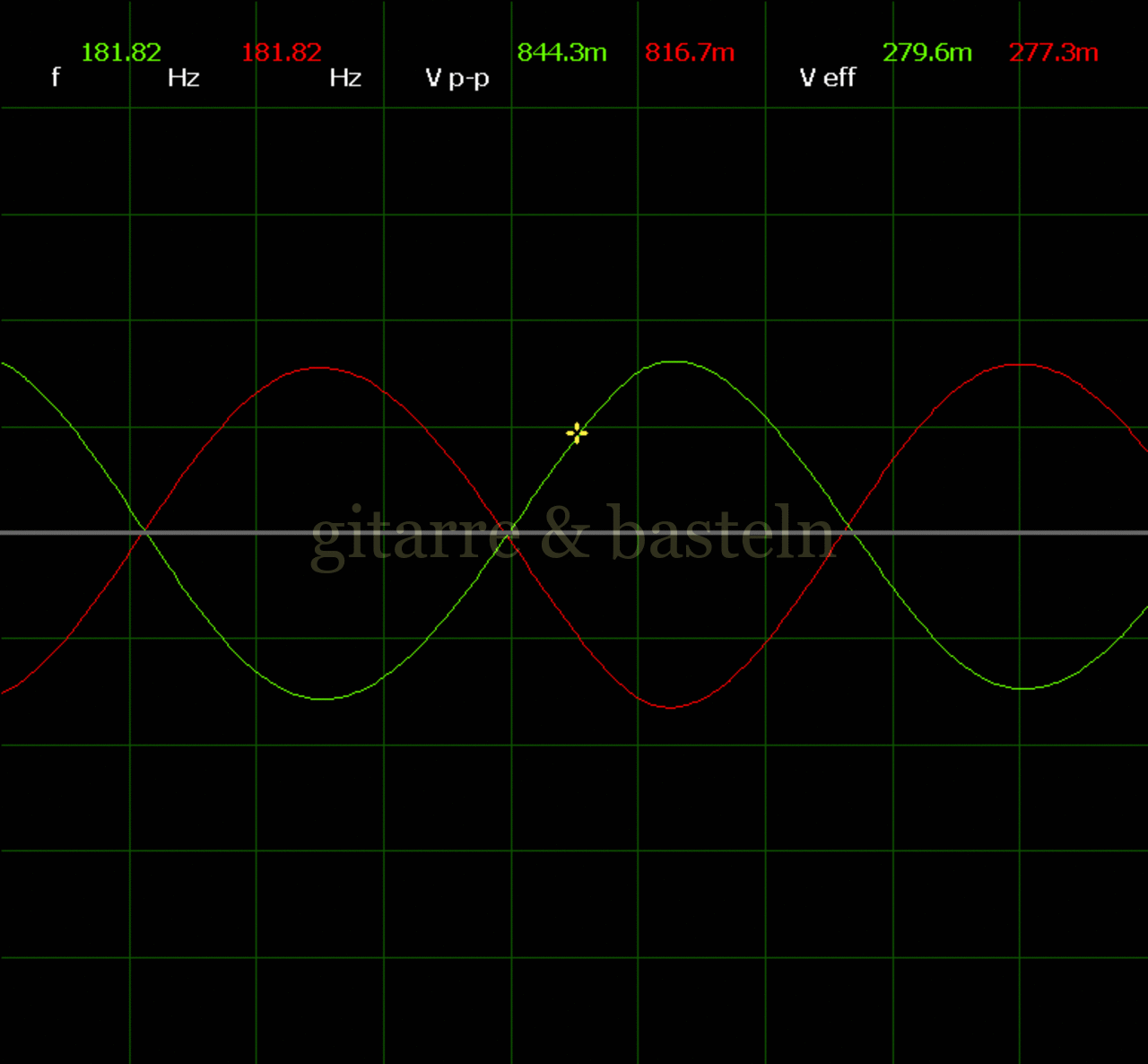
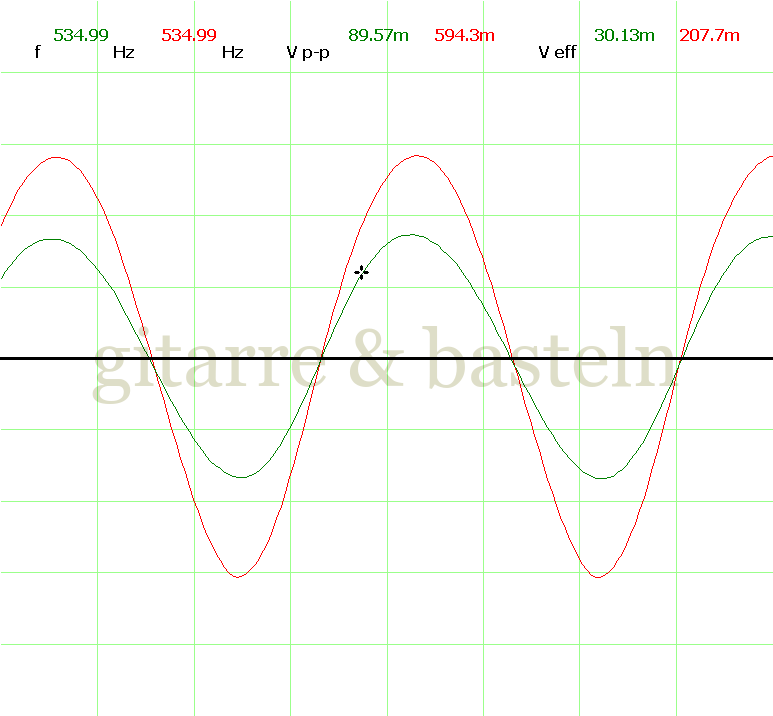
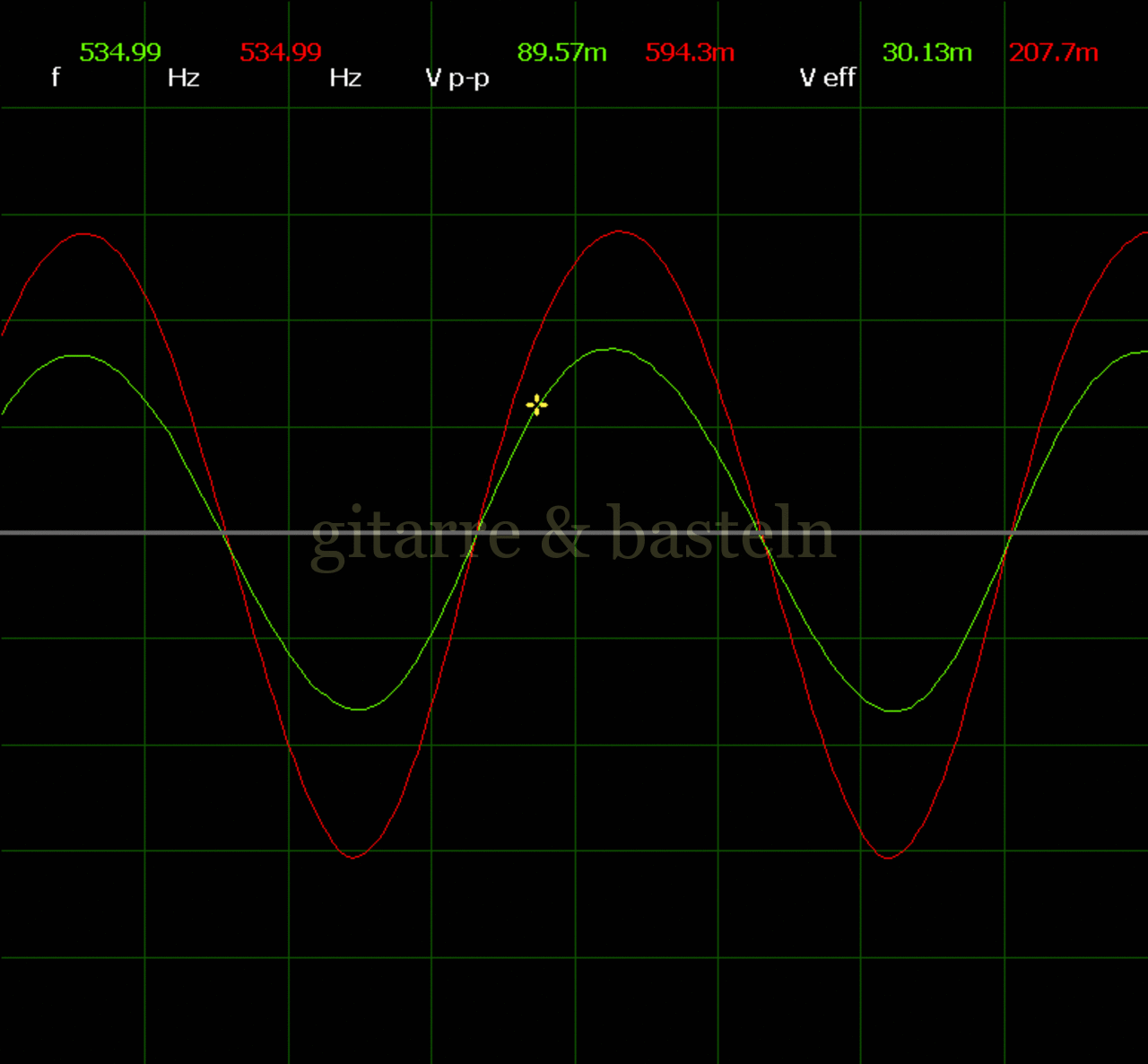
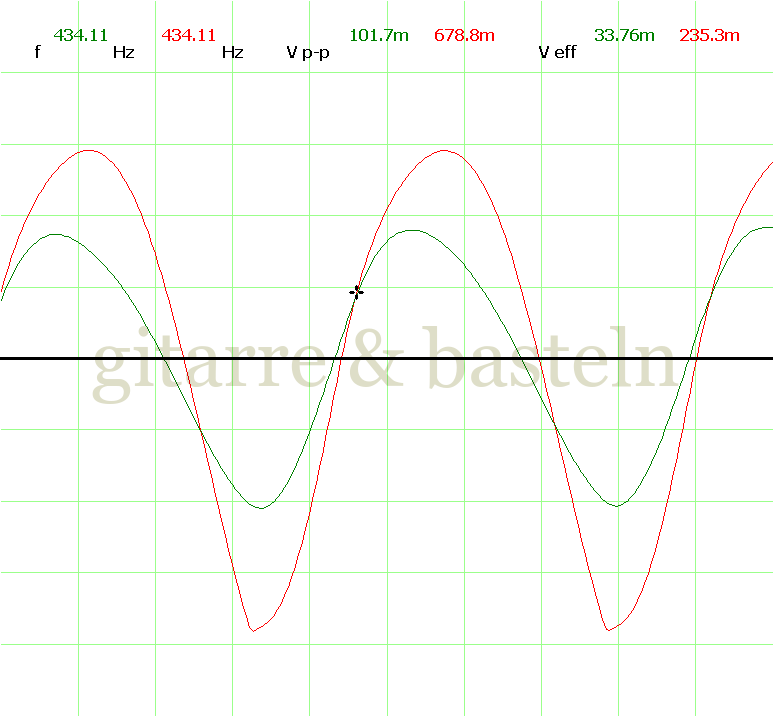
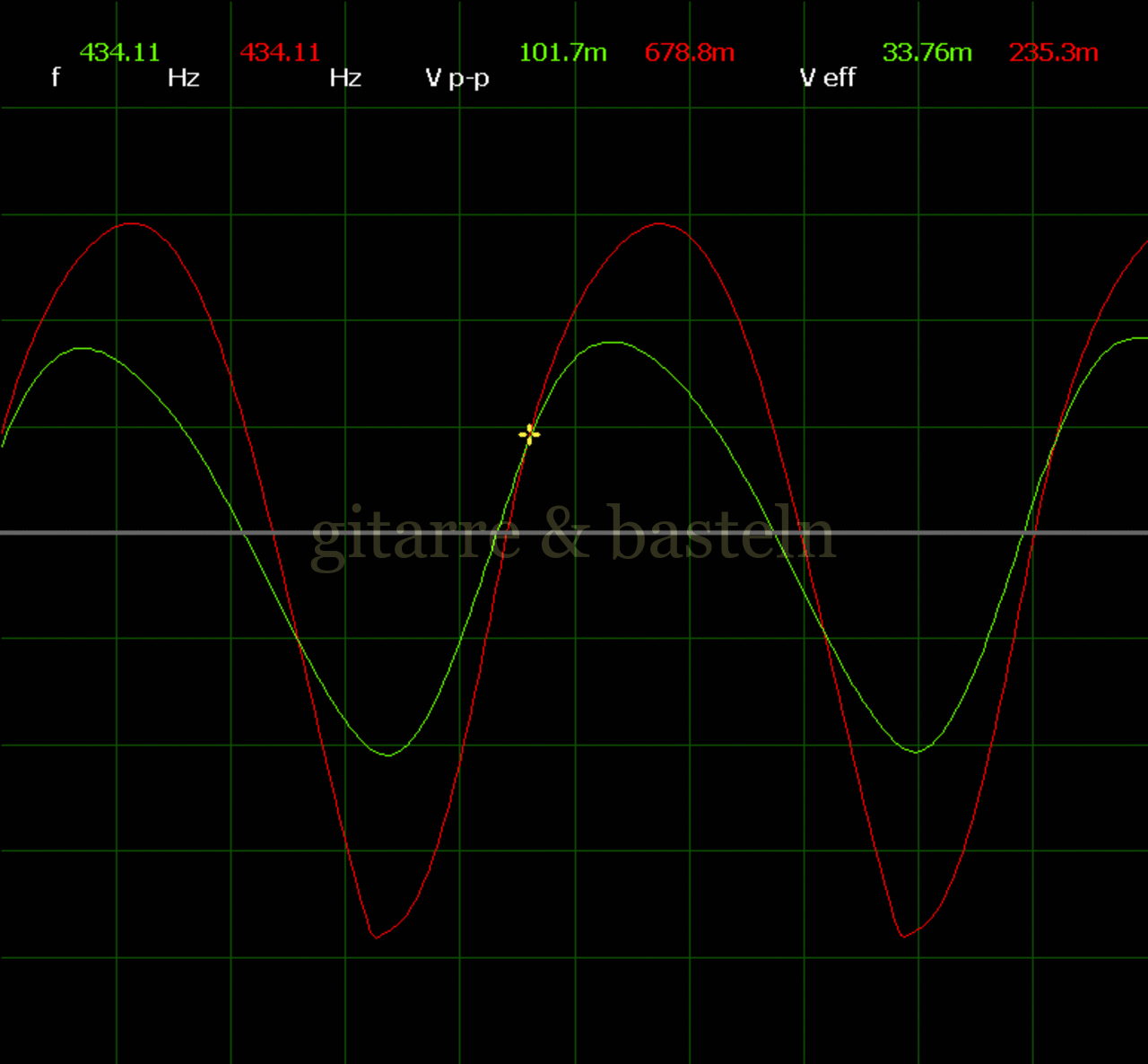
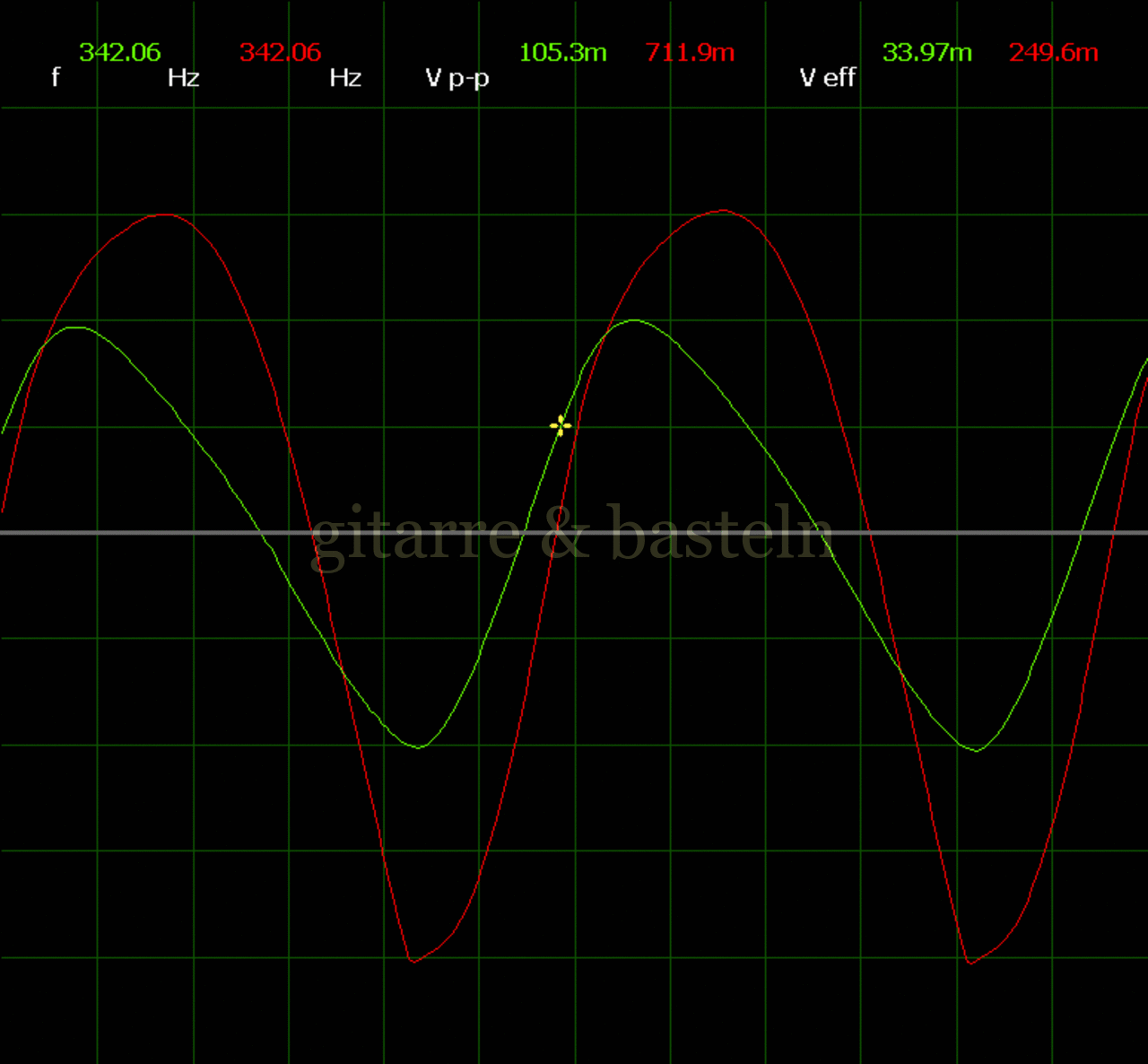
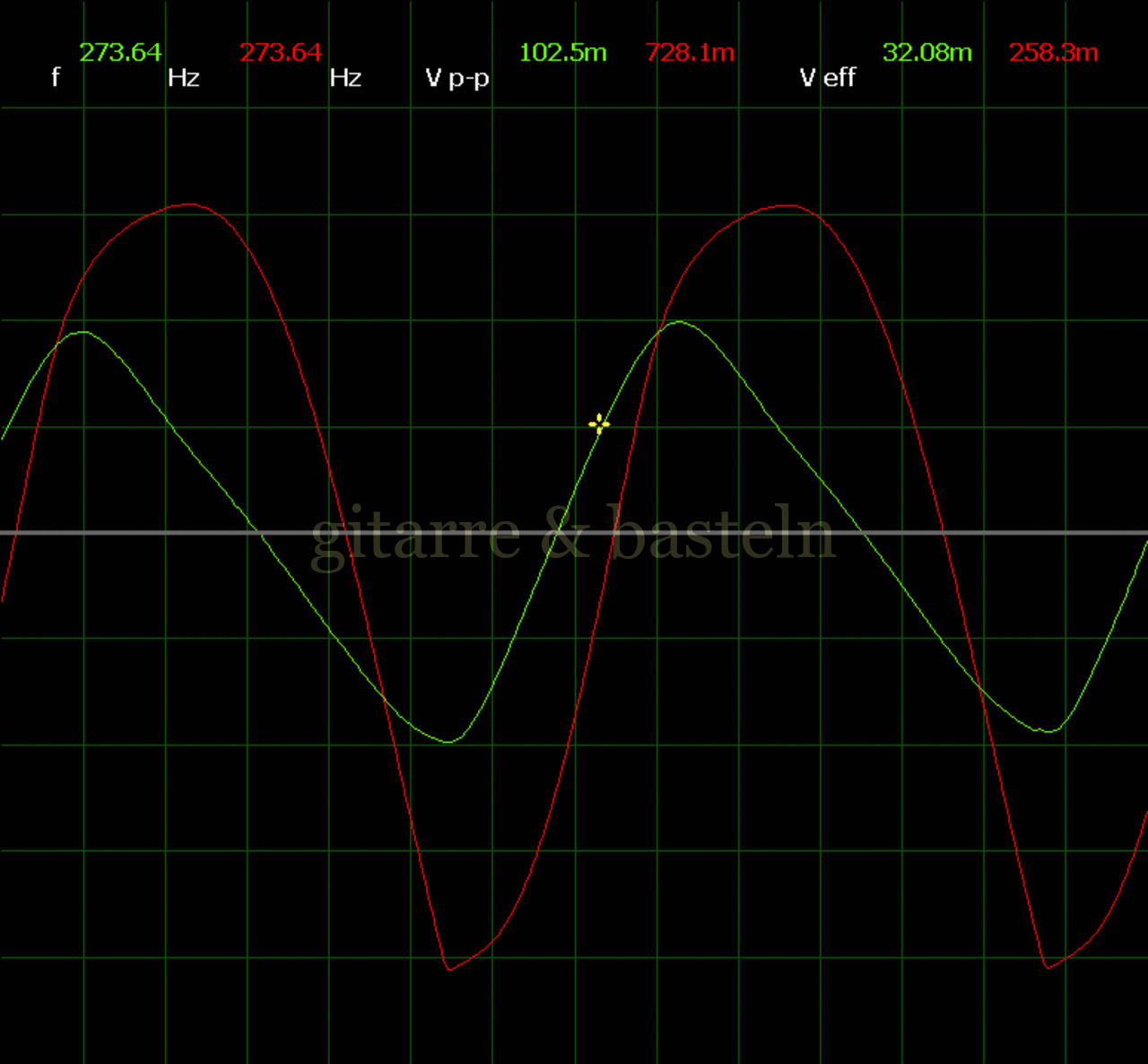
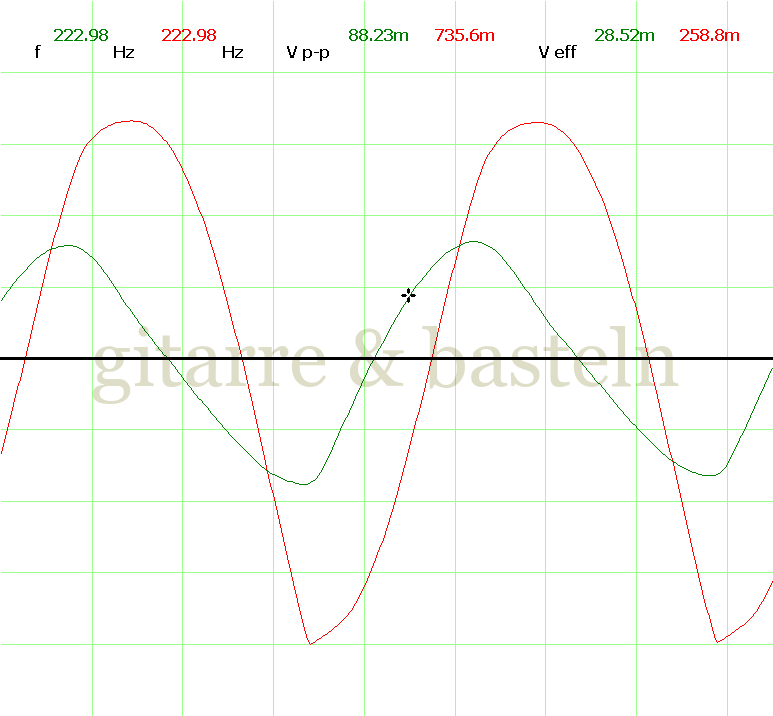
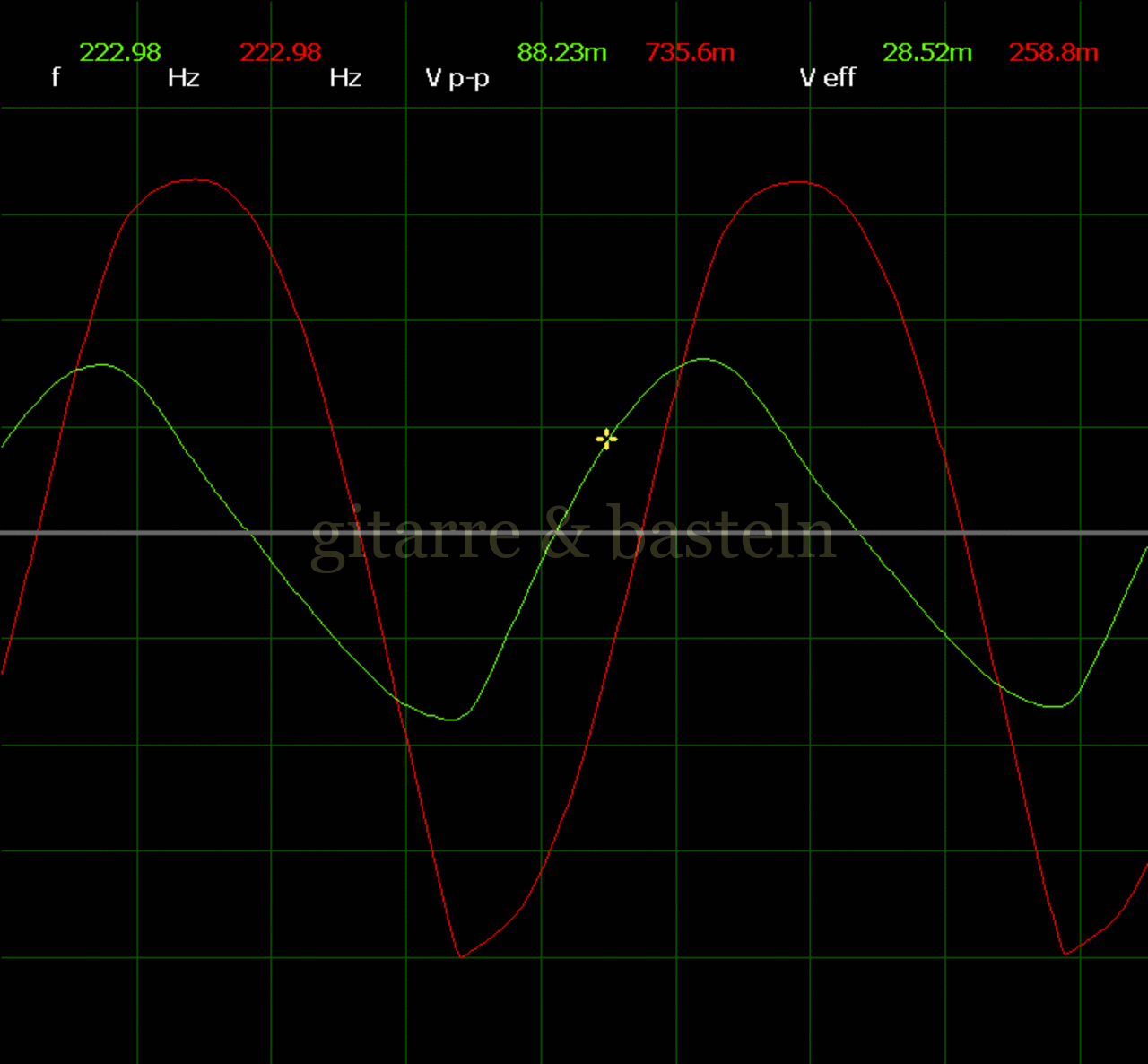
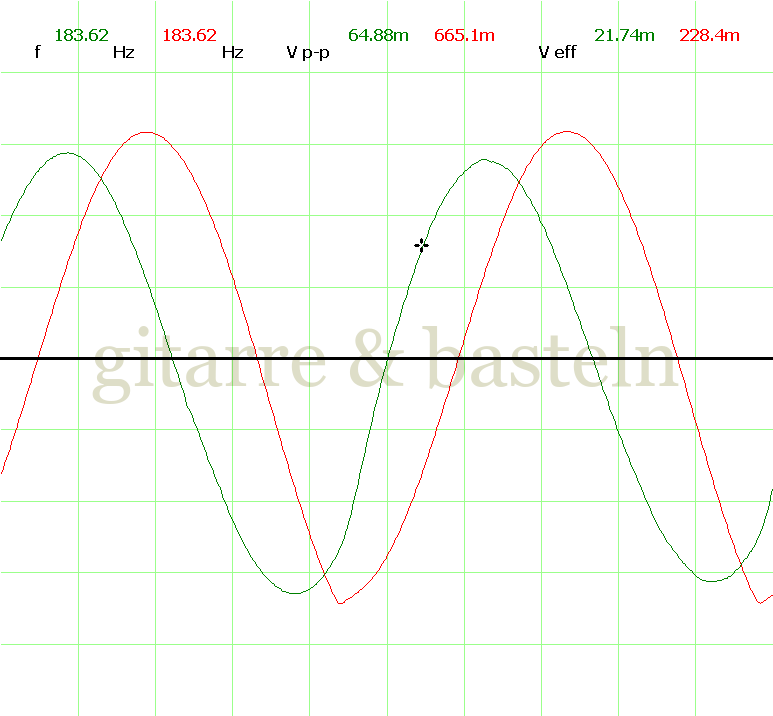
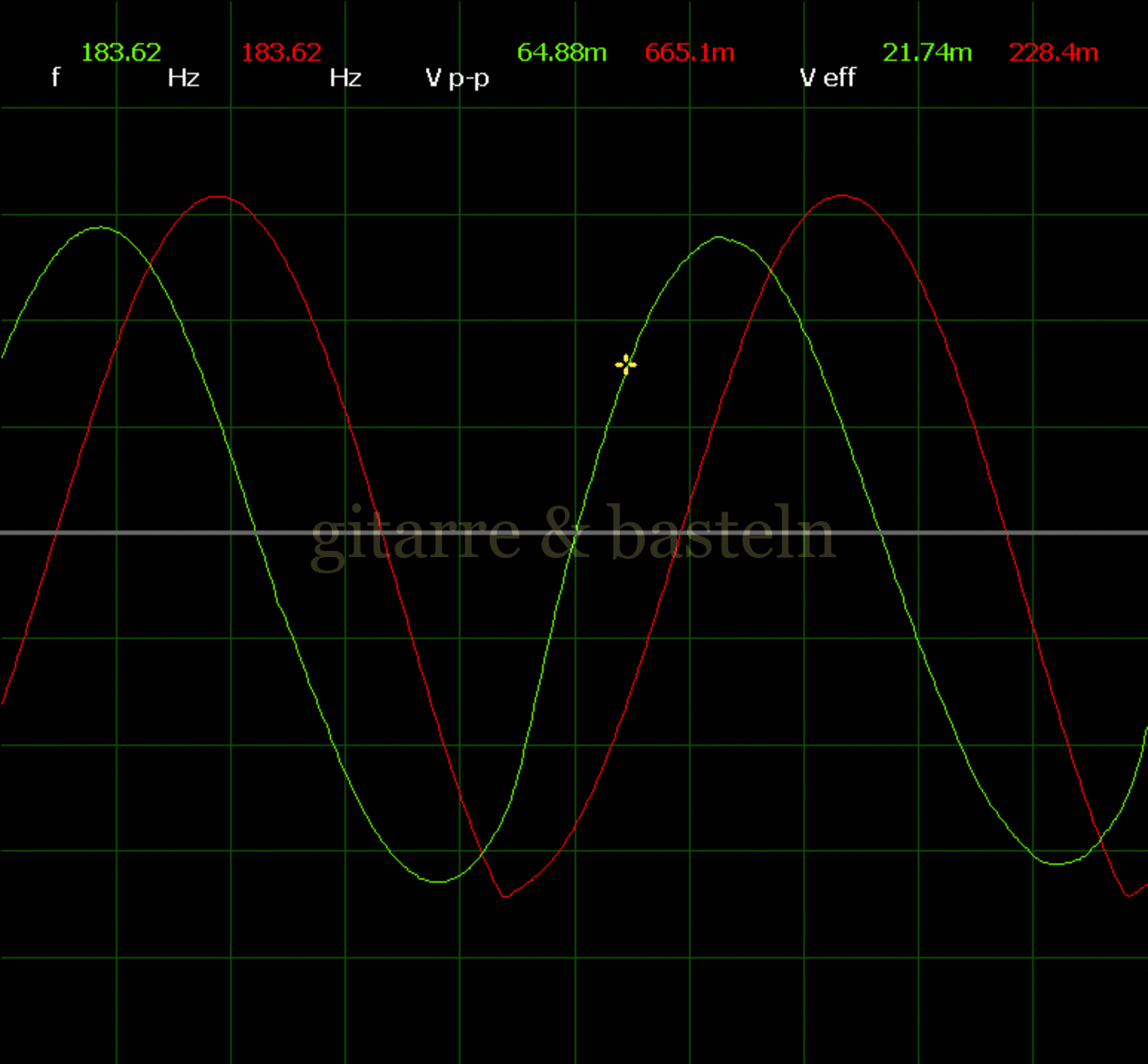
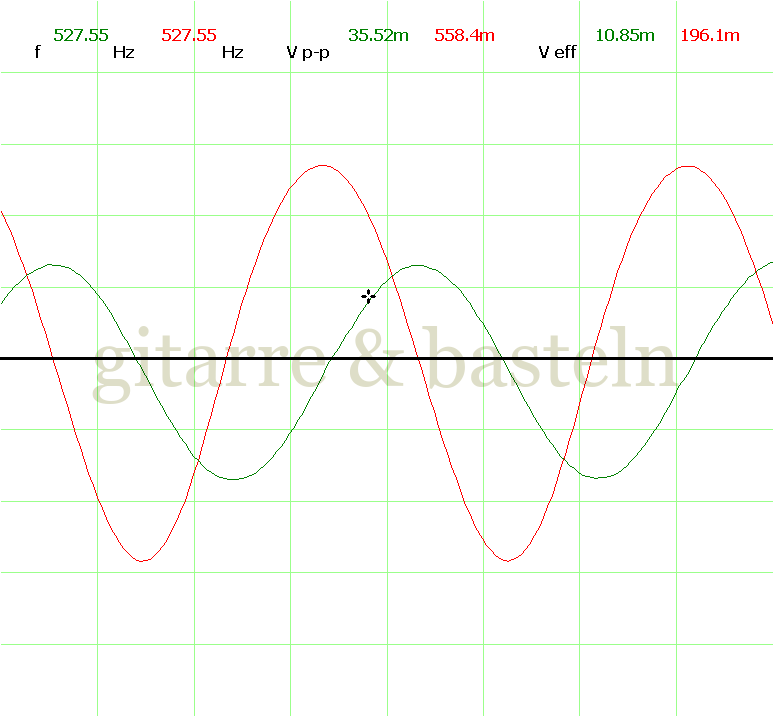
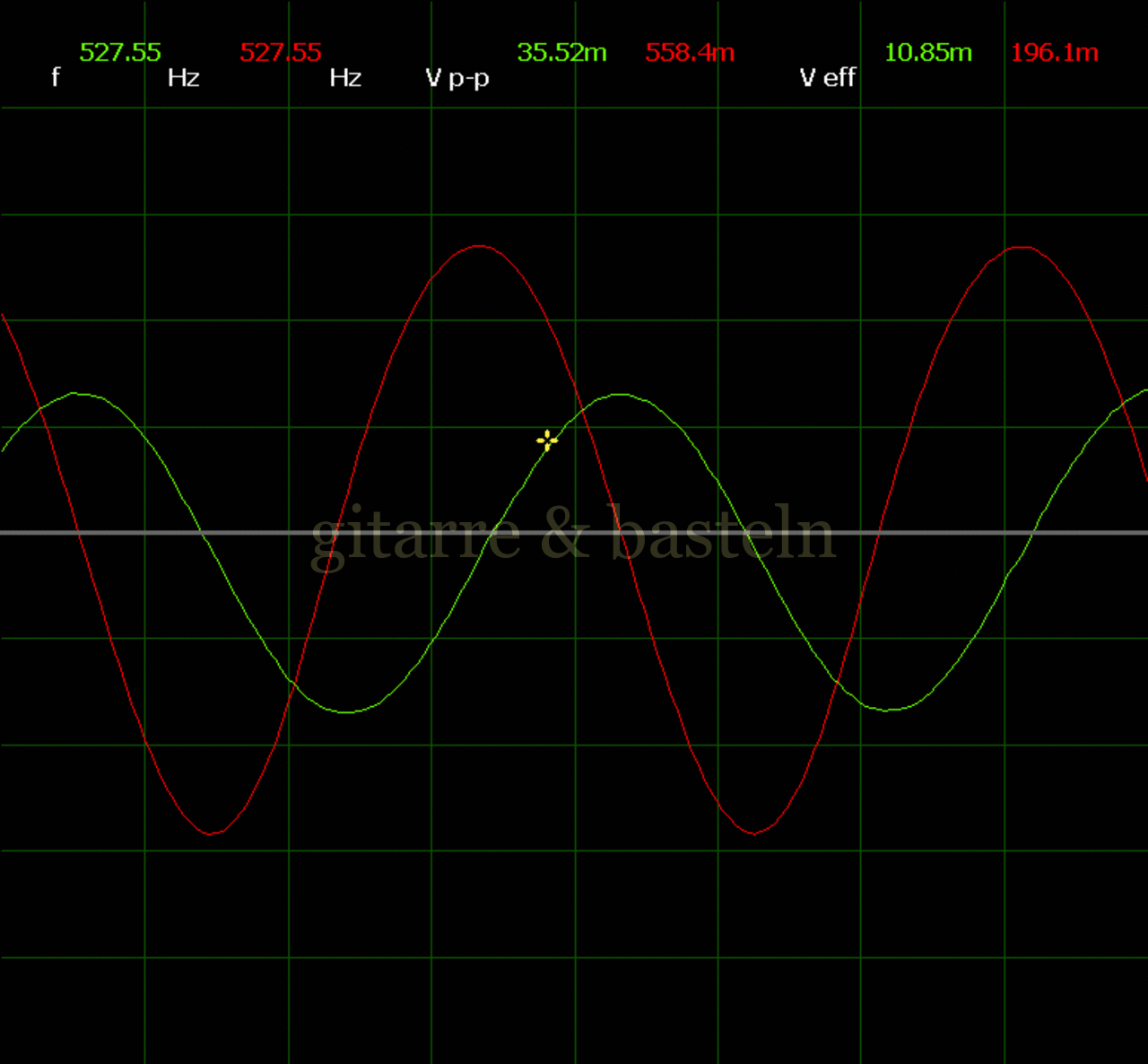
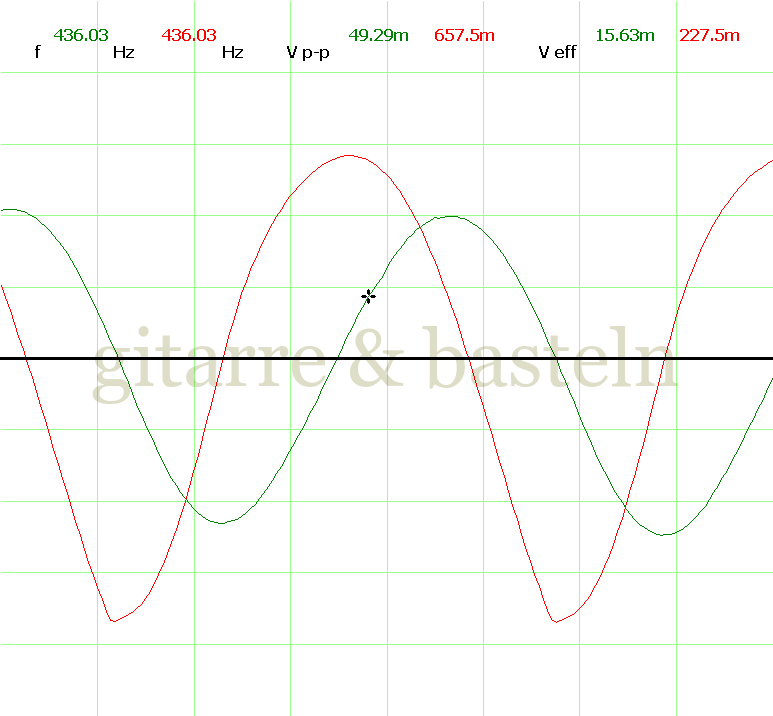
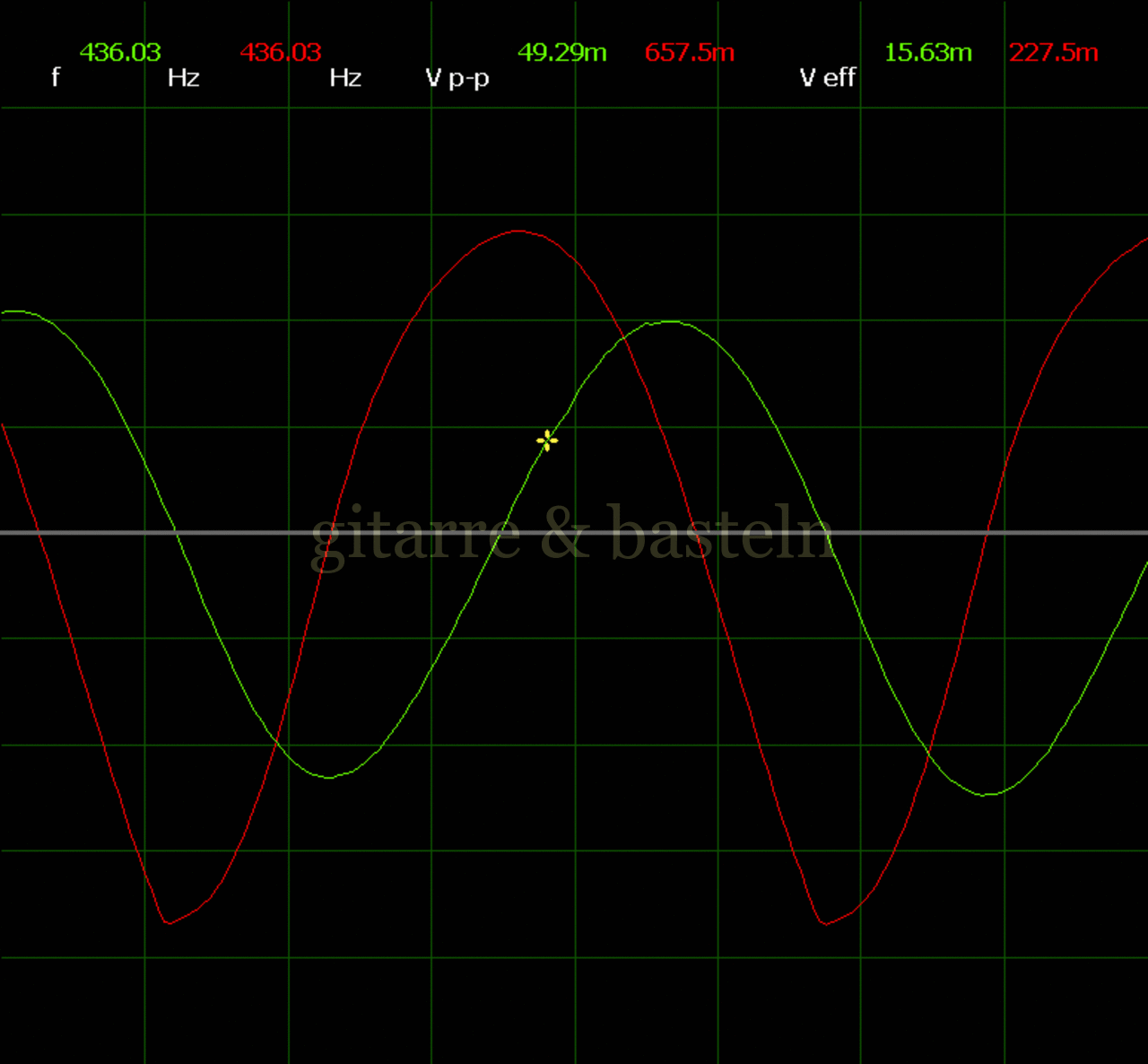
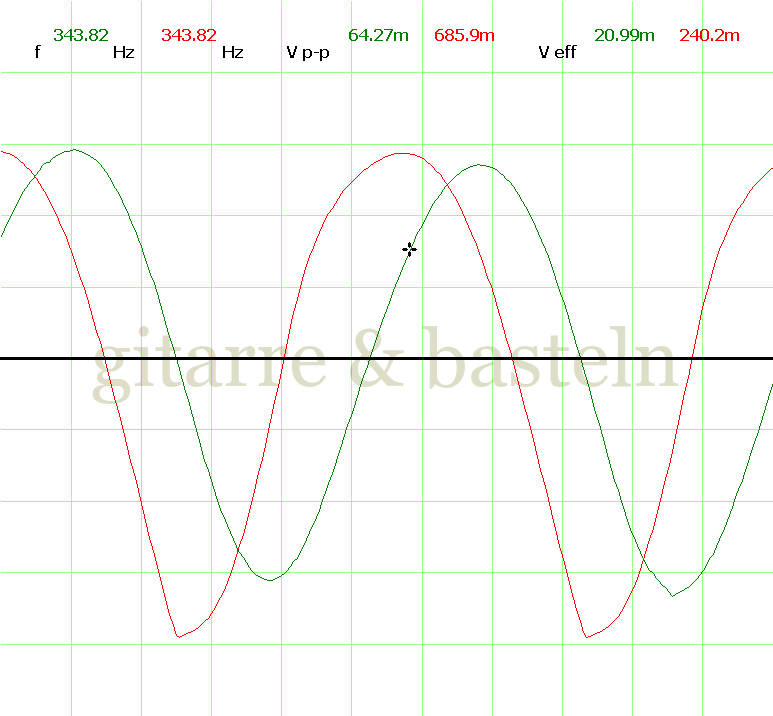
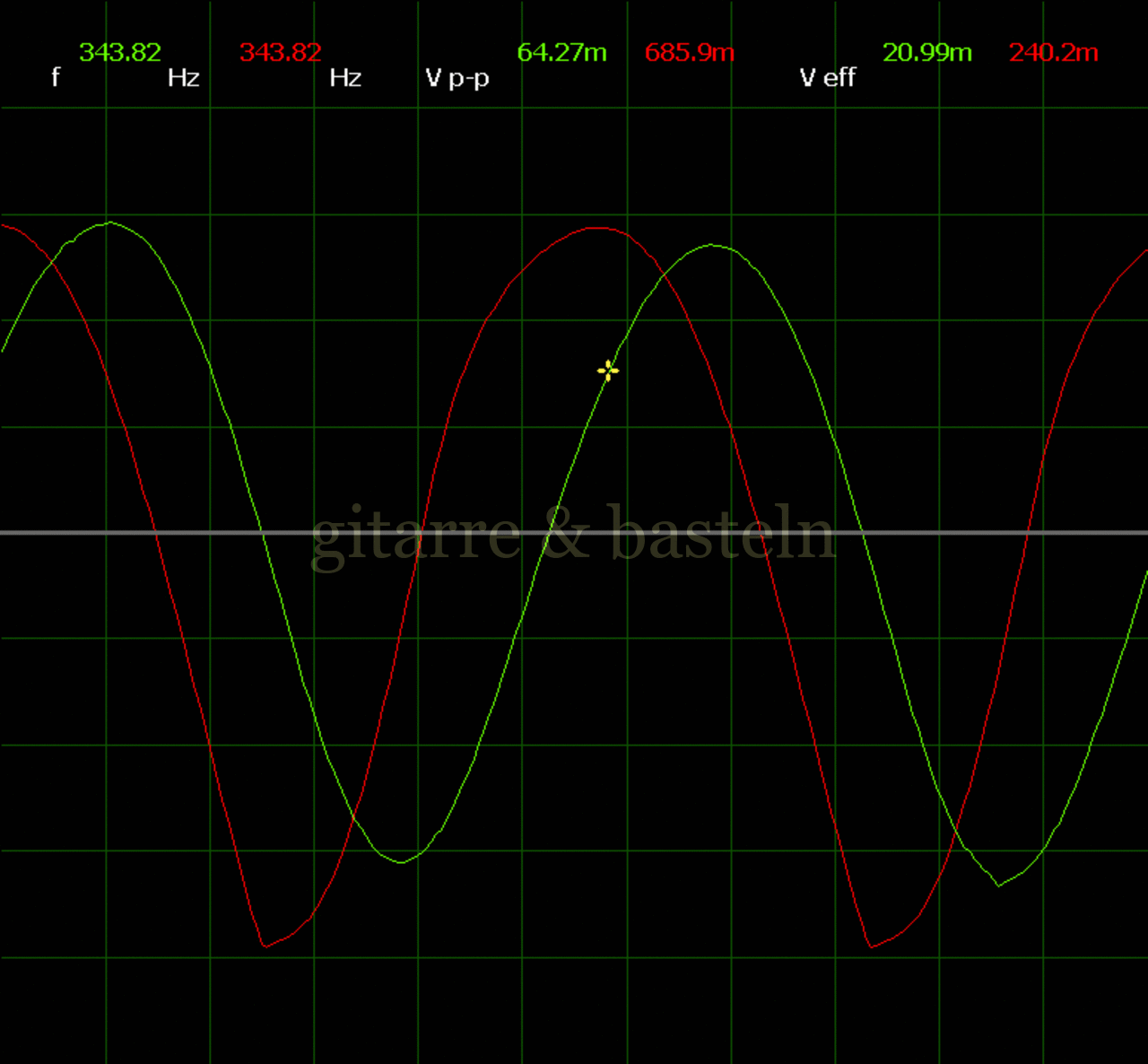
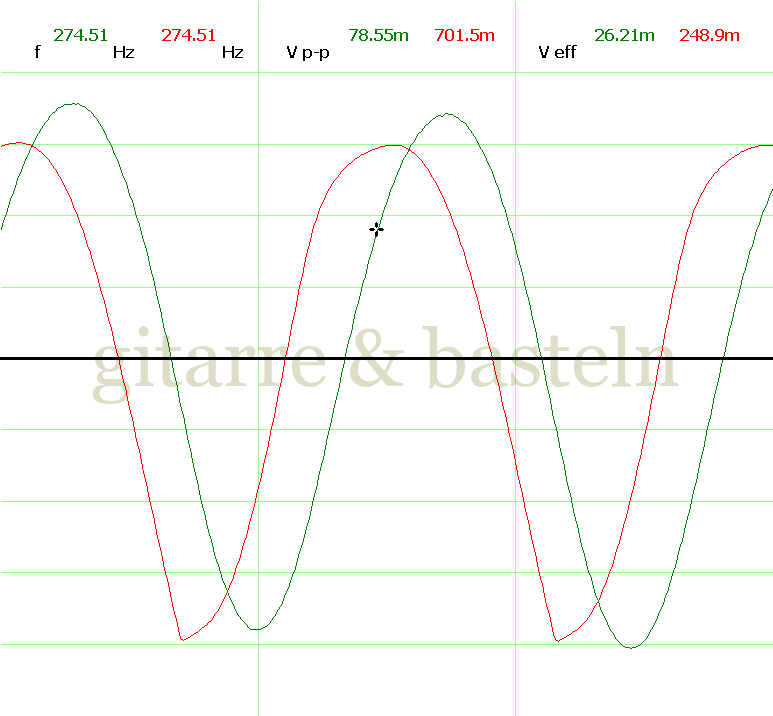
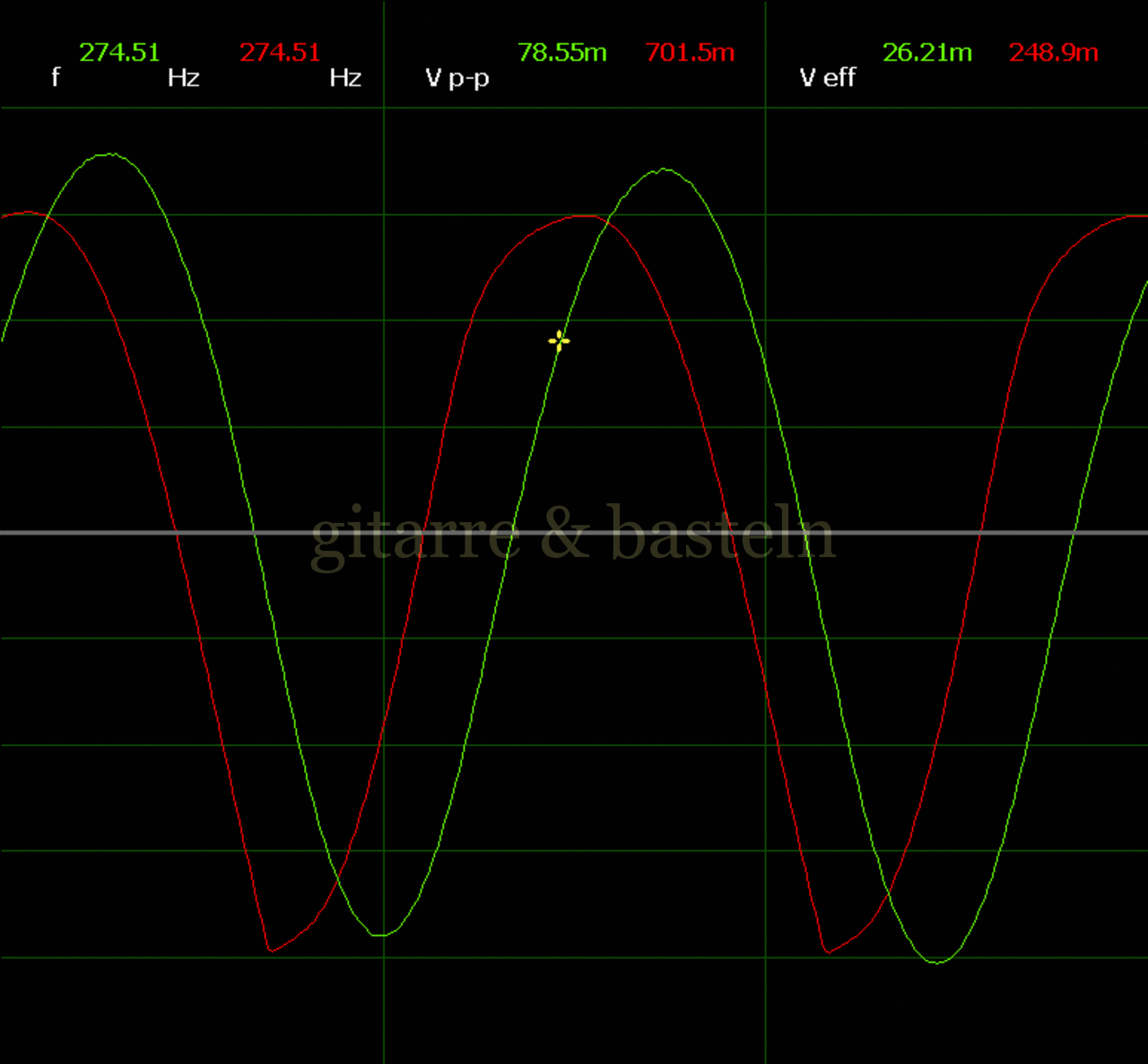
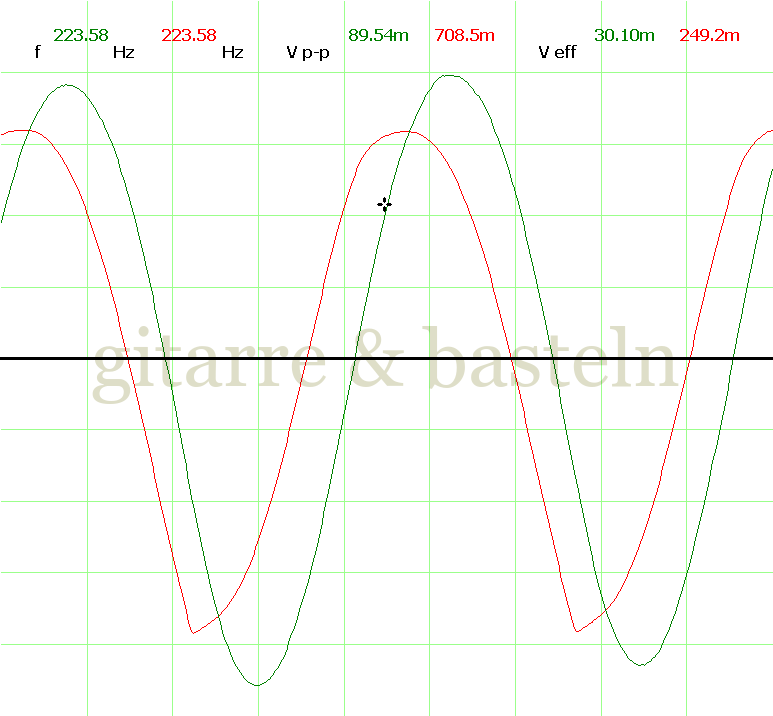
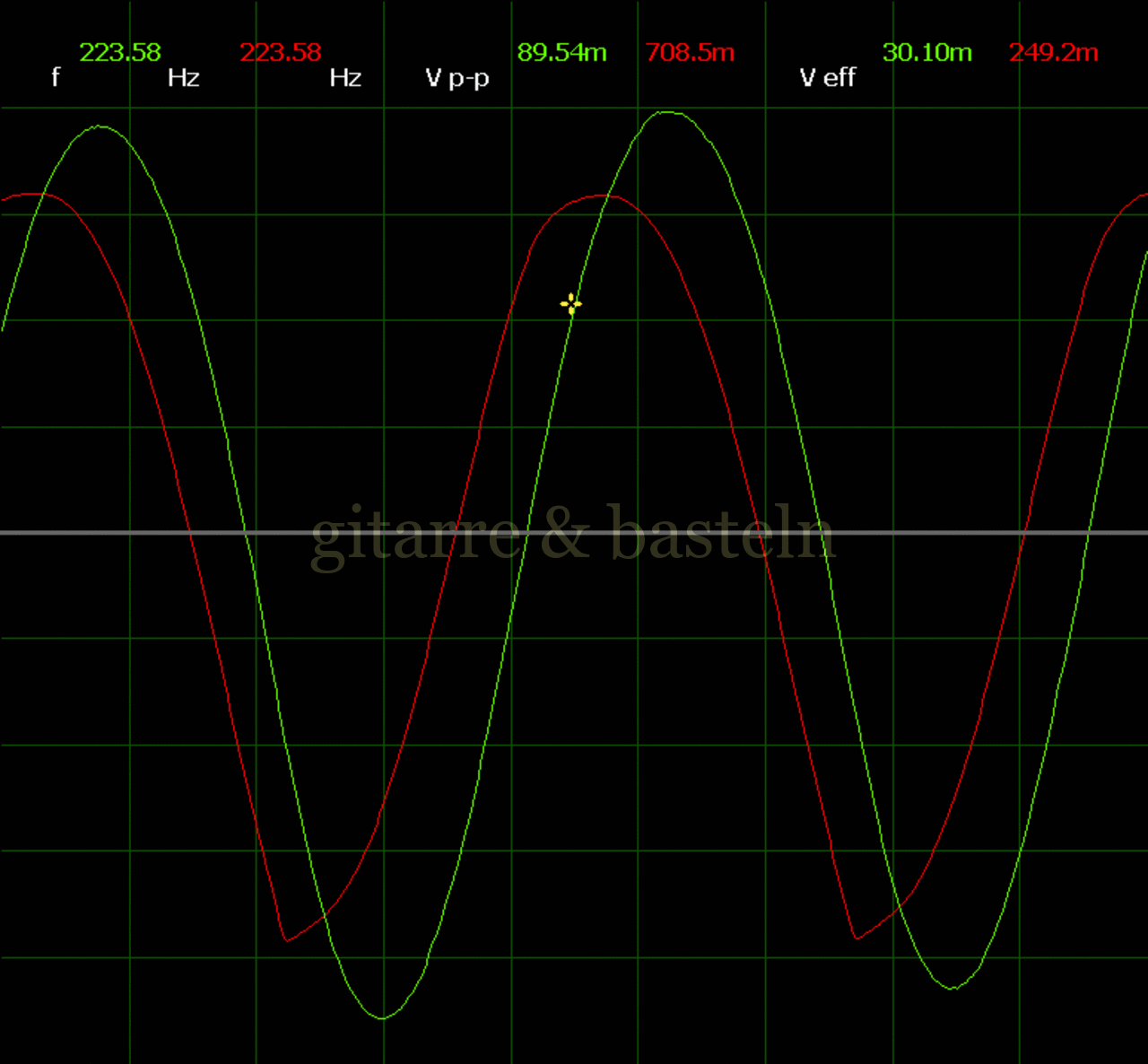
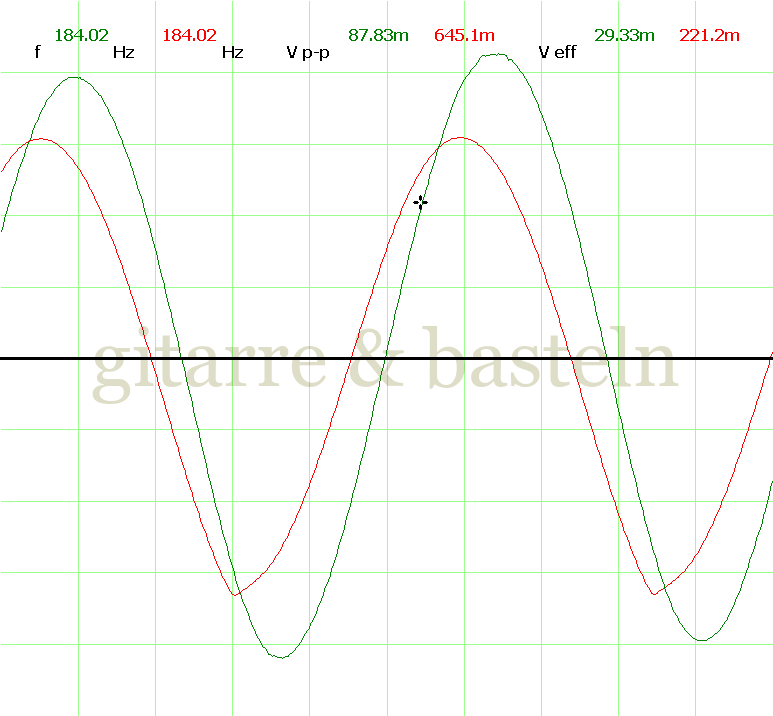
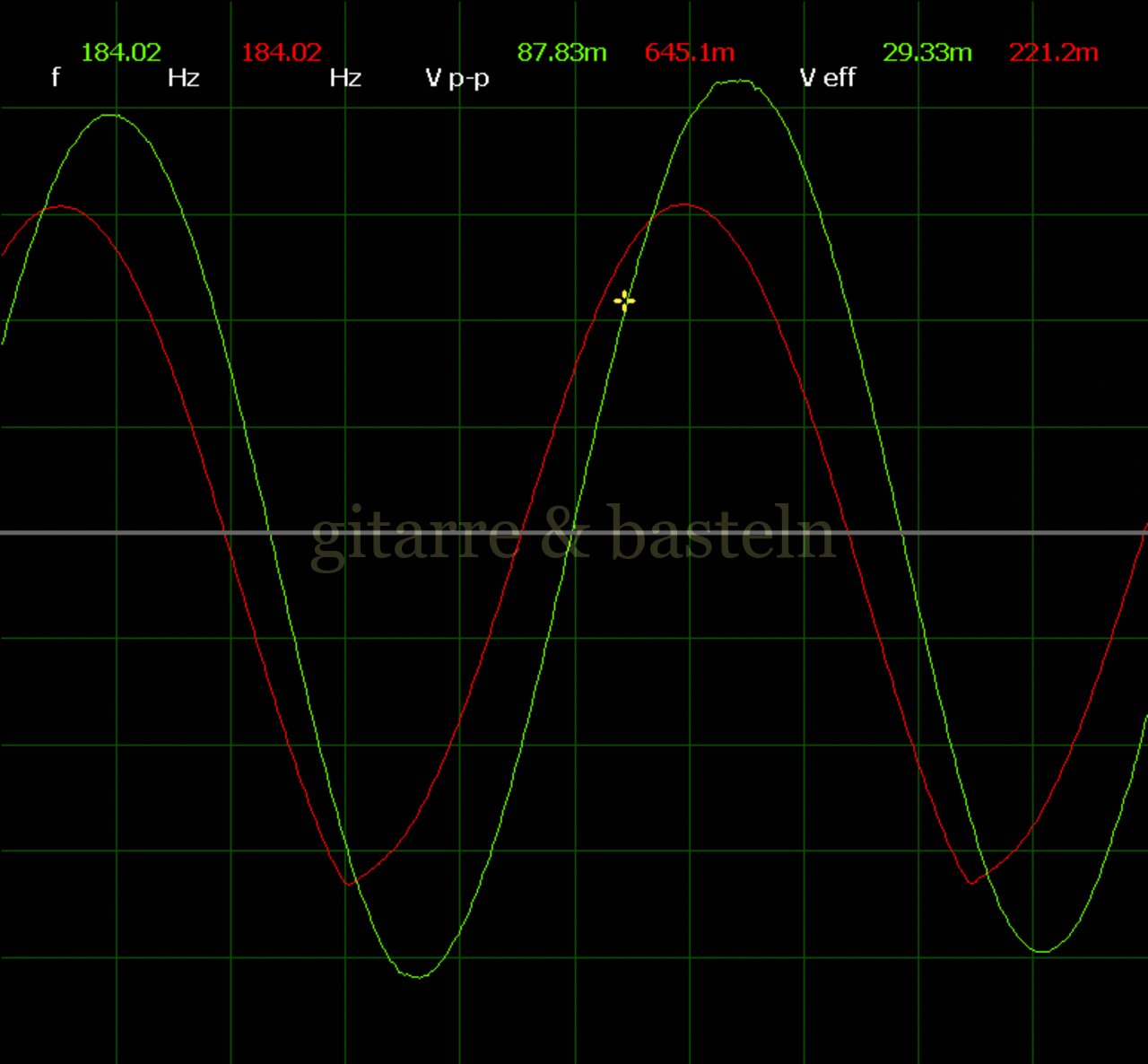
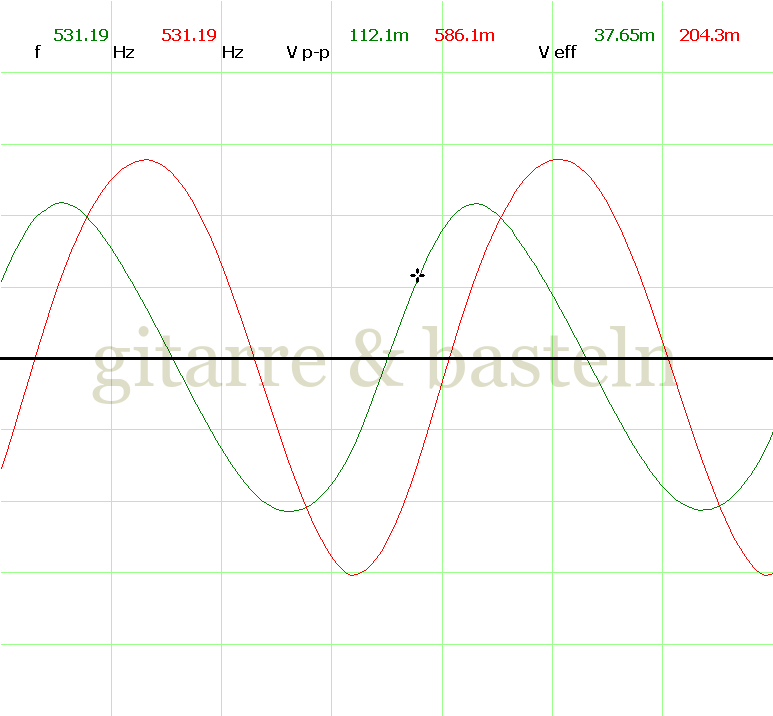
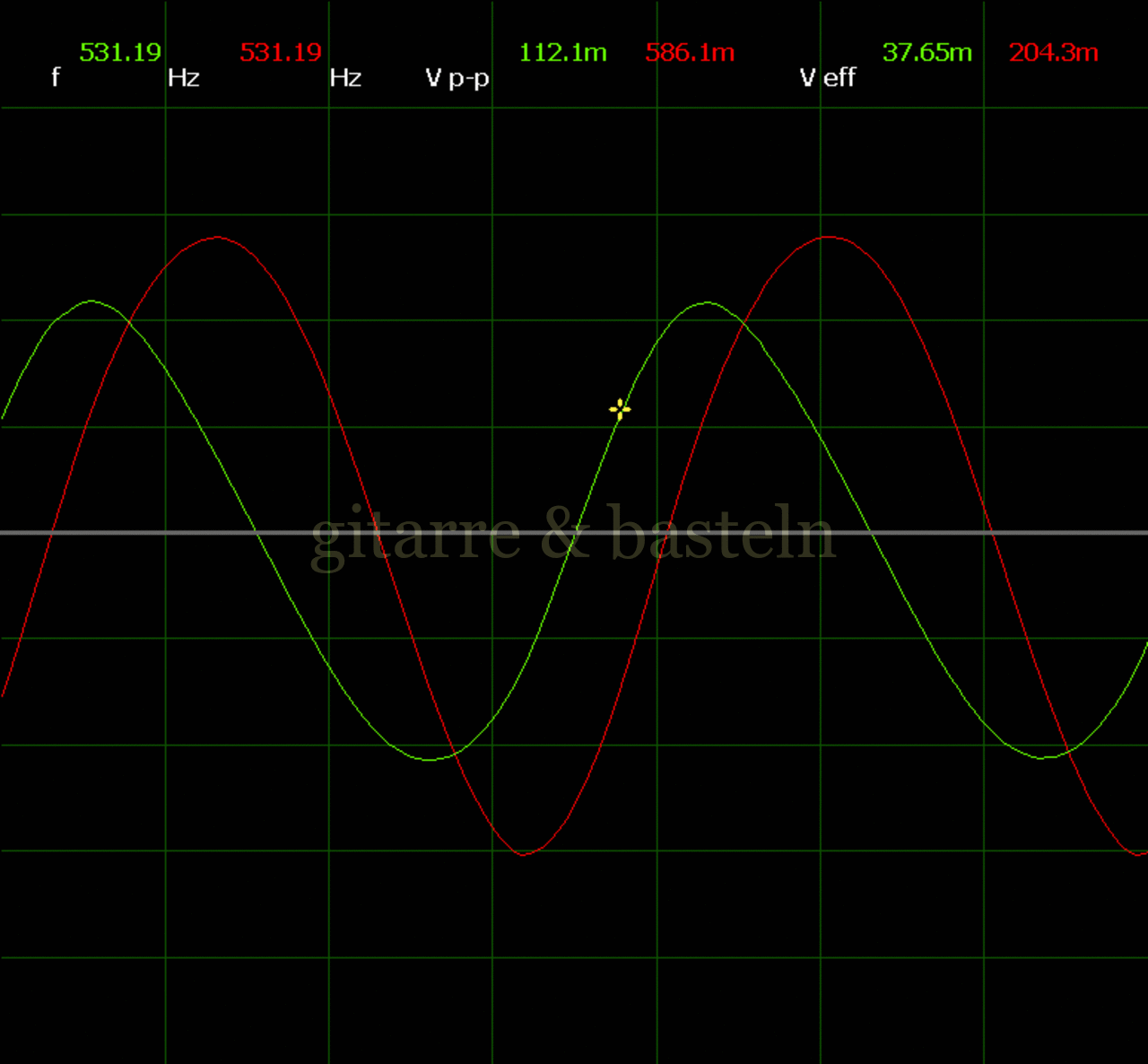
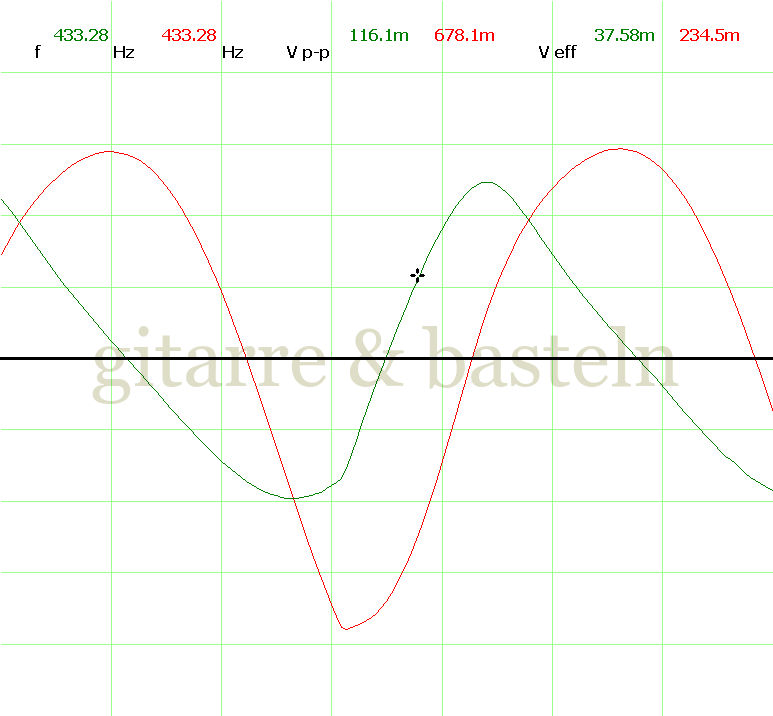
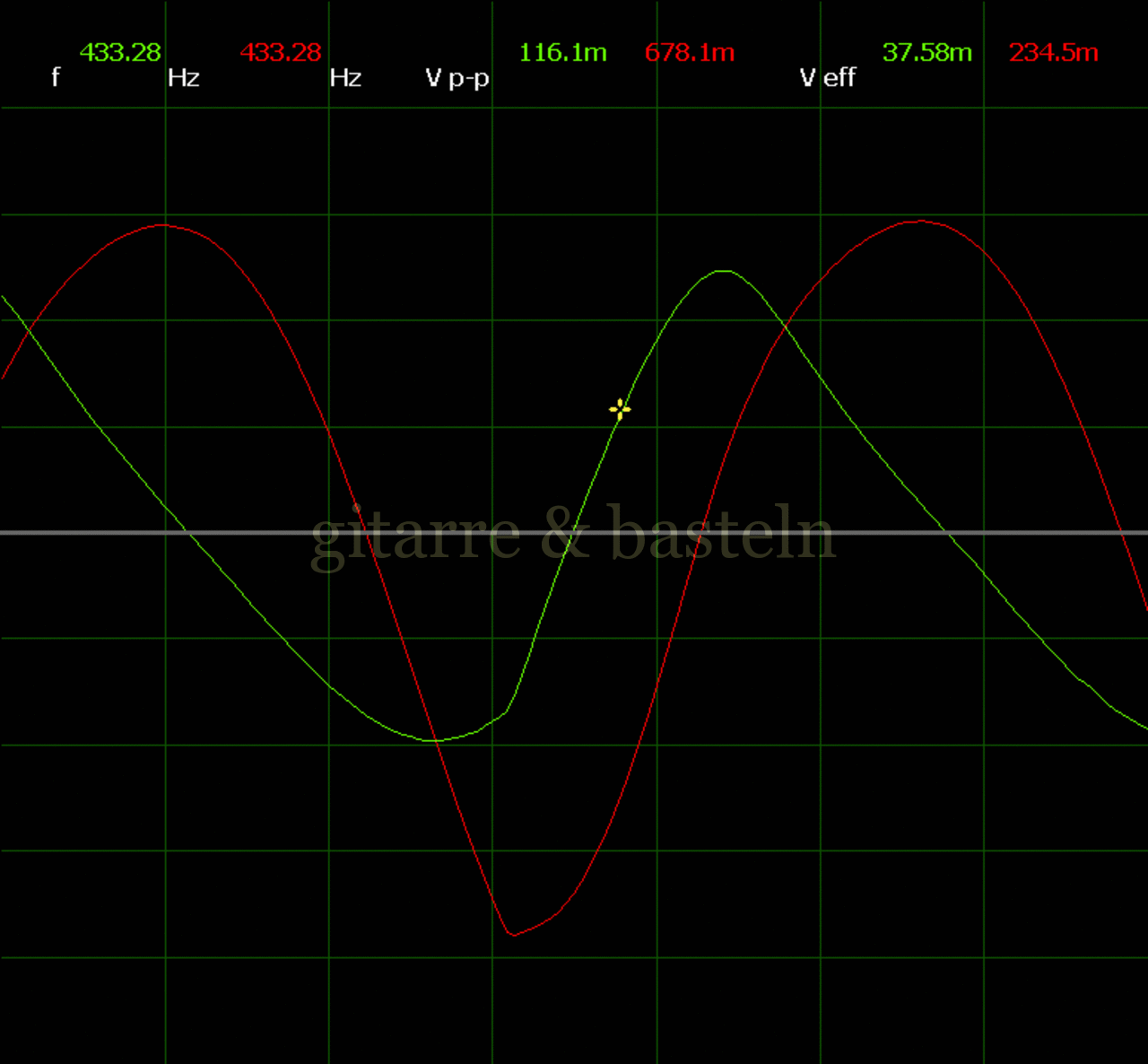
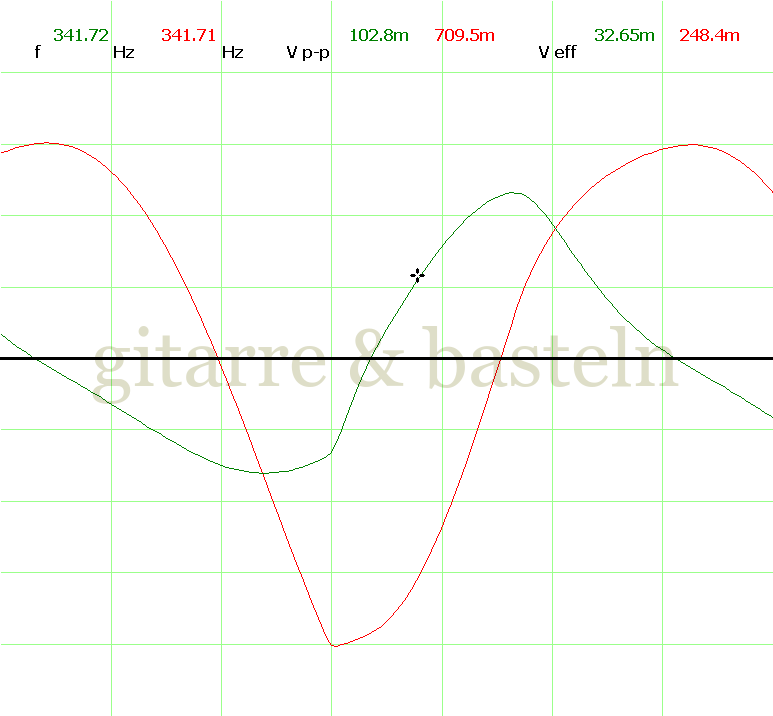
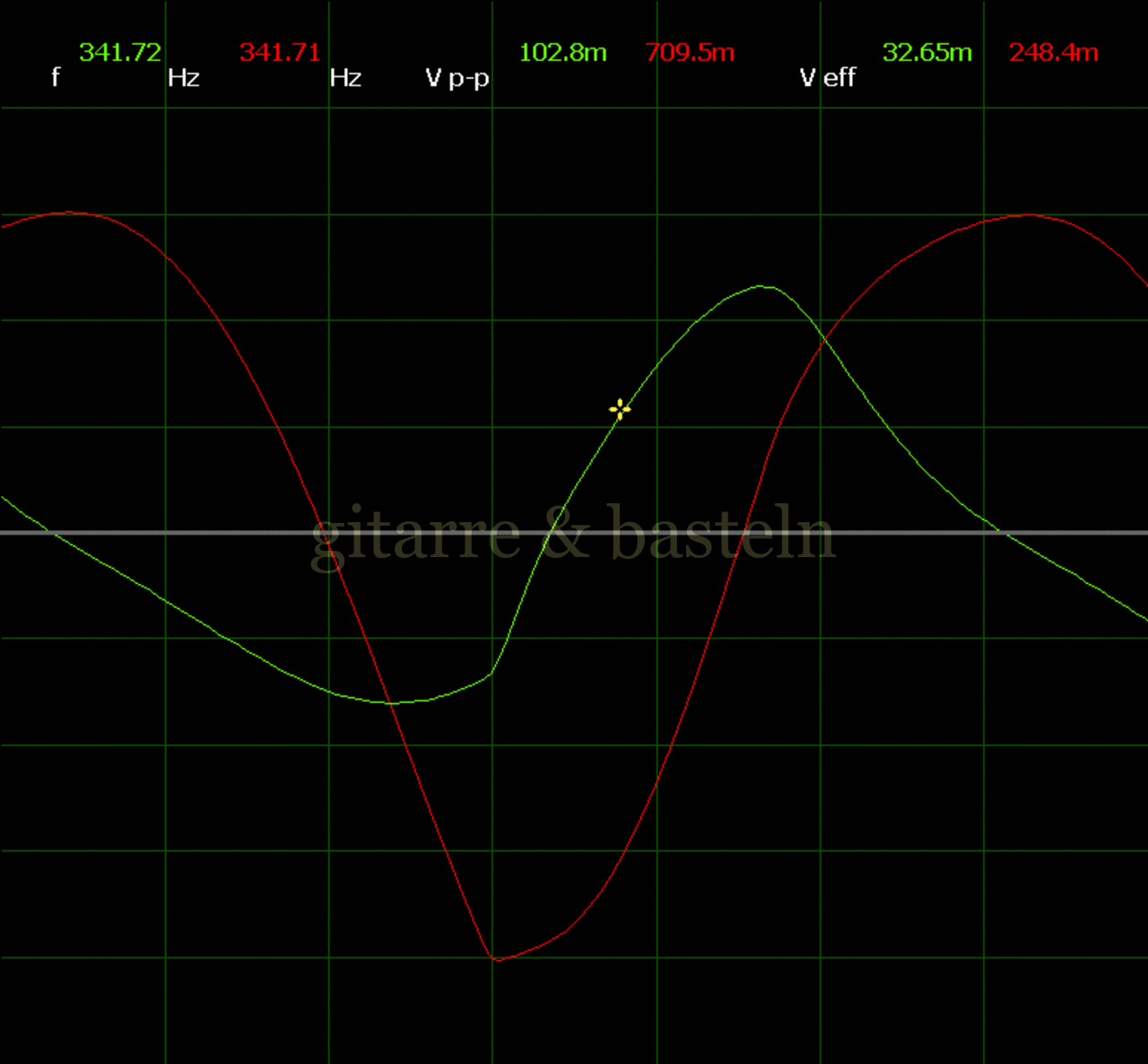
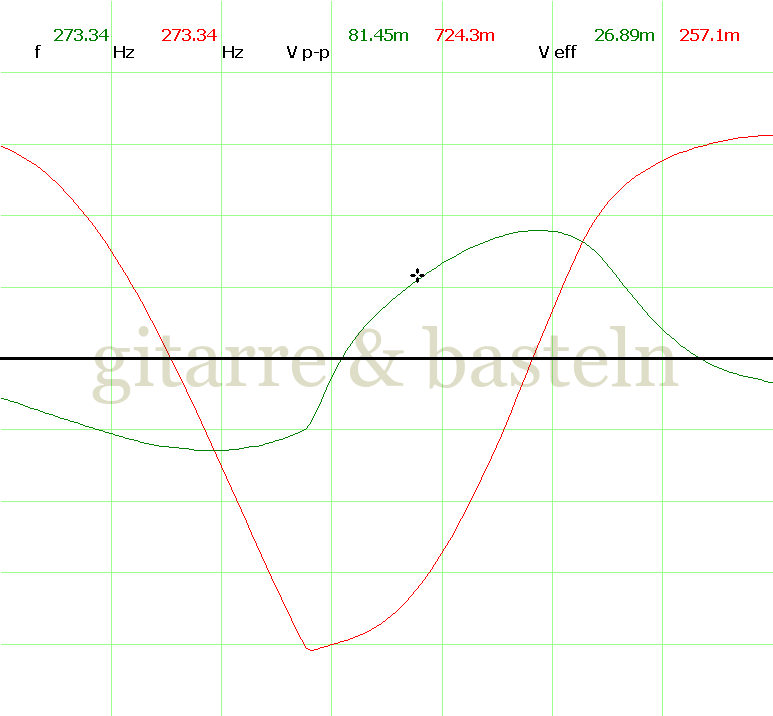
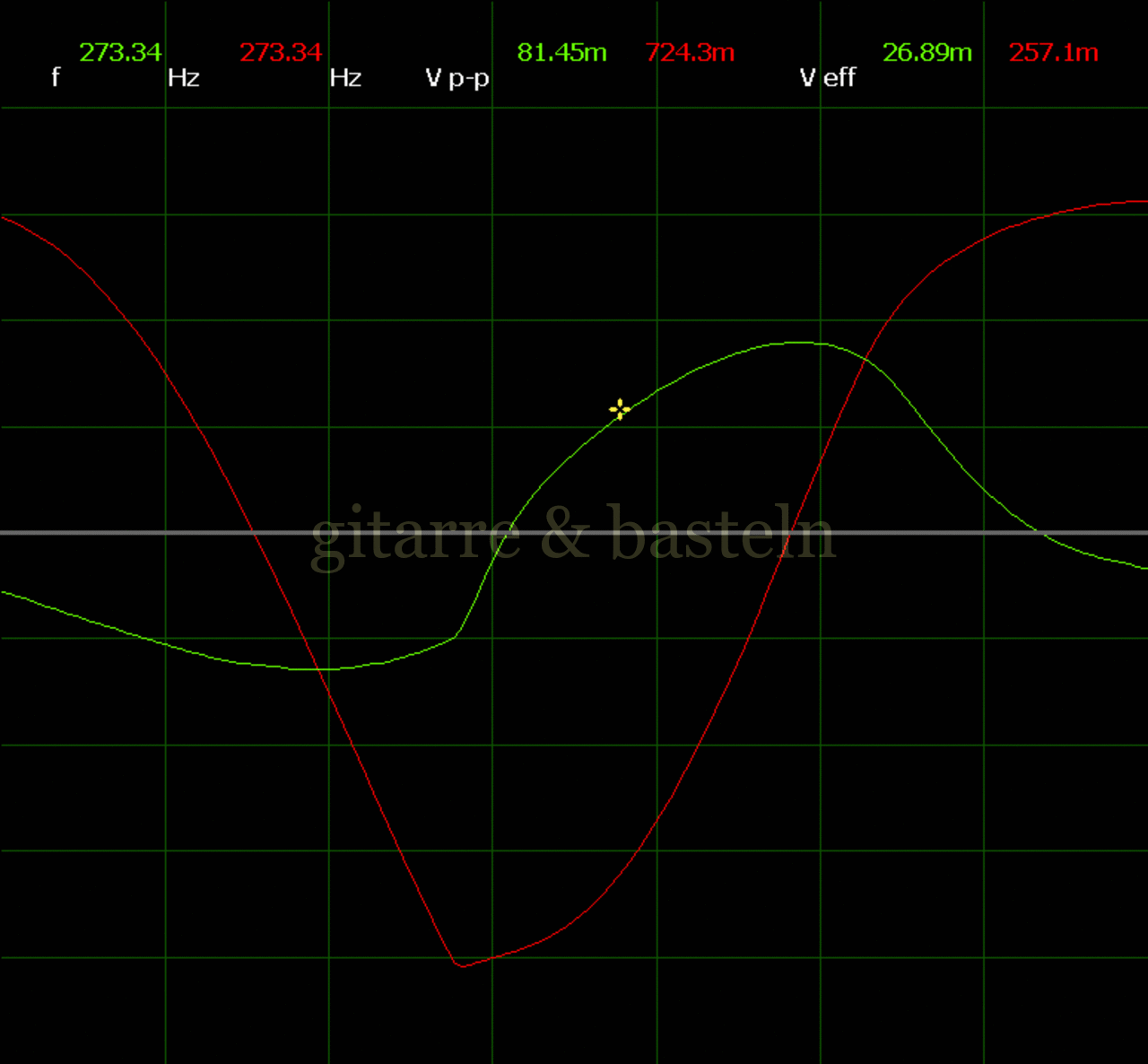
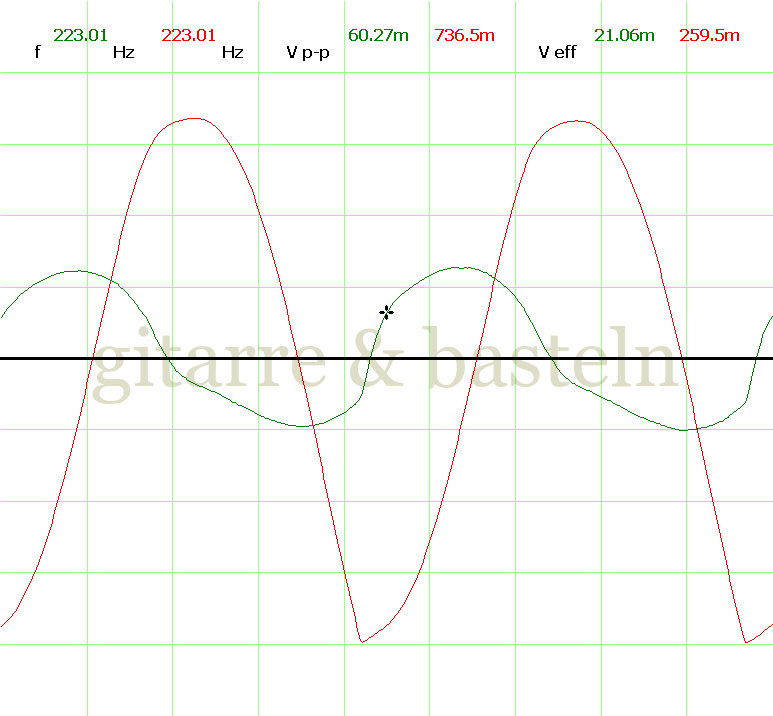
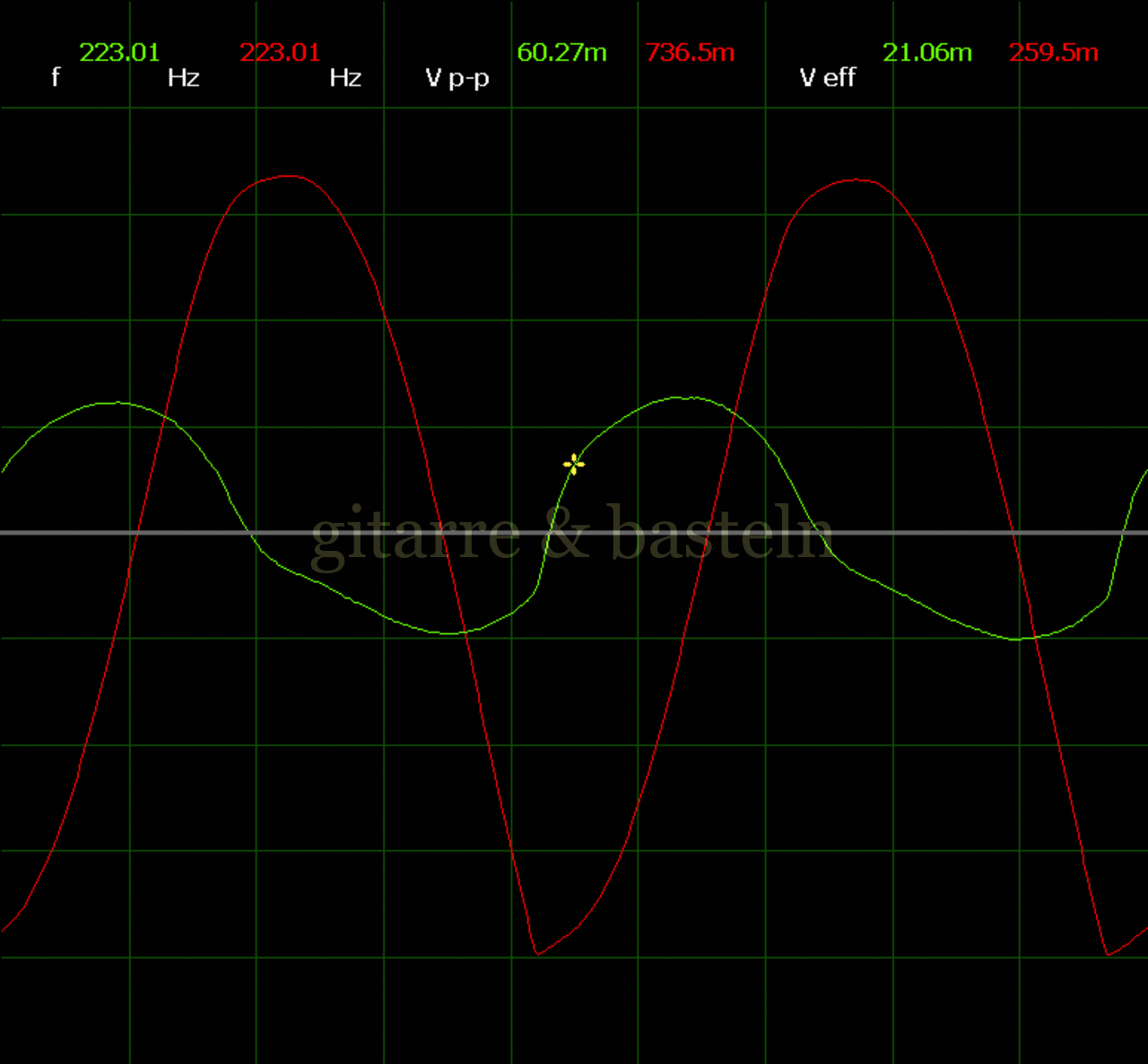
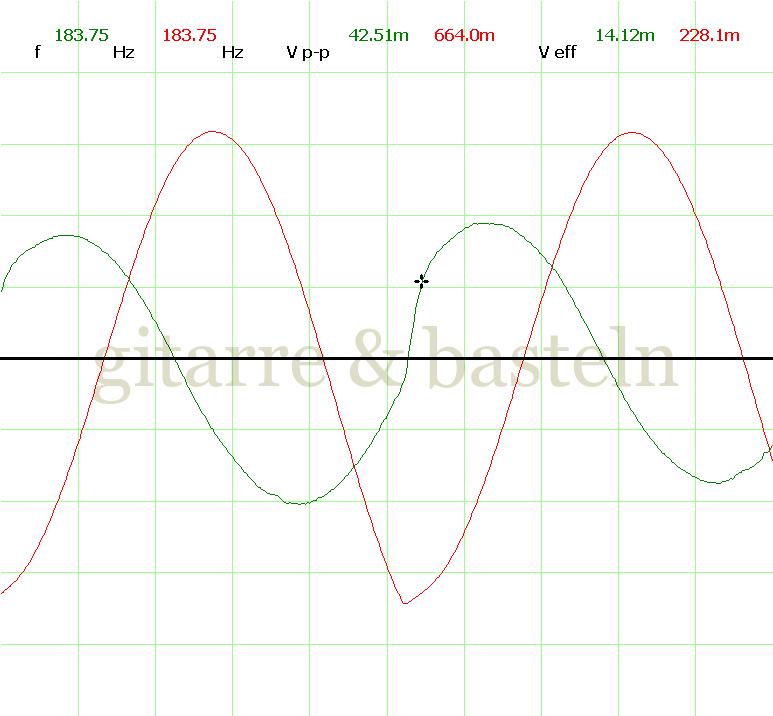
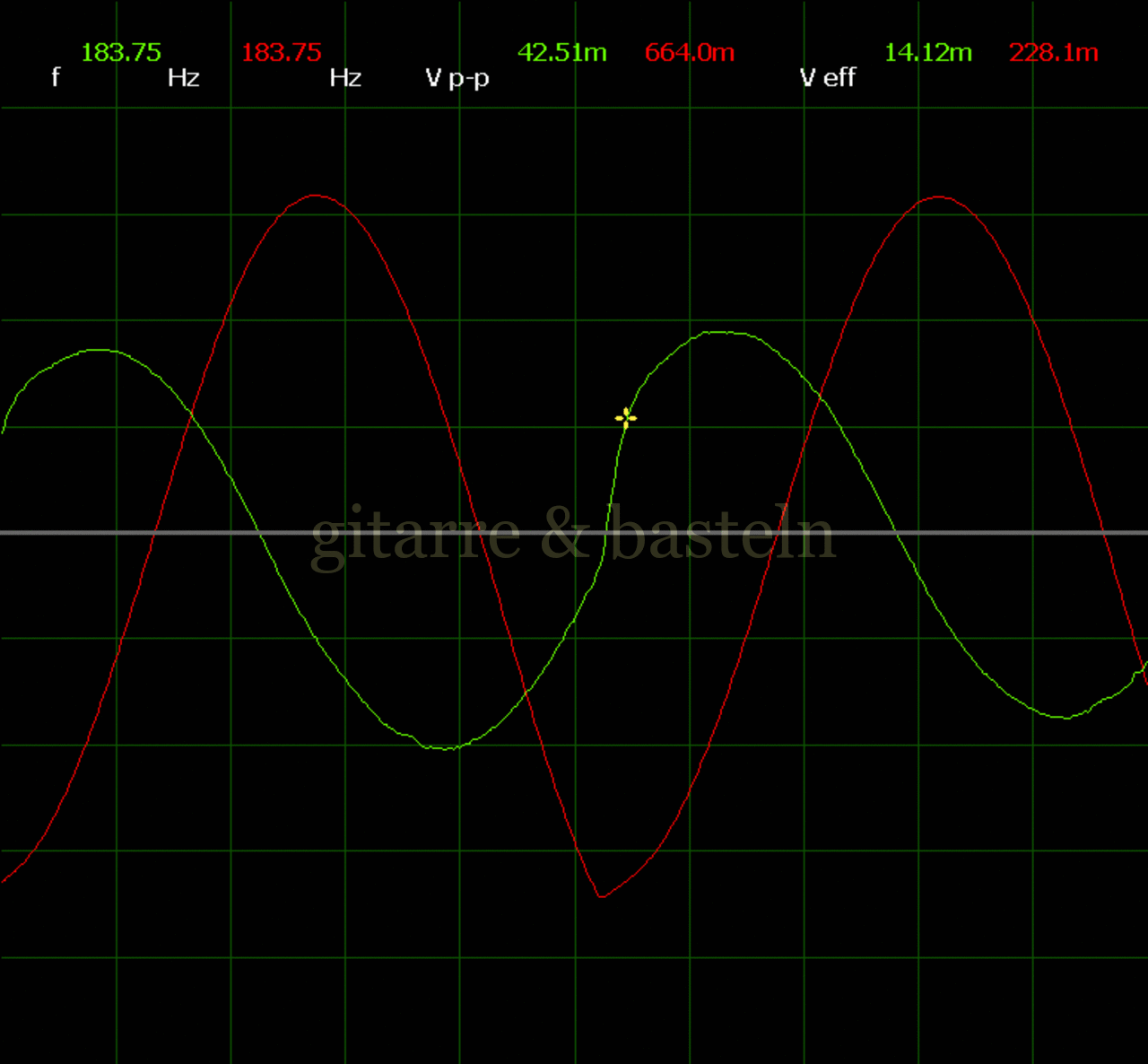
Um einzuschätzen, ob die Anbindung von C19 die „Signalqualität“ des der LFO verbessert, wurde für alle gemessenen Einstellungen auch Oszillogramme erstellt, die in der folgenden Bildertabelle 3.2 zusammengefasst werden:
Bildertabelle 3.2: Oszillogramme, erstellt mit der Testschaltung des LFO entsprechend Schaltplan 3.2.
Die Wirkung von C19 beschränkt sich auf die hohen Schwingfrequenzen, hier wird der Übergang der steil fallenden Flanke in das untere Maximum abgerundet. Es wird also im weiteren sinnvoll sein, die gesamte Steuerschaltung, LFO, Filter und Biastreiber zusammen auf dem Breadboard aufzubauen und zu testen.
Filterschaltung und Treiberstufe nach dem LFO
Kapitelinhalt:[ Überspringen ]- Abschätzen der Kondensatorwerte •
- Filterkondensatoren nach der Treiberstufe •
- Zwischenstand für LFO, Filterschaltung und Treiberstufe •
- Filter mit geringerer Dämpfung
Abschätzen der Kondensatorwerte
Nun wurde also die gesamte Steuerschaltung des Vibrato-Effekts auf dem Breadboard aufgebaut, um – durch Probieren – sinnvolle Werte für die verwendeten Kondensatoren zu finden:
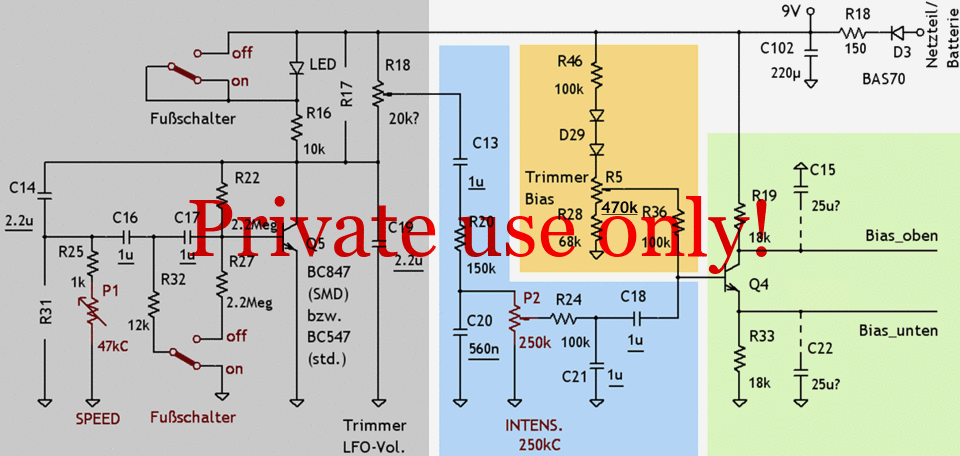

Schaltplan 3.3: Hypothese für LFO (Hintergrund grau), Filter (Hg. blau), Bias-Einstellung (Hg. gelb) und Bias-Treiber (Hg. grün; von links nach rechts) eines Röhren / Halbleiter-Vibrato, orientiert an der Schaltung des Surfy Industries Surfy Vibe. (Unterstrichene Werte hypothetisch.)
Auch in diesem Fall fand für den LFO ein anderer Transistor (BC549C) Verwendung. Die gesamte Schaltung wurde mit einhundertfacher Frequenz (Kondensatoren im LFO einhundert mal so klein) getestet; d. h. auch die anderen Kondensatoren verkleinern sich im Maßstab 1 : 100.
- C19 (Filterkondensator am Ausgang des LFO):
-
Hier wurde schon beim Test der Schaltung des LFO auf 2,2 µF „getippt“.
- C13 (Koppelkondensator hinter dem LFO):
-
In der Originalschaltung waren 1,25 µF gemessen worden; damit ergibt sich ein Hochpass von 0,7 Hz. Auf dem Breadboard wurde ein Wert von 1 µF resp. 10 nF für günstiger gehalten, dann wird der Ausgangspegel des LFO bei den kleinen Frequenzen nicht so ganz so groß.
- C20 (Erster Tiefpass hinter dem LFO):
-
In der Originalschaltung wurde C20 mit 560 nF gemessen. Der Wert wurde im Wesentlichen im Maßstab auf das Breadboard übernommen – zusammengesetzt aus 4,7 nF und 1 nF. Mit der Originalgröße von 560 nF ergibt sich mit den angrenzenden Widerständen R20 (150 kΩ) parallel P2 (250 kΩ) ein Tiefpass von etwa 3 Hz.
- C21 (Tiefpass hinter dem Potentiometer):
-
Der Wert von 1 µF wurde aus den Messungen am Gerät übernommen – auf dem Breadboard entsprechend 10 nF.
- C18 (Zweiter Hochpass hinter dem LFO):
-
C18 dient der Gleichspannungstrennung zum Bias-Trimmer und wurde in der Originalschaltung mit 1,3 nF gemessen. Auch dieser Wert wurde – wie C13 – nicht genau (bzw. im Maßstab) übernommen, eine Korrektur auf 1 µ zur Pegelanpassung der tiefen LFO-Frequenzen schien auch an dieser Stelle sinnvoll.
Filterkondensatoren nach der Treiberstufe
Anschließend ging es um die beiden Kondensatoren hinter der Kathodynschaltung – die Ergebnisse bzw. Schlussfolgerungen sind vergleichbar mit denen bei der Ansteuerungsschaltung des „Harmonic Tremolo“ (siehe hier). Nichtdestotrotz sollen Überlegungen und Messungen für diese Kondensatoren in der Schaltung des Röhren- / Halbleiter-Vibratos kurz dargestellt werden (Bereich ggfs. durch Anklicken auf- oder zuklappen):
Berechnungen und Messungen zu den Filterkondensatoren hinter der Kathodynschaltung. (Zum Öffnen klicken)
Es ist auch in dieser Schaltung nicht klar, wie eine weitere Filterung mit diesen Kondensatoren funktionieren soll: Der Transistor versucht mit dem Emitter dem Signal an der Basis zu folgen. Ein Kondensator parallel zum Sourcewiderstand erhöht dabei mit steigender Frequenz lediglich den Pegel der Signalströme durch den Transistor, während der Kondensator am Drainwiderstand diese Anhebung der höheren Frequenzen im Kollektorstrom wieder entsprechend herausfiltern muss.
Wenn es hier überhaupt eine Tiefpass-Filterwirkung über einen Kondensator geben kann, dann an dem Tiefpass, dass der Kondensator mit dem differentiellen Widerstand zwischen Emitter und Basis bildet (mit dem differentiellen Widerstand, den der Kondensator vom Emitter in Richtung Basis „sieht“). Dieser differentielle Widerstand ist gleich dem Quotienten aus Temperaturspannung (UT = 26 mV) und dem Emitterruhestrom des Transistors.
Bei einem Emitterstrom von etwa 140 µA (gemessene Emitterspannung knapp 2,5 V, Emitterwiderstand 18 kΩ) sähe der Kondensator C22 im Emitter einen differentiellen Widerstand von 26 mV / 0,14 mA ≈ 200 Ω und es entstände ein Tiefpass von etwa 30 Hz.
Auch diese Überlegungen wurden auf dem Breadboard überprüft – nach dem Einfügen von zwei Kondensatoren 220 nF an Emitter und Kollektor von Q4 (entsprechend der Schaltungshypothese in Schaltplan 3.3; Maßstab 1 : 100) wurden bei mittleren Einstellungen des SPEED-Widerstands an Emitter und Kollektor der Kathodynschaltung Asymmetrien des Sinussignals beobachtet. Das heißt, der Transistor übersteuert durch die über den Emitterkondensator angehobenen Emitterströme. Dass es sich um Übersteuerungen handelt, lässt sich daran erkennen, dass die Signale bei sehr kleinem Pegel einigermaßen „manierlich“ aussehen:
Für die beiden Kondensatoren könnte man das diesbezügliche Ergebnis aus dem Artikel zum „Harmonic Tremolo“ übernehmen – beide Kondensatoren sollten (auf der Leiterplatte) schaltbar (gegen Masse) sein, um mögliche Klangveränderungen, die sie in der originalen Röhrenschaltung hervorrufen, nachbilden zu können. Ein Wert von 25 µF ist dabei allerdings unsinnig – hier können die 250 nF aus der Originalschaltung des Magnatone verwendet werden.
Zwischenstand für LFO, Filterschaltung und Treiberstufe
Nach den Überlegungen zu den beiden eigenartigen Kondensatoren hinter der Kathodynschaltung nun eine Zusammenfassung der in der Messschaltung entsprechend Schaltplan 3.3 – gemessenen Werte.
Am Ausgang der Messschaltung wurde ein stark sinus-ähnliches Signal gemessen; allerdings ist eine der beiden Halbwellen (am Kollektor die untere, am Emitter die obere) schmaler und steiler. Ansonsten sind die Signale im Wesentlichen zu ihren Scheitelpunkten symmetrisch.
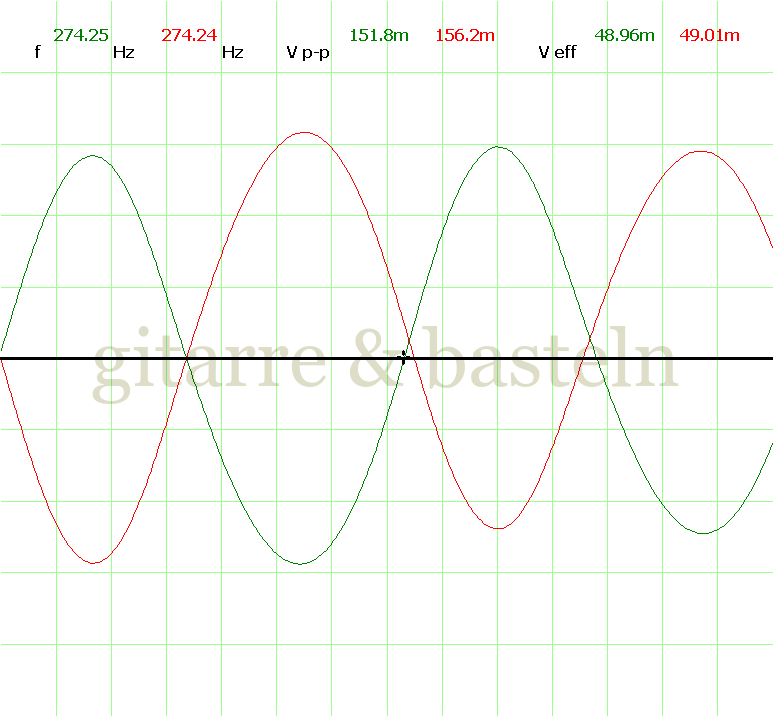
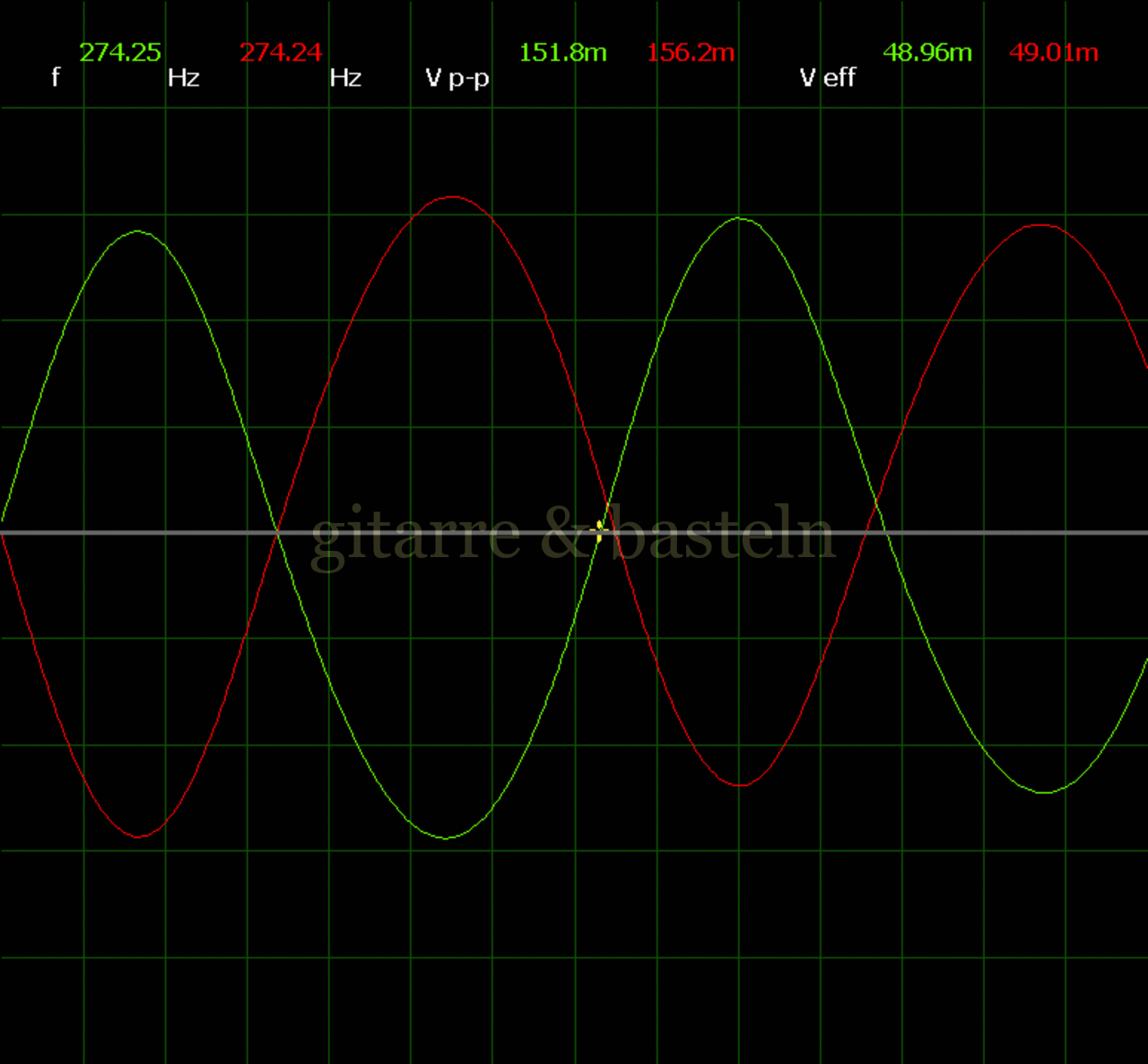
Dazu noch ein paar Oszillogramme für verschiedenen Einstellungen des Speed-Regler-Widerstands:
Bildertabelle 3.4: Oszillogramme am Ausgang der Kathodynschaltung entsprechend Schaltplan 3.3 – ohne Kondensatoren C15 und C22.
Neben den Oszillogrammen wurden auch Messwerte aufgezeichnet (siehe die folgenden Datentabellen). Sie beinhalten – für die sechs verschiedene Einstellungen des Stellwiderstands – die gemessene Frequenz des LFO, gemessene Spannungen (Effektiv- und Spitze-Spitze-Werte) an Emitter und Kollektor von Q4.
Dazu, in der folgenden Tabelle 3.5, die Ergebnisse für die Schaltung ohne Kondensatoren hinter der Kathodynschaltung, entnommen den Oszillogrammen in Bildertabelle 3.4:
| P1 [kΩ] |
fmess [Hz] |
UK [V] |
UE [V] |
||
|---|---|---|---|---|---|
| pp | eff. | pp | eff. | ||
| 1 kΩ | 536 | 0,32 | 0,10 | 0,29 | 0,10 |
| 2,2 kΩ | 438 | 0,53 | 0,17 | 0,51 | 0,17 |
| 4,7 kΩ | 345 | 0,67 | 0,22 | 0,65 | 0,22 |
| 10 kΩ | 274 | 0,79 | 0,27 | 0,76 | 0,26 |
| 22 kΩ | 221 | 0,87 | 0,30 | 0,84 | 0,29 |
| 47 kΩ | 182 | 0,84 | 0,28 | 0,82 | 0,28 |
Filter mit geringerer Dämpfung
Kapitelinhalt:[ Überspringen ]- Pegelverhältnisse in der Filterschaltung •
- Filterschaltung und „gesehene“ Widerstände •
- Filterschaltung mit kleiner Dämpfung •
- Filterschaltung – noch einmal die erste Hypothese •
- Filterschaltung entsprechend dem Magnatone 280B •
- Abschluss und Ausblick
Bei der genaueren Betrachtung der beiden Phasenschieberstufen des Effekts sowie der Frage, wie dort die Varistoren im Magnatone 280B in der JFET-Adaption durch Diodenstrecken ersetzt werden können, fiel der relativ hohe notwendige Biasspannungshub für die Diodenstrecken auf. Für eine Verschiebung der 90°-Frequenz jeder Phasenstufe um zwei Oktaven nach oben und unten (auf ein Viertel bzw. das Vierfache der ursprünglichen Frequenz) ist ein Biasspannungshub von etwa ±1 V erforderlich (siehe Kapitel Berechnungen im Surfy Vibe und dort Diagramm 4.2). Diese Biasspannungshübe werden aber in der Schaltung entstehend der ersten Hypothese (siehe obigen Schaltplan 3.3) nicht erreicht, wie danach in Tabelle 3.5 zu lesen ist.
Dieses Problem scheint es in der Originalschaltung des Magnatone 280B (siehe Schaltplan 3.1) nicht zu geben. Zum einen fällt auf, dass das Ausgangssignal des LFO dort kaum gefiltert wird – dem INTENSITY-Regler folgen zwei Tiefpässe mit einer −3dB-Frequenz zwischen 50 Hz und 100 Hz (erster Tiefpass mit C5, abhängig von der Stellung des INTENSITY-Reglers) und 100 Hz (zweiter Tiefpass mit R9 und C6). Zum anderen war im genannten Kapitel zu den Phasenschieberstufen (siehe Abschnitt Berechnungen im Magnatone) herausgefunden worden, dass für – eine Verschiebung der 90°-Frequenz um jeweils zwei Oktaven nach oben und unten – ein Spannungshub von etwa ±60 V nötig ist. Dieser Hub kann mit einem Röhren-LFO (Ausgangsspannungshub mindestens 150 V Spitze-Spitze) auch erreicht werden, wenn die Filterung nicht allzu stark sein muss.
Dabei kann es natürlich sein, dass das Ausgangssignal eines Röhren-LFO schon deutlicher sinusähnlich ist und gar nicht so stark gefiltert werden muss.
Insgesamt muss also in Erwägung gezogen werden, dass die Kondensatorwerte in Schaltplan 3.1 zu groß geschätzt wurden und das entstehende gefilterte Modulationssignal zu schwach ist.
Pegelverhältnisse in der Filterschaltung
Insofern ist es sinnvoll, diese Schaltung im Hinblick der Pegelverhältnisse wie auch im Hinblick auf die Widerstände, die die Kondensatoren „sehen“, noch einmal genauer zu betrachten (siehe folgenden Schaltplan 3.4):


Schaltplan 3.4: Ersatzschaltbild von Widerständen und Pegelverhältnissen in der Filtersektion der hypothetischen Schaltung nach Schaltplan 3.3
Von hinten, d. h. vom Anschluss uA in die Filterschaltung hineingesehen, „sieht“ uA zum einen R36 und den Ausgangswiderstand des Biasspannungsteilers um R5 – dieser Gesamtwiderstand soll R36+ heißen:
\( \begin{eqnarray} R_{\textrm{36}+} & = & R_{\textrm{36}} + \left( r_{\textrm{d,29}} + R_{\textrm{36}} + R_{\textrm{5,links}} \right) {\Big|} {\Big|} \left( R_{\textrm{5,rechts}} + R_{\textrm{28}} \right) \\~\\ & = & 100\,\textrm{kΩ} + 410\,\textrm{kΩ} \,{\Big|} {\Big|} \,238 \,\textrm{kΩ} \\~\\ & \approx{} & 150 \,\textrm{kΩ} \tag{3.1}\end{eqnarray} \)
Für einen maximalen Pegel von uA, d. h. für die minimale Dämpfung ohne Kondensatoren (wenn C13 und C18 kurzgeschlossen sowie C20 und C21 nicht vorhanden wären) und mit maximalem INTENSITY-Regler P2 ergäbe sich so ein Spannungsverhältnis zwischen Filterausgangsspannung uA und der Ausgangsspannung uC,5 des LFO:
\( \begin{eqnarray} \!\!\frac{u_{\textrm{A}}}{u_{\textrm{C,5}}}\! & = & \frac{P_2\,{|}{|} \left( R_{24} + R_{36+} \right) } {R_{20} + P_2\,{|}{|} \left( R_{24} + R_{36+} \right) } \cdot{} \frac{R_{36+}} {R_{24} + R_{36+} } \\~\\ & & \textrm{(alle Widerstände in kΩ):} \\~\\ & \approx & \frac{ 250\,{|}{|} \left( 100 + 150 \right) } {150 + 250\,{|}{|} \left( 100 + 150 \right) } \cdot{} \frac{150} {100 + 150 } \\~\\ & \approx & \frac{125} {275} \cdot{} \frac{150} {250} \\~\\ & \approx & 0{,}27 \tag{3.2}\end{eqnarray} \)
Bei einem Ausgangsspannungshub des LFO von etwa 7 V (siehe Tabelle 3.1) betrüge der maximale Biasspannungshub uA,pp,max ohne Filterung etwa 1,9 V Spitze-Spitze. Für eine Mindestbiasspannungshub von 1 V Spitze-Spitze muss die maximale Filterdämpfung kleiner als 6 dB sein. Das könnte dadurch erreicht werden, dass die −3dB-Frequenzen der beiden Hoch- und Tiefpässe (Hochpässe an C13 und C18, Tiefpässe an C20 und C21) nur jeweils an den Frequenzbereich des LFO heranreichen.
Filterschaltung und „gesehene“ Widerstände
Die Kondensatoren C13, C18, C20 und C21 sollte also so groß sein, dass sie mit den umgebenden Widerständen (die Widerstände bzw. Impedanzen, die die Kondensatoren „sehen“), zwei Hochpässe mit einer −3dB-Frequenz von etwa 2 Hz und zwei Tiefpässe mit einer −3dB-Frequenz von etwa 8 Hz bilden. Da die Schaltung insgesamt ein wenig unübersichtlich ist, wurde einmal aufgelistet, welche „Umgebungswiderstände“ die einzelnen Filterkondensatoren in ihrer Umgebung sehen (und zwar abhängig von der Stellung des INTENSITY-Reglers R5) – die folgende Tabelle 3.6 trägt diese Informationen zusammen:
| R5 | C13 „sieht“ [kΩ] |
C20 „sieht“ [kΩ] |
C18, C21 „sehen“ [kΩ] |
|||
|---|---|---|---|---|---|---|
| ← | → | ← | → | ← | → | |
| links | ≈ 10 | ≈ 300 | ≈ 160 | ≈ 150 | ≈ 200 | ≈ 250 |
| Mitte | ≈ 10 | ≈ 370 | ≈ 160 | ≈ 220 | ≈ 190 | ≈ 250 |
| rechts | ≈ 10 | ≈ 400 | ≈ 160 | ≈ 250 | ≈ 100 | ≈ 250 |
| Gesamt | 310 – 410 kΩ | 310 – 410 kΩ |
C18: 350 kΩ – 450 kΩ
C21: 70 kΩ – 110 kΩ |
|||
Zu den beiden letzten Spalten (betreffend C18 und C21) wäre natürlich anzumerken, dass der Hochpasskondensator C18 mit den anschließenden Widerständen in Serie geschaltet wird, während C21, der Tiefpasskondensator gegen Masse, die anschließenden Impedanzen parallelgeschaltet sieht.
Filterschaltung mit kleiner Dämpfung
Zunächst wurde versucht, eine Filterschaltung zu finden, die eine möglichst geringe Dämpfung hat. Dazu wurden die −3dB-Frequenzen der Hochpasskondensatoren auf die tiefste und die der Tiefpasskondensatoren auf die höchste LFO-Frequenz gelegt. Dazu wurde der Frequenzgang dieser Schaltung ermittelt – der folgende Schaltplan 3.5 zeigt die Simulationsschaltung und Diagramm 3.2 das Ergebnis.
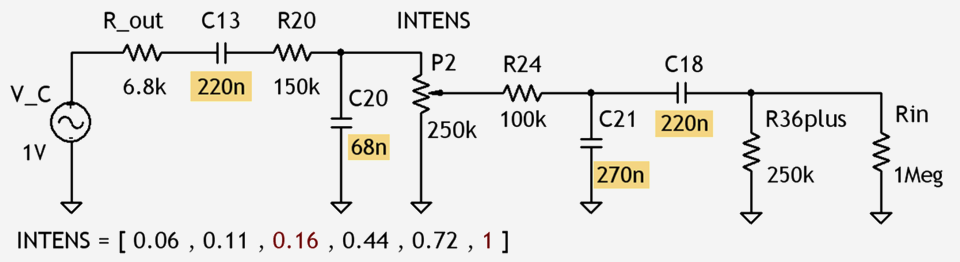

Schaltplan 3.5: Testschaltung für ein Filter geringer Signaldämpfung.
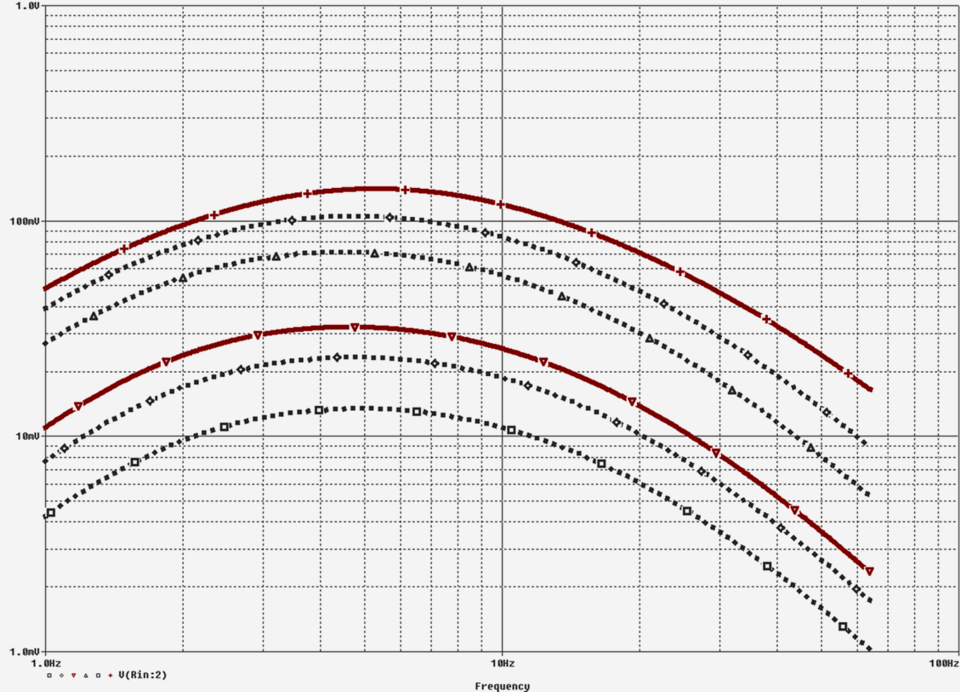

Diagr. 3.2: Ergebnis der Simulation der Schaltung nach Schaltplan 3.5 – Frequenzgang der Spannungen am Ausgang des Filters, abhängig von der Einstellung des INTENSITY-Reglers.
Zwischen zwei und sechs Hertz ist der Graph des Frequenzgangs relativ eben und die Dämpfung der Filterschaltung liegt bei etwa 1:10 (Signalgenerator VC mit einem Pegel von 1 V; im Diagramm Ausgangspegel des Filters zwischen etwa 120 mV und 150 mV).
Blieb die Überprüfung der gesamte Schaltung am Breadboard (wieder im Frequenzmaßstab 1:100) – Schaltplan 3.6 zeigt den Aufbau auf dem Breadboard und die darauffolgende Bildertabelle 3.7 die Oszillogramme für sechs verschiedene Einstellungen des SPEED-Reglers:
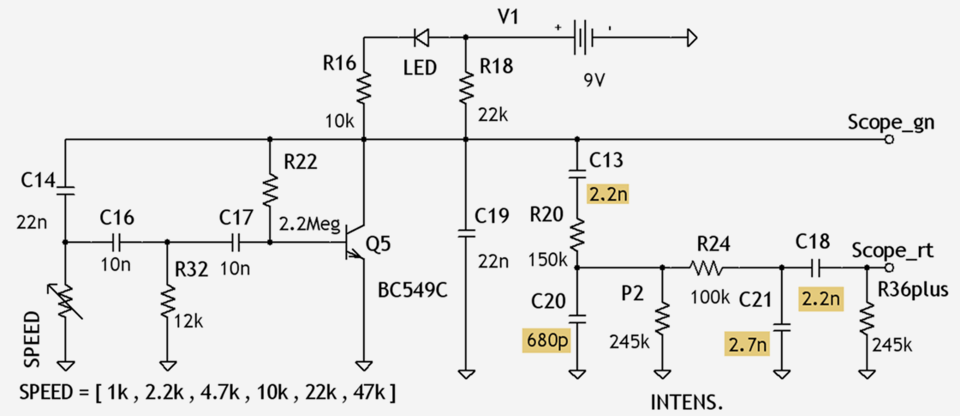

Schaltplan 3.6: Testschaltung von LFO und Filter entsprechend Schaltplan 3.5 – aufgebaut auf dem Breadboard und im Frequenzmaßstab 1 : 100.
Bildertabelle 3.7: Oszillogramme am Ausgang der Filterschaltung entsprechend Schaltplan 3.6. (Zum Schließen klicken)
Das ist nun ein eher weniger gutes Ergebnis – für die mittleren Frequenzen / Einstellungen des SPEED-Reglers entsteht am Ausgang des Filters eine Art asymmetrisches Dreiecks (bzw. in der Tendenz ein Sägezahnsignal).
Die Ausgangsspannungshübe des gefilterten LFO-Signals entsprechen allerdings durchaus den oben genannten Erwartungen (ein Ausgangsspannungshub von etwa einem Volt).
| R31+P1 [kΩ] |
f [Hz] |
uC [V] |
ufilt. [V] |
||
|---|---|---|---|---|---|
| pp | eff. | pp | eff. | ||
| 1 kΩ | 534 | 5,92 | 2,1 | 0,89 | 0,30 |
| 2,2 kΩ | 434 | 6,82 | 2,4 | 1,02 | 0,33 |
| 4,7 kΩ | 342 | 7,12 | 2,5 | 1,06 | 0,34 |
| 10 kΩ | 273 | 7,06 | 2,6 | 1,02 | 0,32 |
| 22 kΩ | 223 | 7,34 | 2,6 | 0,88 | 0,28 |
| 47 kΩ | 184 | 6,65 | 2,3 | 0,65 | 0,22 |
Filterschaltung – noch einmal die erste Hypothese
Zwischenzeitlich wurden auch noch einmal die zuerst gefundenen Werte für die Filterkondensatoren ( siehe obige Schaltplan 3.3) in die Filterschaltung eingesetzt – zunächst in der Simulation (siehe die Simulationsschaltung in Schaltplan 3.7 und den ermittelten Frequenzgang in Diagramm 3.3)
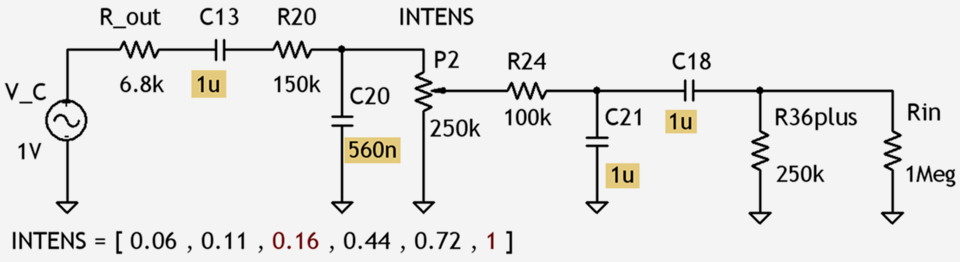

Schaltplan 3.7: Testschaltung für ein Filterdesign entsprechend der ersten gefundenen Schaltungshypothese (siehe Schaltplan 3.3).
Im Ergebnis der Amplitudengang des Filters:
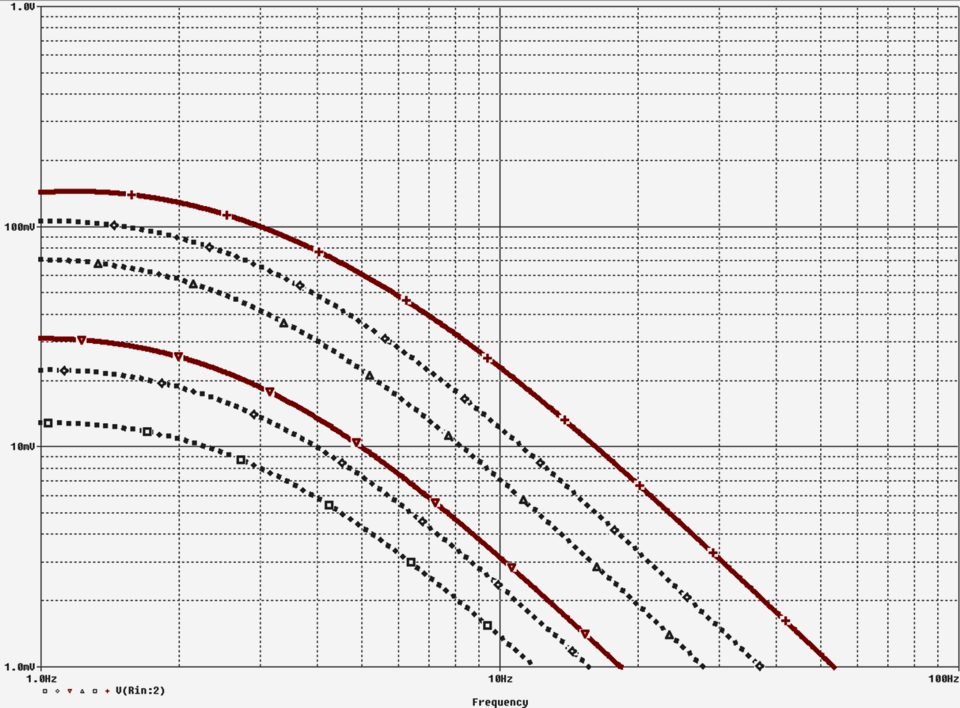

Diagr. 3.3: Ergebnis der Simulation der Schaltung nach Schaltplan 3.7 – Frequenzgang der Spannungen am Ausgang des Filters, abhängig von der Einstellung des INTENSITY-Reglers.
Im Frequenzbereich des LFO (etwa 2 Hz bis 8 Hz) fällt die Amplitude hinter dem Filter etwa reziprok zur Frequenz – der Ausgangspegel des Filters liegt aber, bei einem Ausgangspegel uC des Signalgenerators von 1 V, im relevanten Frequenzbereich von 2 Hz bis 8 Hz, unter 100 mV.
Nichtdestotrotz wurden auch hiermit einem Breadboard-Aufbau entsprechend des folgenden Schaltplan 3.8 Oszillogramme erstellt und die gemessenen Werte in der nachfolgenden Bildertabelle 3.9 zusammengefasst.
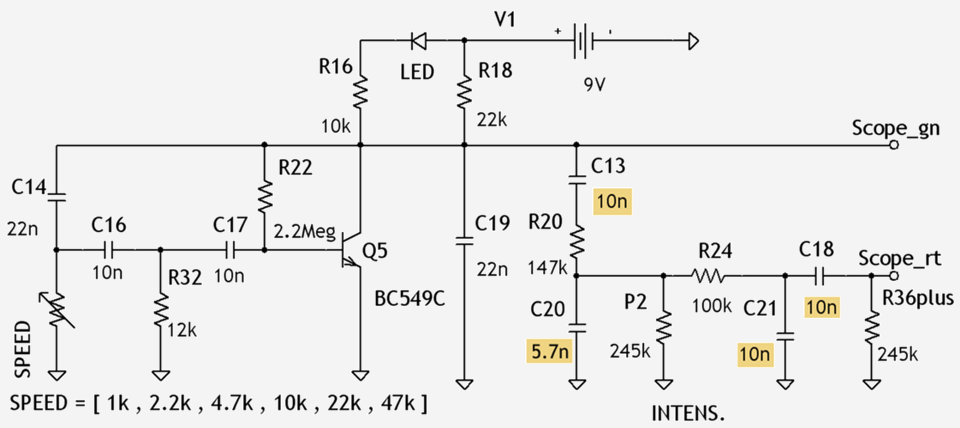

Schaltplan 3.8: Testschaltung von LFO und Filter entsprechend Schaltplan 3.7 – aufgebaut auf dem Breadboard und im Frequenzmaßstab 1 : 100.
Bildertabelle 3.9: Oszillogramme am Ausgang der Filterschaltung entsprechend Schaltplan 3.8. (Zum Schließen klicken)
Im Ergebnis ist alles wie gehabt, das Steuersignal hinter dem Filter ist „schön“ genug, aber der Pegel ist möglicherweise zu klein.
| R31+P1 [kΩ] |
f [Hz] |
uC [V] |
ufilt. [V] |
||
|---|---|---|---|---|---|
| pp | eff | pp | eff | ||
| 1 kΩ | 528 | 5,6 | 1,0 | 0,35 | 0,11 |
| 2,2 kΩ | 436 | 6,6 | 2,3 | 0,49 | 0,16 |
| 4,7 kΩ | 344 | 6,8 | 2,4 | 0,65 | 0,21 |
| 10 kΩ | 274 | 7,0 | 2,5 | 0,79 | 0,26 |
| 22 kΩ | 224 | 7,1 | 2,5 | 0,89 | 0,30 |
| 47 kΩ | 184 | 6,4 | 2,2 | 0,88 | 0,30 |
Somit bleibt noch die Möglichkeit, mit den Werten für die Kondensatoren C13, C18, C20 und C21 das Filterdesign der Originalschaltung nachzubilden.
Filterschaltung entsprechend dem Magnatone 280B
An dieser Stelle ist dann ein Blick auf die Originalschaltung (siehe Schaltplan 3.1 bzw. auf den folgenden Schaltplan 3.9, der die Filterschaltung hinter dem LFO in einer Simulationsschaltung zusammenfasst), sinnvoll.
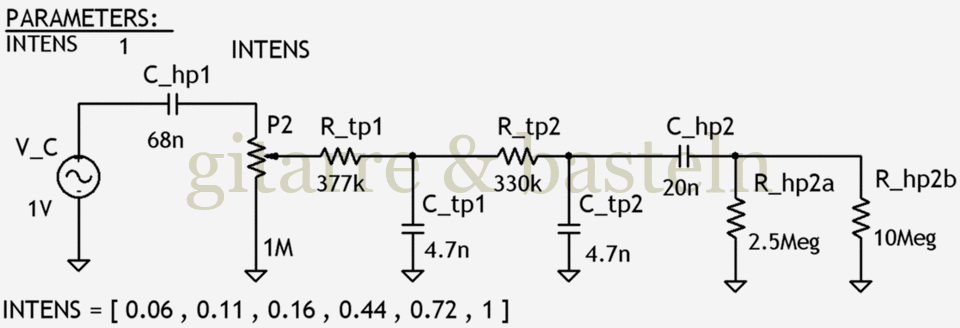

Schaltplan 3.9: Filterschaltung des LFO-Signals im Magnatone 280B.
Letztgenannte Schaltung wurde simuliert – das folgende Diagramm 3.4 zeigt das Ergebnis der Simulation:
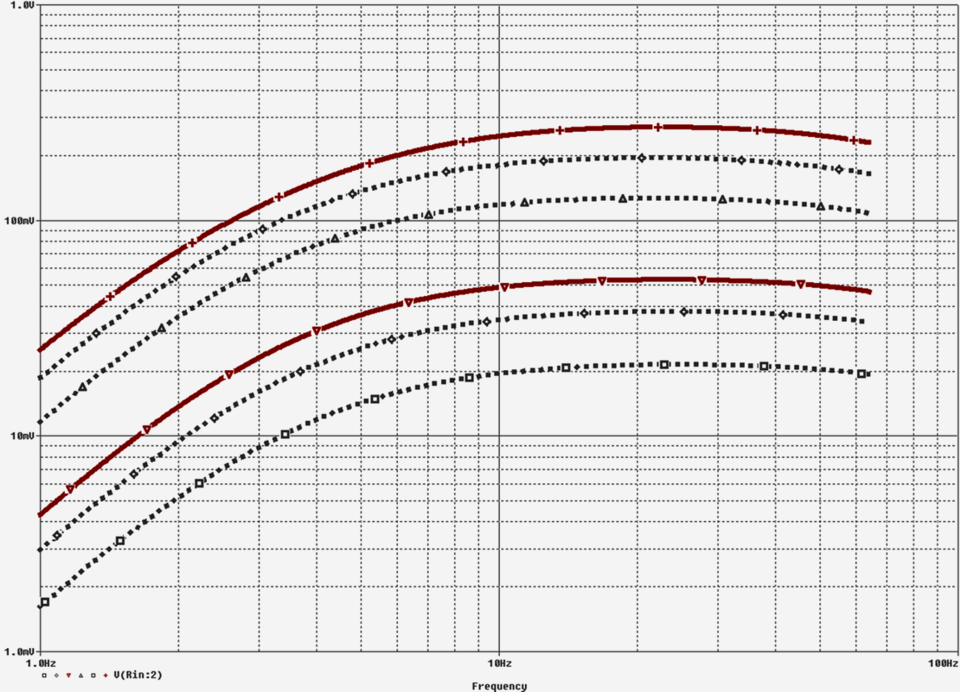

Diagr. 3.4: Ergebnis der Simulation der Schaltung nach Schaltplan 3.9 – Frequenzgang der Spannungen am Ausgang des Filters, abhängig von der Einstellung des INTENSITY-Reglers.
Das Ergebnis zeigt die Wirkung von Hochpässen mit −3dB-Frequenzen bei etwa 5 Hz, und die von Tiefpässen mit −3dB-Frequenzen weit über 100 Hz.
Will man für dieses Filterverhalten Werte für die Kondensatoren C13, C18, C20 und C21 ermitteln, d. h. soll diese Schaltung in die im Surfy Vibe gefundene Struktur (entsprechend Schaltplan 3.4) umgeformt werden, muss man im Frequenzgang nach Ähnlichkeiten suchen. Im Surfy Vibe wie in der Filterschaltung im Magnatone 280B sind zwei Hochpässe (mit C4 = 68 nF und C7 = 20 nF) und zwei Tiefpässe (mit C5 = C6 = 4,7 nF) zu finden:
- Hochpass mit C4:
-
C4 = 68 nF sieht mindestens 750 kΩ ( P2 || [ R7 + R8 + R9 + ( R10 || R11)]) – das läuft auf einen Hochpass von etwa 3 Hz hinaus.
- Hochpass mit C7:
-
C7 = 20 nF sieht hier den Eingangswiderstand der nachfolgenden Stufe – hier bestimmt der Spannungsteiler zwischen Kondensator und Röhre den Eingangswiderstand (R10 || R11 = 3,3 MΩ || 10 MΩ ≈ 2,5 MΩ); es entsteht ebenfalls ein Hochpass von 3 Hz.
- Tiefpässe mit C5 und C6:
-
Beide Kondensatoren sehen Widerstände 330 kΩ – bei 4,7 nF ergibt sich ein Tiefpass von 100 Hz, der für den geplanten Frequenzbereich irrelevant ist.
Nichtdestotrotz lassen sich mit diesen Angaben sinnvolle Kondensatorwerte für C13, C18, C20 und C21 finden. Die folgende Schaltplan 3.10 zeigt das Ergebnis der Überlegungen.


Schaltplan 3.10: Testschaltung für ein Filterdesign, das den Vorgaben aus der Originalschaltung des Magnatone 280B entspricht.
Das Ergebnis dieser Simulation hingegen stellt das folgende Diagramm 3.5 dar:


Diagr. 3.5: Ergebnis der Simulation der Schaltung nach Schaltplan 3.10 – Frequenzgang der Spannungen am Ausgang des Filters, abhängig von der Einstellung des INTENSITY-Reglers.
Wie zu erwarten, arbeitet das Filter im Wesentlichen als Hochpass – die Frequenzabsenkung ab 100 Hz fällt für die Ausgangsfrequenzen des LFO nicht ins Gewicht.
Dazu dann der Schaltplan für die Messungen auf dem Breadboard


Schaltplan 3.11: Testschaltung von LFO und Filter entsprechend Schaltplan 3.10 – aufgebaut auf dem Breadboard und im Frequenzmaßstab 1 : 100.
und die Bildertabelle mit den mit obiger Schaltung erstellten Oszillogrammen:
Bildertabelle 3.11: Oszillogramme am Ausgang der Filterschaltung entsprechend Schaltplan 3.11. (Zum Schließen klicken)
Das kann wohl nur als verheerend bezeichnet werden – die „Macken“, die im Ausgangssignal des LFO aufgefallen waren, wurden in diesem Filter nicht ausgebügelt, sondern noch verschlimmert.
Abschluss und Ausblick
Somit ist es eher unwahrscheinlich, dass Surfy Industries das Design des Filters hinter dem LFO so übernommen hat.
Es kann allerdings sein, dass das auch gar nicht sinnvoll ist – wenn nämlich das Ausgangssignal des Röhren-LFO schon von sich aus wesentlich „schöner“ und sinus-ähnlicher ist als das eines Transistor-LFO, dann wäre z. B. im Magnatone 280B auch kein so stark den Pegel dämpfendes Filter nötig oder zumindest keine sinnvolle Referenz für ein Filter hinter einem Transistor-LFO.
Um jetzt der schaltungstechnischen „Wahrheit“ – zumindest der im Magnatone 280B näher zu kommen, müsste man einen realen Röhren-LFO und die bekannte Filterschaltung ausmessen oder ihn zumindest simulieren und die Oszillogramme der gefilterten Signale anschauen und messen, um überhaupt zu wissen, welche Signale und Signaleigenschaften von Röhren-LFO und Filter nachgebildet werden müssen und welche Amplituden für einen sinnvollen Effektnachbau notwendig sind.
Bis dahin bleibt wohl nur, die erste gefundene hypothetische Schaltung entsprechend Schaltplan 3.3 auszuprobieren …
Der Bias für das Stellglied
Kapitelinhalt:[ Überspringen ]- Wer misst misst Mist? – plausible Widerstandswerte •
- Versuch einer Temperaturkompensationsschaltung
Last but not least zum „gelben Teil“ von Schaltplan 3.3 – der Bias-Schaltung für die Vorspannung der Diodenstrecken.
Prinzipiell keine ungewöhnliche Schaltung. Aus der um die Flussspannung zweier Schaltdioden verminderten Betriebsspannung (R46 und die doppelte Schaltdiode D29 könnten auch in umgekehrter Reihenfolge angeordnet werden) wird durch einen einfachen Spannungsteiler die Basisvorspannung der Treiberstufe um Q4 abgeleitet. Aus dieser Basisvorspannung leitet sich die Ruhespannung zwischen Emitter und Kollektor von Q4 ab – zwischen Emitter und Kollektor von Q4 liegen dann die Diodenstrecken in Serie mit ihren Vorwiderständen.
Wer misst misst Mist? – plausible Widerstandswerte
Bei der Erforschung der JFET-Adaption des Magnatone mussten erst einmal plausible Werte für die Widerstände herausgefunden werden. Das war im Falle des Trimmers R5 nicht so einfach. An einem Testpunkt 4 (oberes Ende von R5) war eine Spannung von 6,4 V sowie eine Betriebsspannung von 9,2 V gemessen worden. Das lässt (für beide Dioden von D29 eine Flussspannung von 0,5 V angenommen) auf einen Strom durch R46 und den gesamten Biasspannungsteiler von etwa 18 µA schließen (9,2 V − 6,4 V − 2 ⋅ 0,5 V; geteilt durch 100 kΩ). Der Trimmer R5 müsste dann einen Widerstand von etwa 290 kΩ haben ( 6,4 V dividiert durch 18 µA; abzüglich R28 = 68 kΩ), was wenig sinnvoll erscheint.
Sinnvoller scheint es aber, dass das Messergebnis an Testpunkt 4 durch das Messinstrument verfälscht wurde – ein einfaches Voltmeter mit einem Eingangswiderstand von 1 MΩ zieht bei einer gemessenen Spannung von 6,4 V auch 6,4 µA aus dem Testpunkt. Demzufolge wäre die Spannung an Testpunkt 4 etwa 600 mV größer.
Eine plausible Schätzung ist in Schaltplan 3.3 bereits eingetragen – bei einem Wert für R5 von 470 kΩ würde sich die um die Flussspannung von D29 verringerte Betriebsspannung (9,2 V abzüglich 2 ⋅ 0,5 V) auf R46 = 100 kΩ, R5 = 470 kΩ und R28 = 68 kΩ aufteilen. Auch auf diesem Weg ergäbe sich so an dem (durch Messungen unbelasteten) Testpunkt 4 eine Ruhespannung von etwa 7 V, was obige Schätzung für R5 = 470 kΩ plausibel macht. Für den Strom durch den Biasspannungsteiler ergäben sich etwa 11 µA.
Versuch einer Temperaturkompensationsschaltung
Welche Funktion aber hat diese Doppeldiode BAW99? Es wird vermutet, dass es sich hier um eine Temperaturkompensation handelt. Um das zu überprüfen, ist zunächst ein Blick auf die Kennlinie sinnvoll – siehe dazu folgendes Diagramm 3.6:
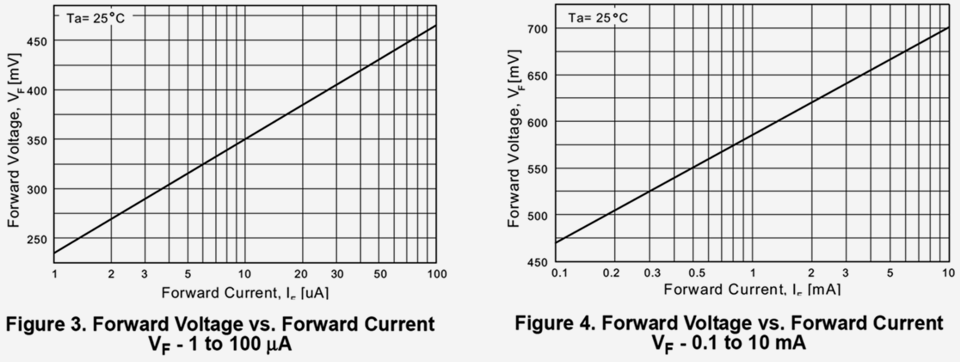

Diagr. 3.6: Statische Kennlinie einer Diode der Doppeldiode BAW99 – Faksimile aus dem Datenblatt des Herstellers ON Semiconductors [ baw ].
Diese (mit Sicherheit stark idealisierte) Kennlinie zeigt, dass die Spannung über jeder der beide Dioden der Doppeldiode bei einem Diodenstrom von 11 µA, etwa 360 mV groß ist; auf der Doppeldiode fallen also etwa 720 mV ab. Das ist zwar etwas weniger, als in den obigen Abschätzungen zum Wert von R5 angenommen, stellt aber die dort angestellten Überlegungen nicht in Frage.
Weiterhin steigt die Spannung über der Doppeldiode bei einer Erhöhung der absoluten Temperatur um 10% (z. B. von 295 K bzw. 25 °C auf von 320,5 K bzw. 54,5 °C; das könnte in einem dunklen Effektgerät, das in der Sonne liegt, durchaus passieren) ebenfalls um 10%.
Zusammenhang zwischen absoluter Temperatur und Spannung über D29: (Zum Öffnen klicken)
Der in obigen Diagrammen idealisiert dargestellte Zusammenhang zwischen Diodenstrom und Diodenspannung lässt sich durch die Shockley-Gleichung darstellen:
\( \begin{eqnarray} I_{\textrm{D}} & = & I_{\textrm{S}} \cdot{}\! \left[ \exp{ \left( \frac{U_{\textrm{D}}} {U_{\textrm{T}}\cdot{}η} \right) - 1 } \right] \\~\\ I_{\textrm{D}} & = & I_{\textrm{S}} \cdot{} \exp{ \left( \frac{U_{\textrm{D}}} {U_{\textrm{T}}\cdot{}η} \right) } - I_{\textrm{S}} \tag{3.3}\end{eqnarray} \)
(Dabei ist IS der sogenannte Sperrstrom der Diode , UT die sogenannte Raumspannung (bei Zimmertemperatur etwa gleich 26 mV) und η eine materialabhängige Konstante (bei Silizium etwas unter zwei).)
Die Raumspannung UT wiederum ändert sich proportional mit der (absoluten) Temperatur.
Da sich, im gegebenen Fall, der Strom durch die Diode kaum ändert (es sei denn, die Betriebsspannung ändert sich drastisch), dürfte eine Änderungen der Temperatur über eine Änderung der Temperaturspannung zu einer Änderung der Diodenspannung führen. Insofern ist es sinnvoll, die Shockley-Gleichung entsprechend umzustellen:
\( \begin{eqnarray} \frac{U_{\textrm{D}}} {U_{\textrm{T}}\cdot{}η} & = & \ln{ \left( \frac{I_{\textrm{D}} + I_{\textrm{S}}} {I_{\textrm{D}}} \right) } \\~\\ U_{\textrm{D}} & = & U_{\textrm{T}} \cdot{} η \cdot{} \ln{ \left( \frac{I_{\textrm{D}} + I_{\textrm{S}}} {I_{\textrm{D}}} \right) } \tag{3.4}\end{eqnarray} \)
Für die Raumspannung UT wiederum ist bekannt:
\( \begin{eqnarray} U_{\textrm{T}} & = & \frac{k\cdot{}T} {q} \tag{3.5}\end{eqnarray} \)
(Hier ist k die sogenannte Boltzmannkonstante, T die Raumtemperatur bzw. die Temperatur der Diode als absolute Temperatur, d. h. bezogen auf den absoluten Nullpunkt, und q die sogenannte Elementarladung.)
Wichtig ist hier lediglich, dass UT proportional zur absoluten Temperatur ist. Daraus lässt sich ableiten:
\( \begin{eqnarray} U_{\textrm{T}} & = & \frac{k\cdot{}T} {q} \\~\\ U_{\textrm{T,1}} & = & \frac{k\cdot{}T_1} {q} \\~\\ U_{\textrm{T,2}} & = & U_{\textrm{T,1}}\cdot{} \frac{T_2} {T_1} \\~\\ U_{\textrm{D2}} & = & U_{\textrm{T,2}}\cdot{} η\cdot{} \ln{ \left( \frac{I_{\textrm{D}} + I_{\textrm{S}}} {I_{\textrm{S}}} \right) } \\~\\ & = & U_{\textrm{D1}}\cdot{} \frac{T_2} {T_1} \tag{3.6}\end{eqnarray} \)
Im konkreten Fall würde also die Spannung am Testpunkt 4 um 10% von 720 mV, d. h. um 72 mV fallen. Diese Spannungsänderung wird nun noch durch die Spannungsteiler um den Trimmer R5 geteilt – genauso, wie von der Ruhespannung von etwa 7 V an Testpunkt 4 noch etwa 3 V an der Basis von Q4 „übrigbleiben“, steigt auch die Basisruhespannung von Q4 durch die Temperaturerhöhung voraussichtlich um etwa 30 mV. Die Spannung zwischen Emitter und Kollektor von Q4 stiege dann um 60 mV, so dass die Spannung über jeder Reihenschaltung von Diodenstrecke und Vorwiderstand um 30 mV erhöht.
Um die Betrachtungen nicht allzu kompliziert zu machen, wurden in EXCEL mit den bekannten Daten der in den Diodenstrecken verwendeten Schottkydiode BAS70-04 für die gesamten Diodenstrecken berechnet; und zwar jeweils für Raumtemperatur (25 °C; UT = 26 mV) und für eine Temperatur von 55 °C (UT = 28,6 mV). Die Daten der BAS70-04 (IS = 0,18µA, η = 1,02) waren vom Autor gemessen worden – siehe dazu auch das Kapitel Diodenauswahl im Surfy Vibe.
Dabei zeigen die Kennlinien den Zusammenhang zwischen der Biasspannung und dem Diodenstrom sowie den zwischen Biasspannung und dem signalbezogenen differentiellen Widerstand der Diodenstrecke (siehe das folgende Diagramm 3.7):
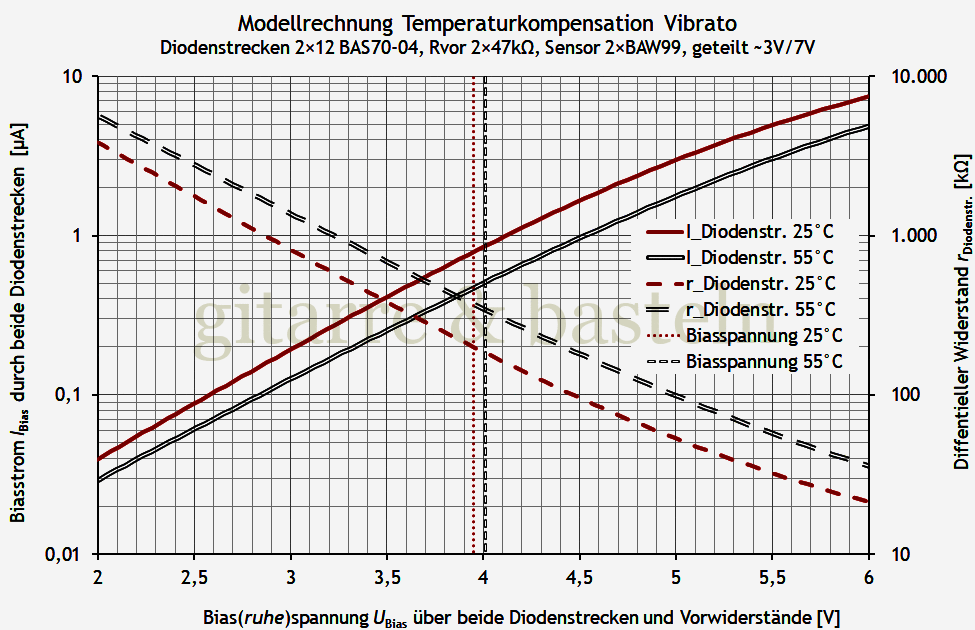

Diagr. 3.7: Ergebnis einer Modellrechnung zur Temperaturkompensation in Schaltung entsprechend Schaltplan 3.3. Angenommene Biasspannungen (Emitter zu Kollektor Q4): 3,95 V für 25°C und 4,01 V für 55°C.
Die senkrechten Linien in obigem Diagramm wiederum markieren eine angenommene Bias(ruhe)spannung für 25 °C (3,95 V) und die um 60 mV höhere Bias(ruhe)spannung für 55 °C.
Es scheint so, dass die Kennlinienverschiebung (im Diagramm: von rot auf doppelt schwarz) durch eine Temperaturerhöhung um bspw. 30° K eine Erhöhung der Biasspannung um mehrere hundert Millivolt erfordern würde, und eine Biasspannungserhöhung von lediglich 60 mV durch zwei Dioden vor dem Biasspannungsteiler dazu nicht ausreicht.
Literatur
- [ magnatone ]
-
Schaltplan des Magnatone 280B. Gefunden auf der Magnatone-Seite http://www.magnatoneamps.com; Downloadlink: http://www.magnatoneamps.com/schematics/magnatone_280B.png.
- [ baw ]
-
Datenblatt der Doppeldiode BAW99 des Herstellers ON Semiconductors