Kolophon
Kolophon – (Technische) Bildbearbeitung
Kapitelinhalt:[ Überspringen ]Nach der eher anschaulichen Darstellung, wie einige der Artikelvignetten entstanden sind, wird es jetzt deutlich trockener und abstrakter – es geht um die Aufbereitung von Oszillogrammen (Screenshots, Ausschneiden, Umfärben, Kleinrechnen und Wasserzeichen) sowie von Artikelbildern und Illustrationen (Zeichnungen vs. Screenshots, Gut- und Schönrastern, Kleinrechnen und Wasserzeichen):
Erstellen der Oszillogramme
Kapitelinhalt:[ Überspringen ]- Anforderungen •
- Programme und Abläufe •
- Screenshots erstellen und Beschneiden •
- Invertieren und nicht Farbinvertieren •
- Skalieren und „Fettrechnen“ •
- „Sourcesets“ und Bildertabellen
Anforderungen
Es bestand der Wunsch, Reihen von Oszillogrammen (Zeitfunktionen, Lissajous-Figuren, Spektren) tabellarisch dargestellt in die Seite einzubinden. Das verwendete Oszilloskop-Programm, Christian Zeilitz' „Soundcard Oscilloscope“, ließ (zumindest in der Testversion) keinen Datenexport von Messwerten zu, so dass mit Screenshots gearbeitet werden muss. Für diese Screenshots sind folgende Bearbeitungsschritte nötig:
- Sammeln und mit Namen versehen:
-
Die Screenshots werden mit dem Windows-Programm
Irfanviewgesammelt; dabei werden systematisch sinnvolle Dateinamen vergeben (die bspw. unterschiedliche Stellgrößen und / oder Schaltungseinstellungen beinhalten und auf den Bildtyp – bspw. auf „_osc“ oder „_osc“ – enden). Dieser Vorgang erfordert Fleiß und ist bis jetzt nicht sinnvoll automatisierbar. - Ausschneiden:
-
Das Oszillogramm ist nur ein Teil des Screenshots und muss ausgeschnitten werden. Das händische Ausschneiden ist eine ziemliche Fummelei, deswegen sollte automatisiert ausgeschnitten werden. Dazu sollten für jeden Monitor und jeden Typ des Programmfensters (Oszillogramm, Lissajous-Figur, Spektrum) die Koordinaten notiert und mit in eine entsprechende Konfigurationsdatei eingetragen werden.
- Invertieren, aber nicht Farbinvertieren:
-
Die Oszillogramme haben einen schwarzen Hintergrund, was für eine Internetseite, insbesondere dann, wenn sie vielleicht ausgedruckt werden soll, ungünstig ist – die Bilder sollten invetiert werden. Gleichzeitig sollen die Farben der Graphen (rot und grün) nicht zu den Komplementärfarben Cyan und Magenta farbinvertiert werden.
- Verkleinern und „fettrechnen“:
-
Die Screenshots müssen deutlich verkleinert werden, ohne dass die relativ feinen Graphen zu dünn werden, soll heißen, die Graphen müssen irgendwie „fettgerechnet“ werden. Das heißt, die Oszillogramme sollen im Browser (zum Beispiel in einem sogenannten Sourceset) in mehreren Größen mit unterschiedlicher Detailtiefe zur Verfügung stehen, abhängig vom Gebrauch (in der Übersicht oder in der Einzeldarstellung) und dem Gerät des Anwenders bzw. der Datenverbindung.
- Wasserzeichen, das nicht stört:
-
In jedes Bild soll ein Wasserzeichen einmultipliziert werden, damit nicht Dritte angebliche Urheberrechte an den Bilder gelten machen können.
Programme und Abläufe
Die eigentliche Bildbearbeitung erfolgte mit dem Kommandozeilenprogramm
ImageMagick, das von
einem
Python-Script
gesteuert wird; d. h. das
Python-Script
liest Konfigurationsdateien
(meist *.json-Dateien)
ein und erstellt Programmaufrufe, die
ImageMagick
ausführt.
Screenshots erstellen und Beschneiden
Für jede „Mess- und Testsession“, in der Screenshots mit Oszillogrammen aufgezeichnet wurden, wird eine Art Dateiliste mit verschiedenen Parametern geschrieben. Diese müssen vom Anwender selbst gepflegt werden – hier müssen u. a. die Namen der Screenshot-Dateien wie auch die Koordinaten für das Ausschneiden der eigentlichen Oszillogramme eingetragen werden.
Auswahl von Parameter in der Bilderliste der Screenshots:
- Wunschgrößen für die kleineren Bilder
-
Wunschgrößen für die größeren, die kleineren und die Minibilder finden sich in den Parametern
grosz_wundgrosz_h,klein_wundklein_hsowiemini_wundmini_h. - Bereiche
_lissund_osc: -
Diese beiden Unterbereiche enthalten Screenshots für Oszillogramme oder Lissajous-Figuren, welche unterschiedlich bearbeitet werden müssen (unterschiedliche Koordinaten beim Ausschneiden aus dem Screenshot, unterschiedliche hereinmontierte senkrechte vs. waagerechte Linien). Jeder Bereich enthält:
- Parameter für das Ausschneiden:
-
Das sind die Parameter
xundy(Position der linken oberen Ecke des Ausschnittes) sowiewundh(Länge und Breite des Ausschnittes). - Koordinaten für einen „Orientierungsbalken“:
-
In den Oszillogrammen kann eine fette waagerechte Linie (Signal gleich null) und in die Lissajous-Figuren eine fette senkrechte Linie (Eingangssignal gleich null) eingezeichnet werden, die Parameter
rect_x1,rect_x2,rect_y1undrect_y2sind die Koordinaten eines einzuzeichnenden Rechtecks. - Wasserzeichendateien:
-
Die zugehörigen Wasserzeichendateien (die sich neben der Größe vor allem in der Farbe unterscheiden) werden in den Parametern
grosz_WM,klein_WMundmini_WMangegeben. - Bereich
files: -
Enthält eine Liste der zu verarbeitenden Screenshots.
Das eigentliche Beschneiden erfolgt dann durch ImageMagick – der letztendliche Befehlsstring könnte so aussehen (der Backslash steht für den hier eingefügten Zeilenumbruch) :
C:\…\magick.exe quelle.gif \ -crop 938x734+25+35 ausschnitt.gif
wobei ein Rechteck der Größe 938 mal 734 Pixel, dessen linke
obere Ecke bei den Koordinaten
[25 ; 35]
beginnt, ausgeschnitten wird.
Invertieren und nicht Farbinvertieren
Zum Verständnis dieses Programmschrittes ist ein kleiner Blick in Farbenlehre notwendig – das menschliche Auge besitzt, grob gesagt, (Farb)sehzelltypen mit drei verschiedenen Empfindlichkeiten; nämlich mit Empfindlichkeiten für Rot, für Grün und für Blau. Die anderen Farben werden zunächst über die Reizung mehrerer Farbsehzelltypen wahrgenommen – wenn wir beispielsweise Gelb sehen, werden zugleich die Zellen für Rot und Grün gereizt, die Wahrnehmung von weiß wiederum erfolgt nach Reizung aller verschiedenen Farbsehzelltypen.
Daraus ergibt sich im Groben eine Art Farbkreis zum Rechnen – Gelb kann, wie gesagt, als Addition von Rot und Grün verstanden werden, aber auch als Subtraktion von Weiß (Rot plus Grün plus Blau) abzüglich Blau. Gelb wird dadurch zu einer Art „Minus-Blau“ bzw. ist die Komplementärfarbe von Blau. Genauso wird Cyan zur Komplementärfarbe von Rot wie auch Magenta zur Komplementärfarbe von Grün:

Abb. 1: Prinzip des Farbkreises und der additiven und substraktiven Farbmischung.
Im Farbkreis bilden sowohl Rot, Grün und Blau (die Grundfarben der additiven Farbmischung – Mischfarben entstehen durch gemeinsames Aufhellen von Schwarz) als auch Cyan, Magenta und Gelb (die Grundfarben der subtraktiven Farbmischung – Mischfarben entstehen durch gemeinsames Abdunkeln von Weiß) jeweils ein Dreieck, wobei sich Rot und Cyan, Grün und Magenta sowie Blau und Gelb paarweise gegenüberliegen.
Wozu das Ganze? Es ging darum, einen Rechenvorgang zu finden (den ImageMagick ausführen kann), mit dem bei der Invertierung der Helligkeiten (schwarzer zu weißer Hintergrund) nicht auch noch die Farbe invertiert wird.
Ableitung des Verfahrens zu farbneutraleren Invertierung:
Zum Verständnis des vorgestellten Verfahrens ist es sinnvoll kurz zu erläutern, wie in einem Bildbearbeitungsprogramm wie ImageMagick eine in RGB definierte Farbe üblicherweise invertiert wird. Es wird für jeden Farbbestandteil (Rot, Grün oder Blau) nur der Wert von 100 % abzüglich des alten Wertes berechnet (In den folgenden Gleichungen steht P für ein Pixel sowie pR, pG und pB für die Rot-, Grün- und Blauwerte dieses Pixels; jeweils zwischen null und eins):
\( \begin{eqnarray} \left[ \begin{array}{c} p_{\textrm{neg,R}} \\ p_{\textrm{neg,G}} \\ p_{\textrm{neg,B}} \end{array} \right] & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} p_{\textrm{R}} \\ p_{\textrm{G}} \\ p_{\textrm{B}} \end{array} \right] \tag{1}\end{eqnarray} \)
Das heißt, aus einem „schwarzen“ Pixel würde ein weißes,
\( \begin{eqnarray} P_{\textrm{schwarz}} & = & \left[ \begin{array}{c} p_{\textrm{schwarz,R}} \\ p_{\textrm{schwarz,G}} \\ p_{\textrm{schwarz,B}} \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] \\~\\ P_{\textrm{schwarz,neg}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} p_{\textrm{schwarz,R}} \\ p_{\textrm{schwarz,G}} \\ p_{\textrm{schwarz,B}} \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] = P_{\textrm{weiß}} \tag{2}\end{eqnarray} \)
aus einem „weißen“ Pixel ein schwarzes und aus einem „reinroten“ Pixel (pR = 1 , pG = 0 , pB = 0) ein cyanfarbenes (pR = 0 , pG = 1 , pB = 1)
\( \begin{eqnarray} P_{\textrm{rot}} & = & \left[ \begin{array}{c} p_{\textrm{rot,R}} \\ p_{\textrm{rot,G}} \\ p_{\textrm{rot,B}} \end{array} \right] = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] \\~\\ P_{\textrm{rot,neg}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} p_{\textrm{rot,R}} \\ p_{\textrm{rot,G}} \\ p_{\textrm{rot,B}} \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right] = P_{\textrm{cyan}} \tag{3}\end{eqnarray} \)
sowie aus einem „knallgrünen“ Pixel (pR = 0 , pG = 1 , pB = 0) ein magentafarbenes (pR = 1 , pG = 0 , pB = 1)
\( \begin{eqnarray} P_{\textrm{grün}} & = & \left[ \begin{array}{c} p_{\textrm{grün,R}} \\ p_{\textrm{grün,G}} \\ p_{\textrm{grün,B}} \end{array} \right] = \left[ \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right] \\~\\ P_{\textrm{grün,neg}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} p_{\textrm{grün,R}} \\ p_{\textrm{grün,G}} \\ p_{\textrm{grün,B}} \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \right] = P_{\textrm{magenta}} \tag{4}\end{eqnarray} \)
Es wird also nicht nur Schwarz zu weiß, sondern auch jede „echte Farbe“ farbinvertiert, d. h. durch ihre Komplementärfarbe ersetzt. Wenn man jetzt eine derartige Farbinvertierung dadurch „verdoppelt“, man vor der eigentlichen Invertierung „180° am Farbkreis dreht“ (d. h. eine Farbinvertierung ohne Helligkeitsinvertierung vollzieht), könnten die ursprünglichen Farben erhalten bleiben.
Das kann, zumindest für die reinen additiven Grundfarben
(Rot, Grün, und Blau) dadurch erreicht
werden, dass sie in einer Vektormultiplikation des Farbvektors mit einem
speziellen Vektor durch ihre Komplementärfarben
(d. h. durch eine Mischung der jeweils anderen
beiden der drei additiven Grundfarben) ersetzt werden.
Das heißt, durch die Vektormultiplikation
wird Rot zu Cyan (Grün plus Blau),
Grün zu Magenta (Rot plus Blau) und
Blau zu Gelb (Rot plus Grün).
Und natürlich bleibt Schwarz
([0 0 0])
nach Multiplikation auch noch Schwarz.
Die Gesamtoperation (Invertieren ohne Farbinvertierung) sähe dann so aus:
\( \begin{eqnarray} P_{\textrm{neg,180°}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \cdot{} \left[ \begin{array}{c} p_{\textrm{R}} \\ p_{\textrm{G}} \\ p_{\textrm{B}} \end{array} \right] \tag{5}\end{eqnarray} \)
Ein schwarzes Pixel würde ein schwarzes Pixel bleiben,
\( \begin{eqnarray} P_{\textrm{schwarz,neg,180°}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \cdot{} \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] = \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] = P_{\textrm{weiß}} \tag{6}\end{eqnarray} \)
ein „knallgrünes“ Pixel bliebe ein „knallgrünes“ Pixel
\( \begin{eqnarray} P_{\textrm{grün,neg,180°}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \cdot{} \left[ \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right] = P_{\textrm{grün}} \tag{7}\end{eqnarray} \)
und ein „reinrotes“ Pixel ebenfalls ein „reinrotes“:
\( \begin{eqnarray} P_{\textrm{rot,neg,180°}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \cdot{} \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] = P_{\textrm{rot}} \tag{8}\end{eqnarray} \)
Für gesättigte Mischfarben wie Gelb (die Lissajous-Figuren im verwendeten Oszilloskop-Programm sind u. U. gelb) funktioniert das Verfahren aufgrund der „Übersteuerung“ eher nicht. Das liegt daran, dass ImageMagick nicht „übersteuerungsfest“ ist – Farbbestandteile unter null und über eins bzw. über 100 % existieren für das Programm nicht:
\( \begin{eqnarray} P_{\textrm{gelb,neg,180°}} & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \cdot{} \left[ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right] \\~\\ & = & \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 1 \\ 1 \\ 2 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ -1 \end{array} \right] \\~\\ & ≙ & \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] ≙ P_{\textrm{schwarz}} \tag{9}\end{eqnarray} \)
Das war oder ist aber aus Anwendungssicht kein großes Problem – die Lissajousfiguren, die (imScreenshot der Oszillogramm-Software) gelb auf schwarz sind, werden in der Invertierung nicht dunkelbraun, sondern schwarz und sind so noch von den grünen und roten Linien im Oszillogramm zu unterscheiden.
Nach dem grundlegenden Ansatz, wie die Screenshots
invertiert werden können, wurde noch herumprobiert und sowohl die
Farbrotationsmatrix als auch das Endergebnis skaliert –
die folgende
Gleichung 10
zeigt, was letztendlich im Script umgesetzt wurde.
(Der zweite Skalierungsvektor mit Faktor 1,2
kann in der oben beschriebenen Dateiliste für eine Serie von
Screenshots angepasst werden –
Parameter negColMatr.)
\( \begin{eqnarray} P_{\textrm{BG,wß}} & = & \left[ \begin{array}{c} 1{,}2 \\ 1{,}2 \\ 1{,}2 \end{array} \right] \cdot{} \left( \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] - \left[ \begin{array}{c} 0 \!&\! 1{,}5 \!&\! 1{,}5 \\ 1{,}5 \!&\! 0 \!&\! 1{,}5 \\ 1{,}5 \!&\! 1{,}5 \!&\! 0 \end{array} \right] \cdot{} P_{\textrm{BG,sw}} \right)\!\! \tag{10}\end{eqnarray} \)
Skalieren und „Fettrechnen“
Für die Präsentation der Oszillogramme in Bildertabellen werden kleine und trotzdem aussagekräftige „Bildchen“ der Oszillogramme gebraucht – die gewünschten Bildbreiten sind 462 Pixel für die mittlere Bildgröße und 318 Pixel für die Mini-Screenshots.
Da die Graphen in den Original-Screenshots (Bildbreiten z. Z. knapp 800 Pixel) sehr fein sind (Breite etwa 1 Pixel), ist beim Herunterskalieren damit zu rechnen, dass die Graphen bis zur Unkenntlichkeit verblassen. Deswegen erschien es sinnvoll, die Graphen vor dem Herunterskalieren zu verbreitern.
Da eine „richtige“ Faltung (Multiplikation jedes Pixels mit einer Fläche – z. B. in Form eines Pinselabdrucks) ziemlich rechenintensiv sein kann, wurde auf eine eher rustikale Art der Faltung zurückgegriffen, die RGB-Werte jedes Pixel werden den Farbwerten seiner vier Nachbarn (Pixel oben, rechts, unten und links) aufmultipliziert; was im Grunde genommen der Faltung mit einem einfachen Pixelkreuz entspricht.
Das wird realisiert, indem das eigentliche Oszillogramm fünfmal ausgeschnitten wird – einmal wie vorgesehen und noch weitere vier Mal mit jeweils einem Pixel Versatz in jede Richtung. Diese fünf Bilder werden nun Eines nach dem Anderen miteinander multipliziert. Danach sind die Graphen des Oszillogramms so breit, dass sich auch nach dem Herunterskalieren noch gut zu erkennen sind.
Für stärkeres Herunterskalieren wird das „Fettrechnen“ noch einmal gesteigert, jedes Pixel wird nicht nur mit seinen Nachbarpixeln, sondern auch mit denen, die zwei Pixel weit diagonal entfernt sind, multipliziert. So sind dann auch die sehr kleinen Vorschaubilder (mit Breite 318 Pixel) gut zu erkennen.
In Anschluss an das „Fettrechnen“ werden die Oszillogramme proportional auf die Bildbreiten 664 Pixel, 462 Pixel und 318 Pixel heruntergerechnet.
„Sourcesets“ und Bildertabellen
Soviel zur Bildaufbereitung, nun zu den Gründen für den Bedarf an unterschiedlich großen Bilder und Bildchen – und zu Sourcesets und Bildertabellen.
Zum einen werden die Oszillogramme in den Bildertabellen
als kleine Bildchen (hier 234 Pixel)
und groß für die Detailansicht gebraucht. Zum anderen bietet das
„Sourceset“-Attribut des
<img />-Tags
(zumindest im Firefox)
die Möglichkeit, dem
Browser mehrere Datei zum Download
und zur Darstellung vorzuschlagen, so dass dieser sich die
für die aktuelle Darstellungsgröße am besten geeignete Bilddatei
selbst aussuchen kann.
Dazu hier ein (verkürztes) Beispiel aus der Seite, zunächst nur der Ausschnitt mit der eigentlichen Einbindung der Bilddateien:
<a href="scrn/bild_grosz.gif" …> <img width="234" height="195" src="bild_klein.gif" srcset="bild_mini.gif 318w, bild_klein.gif 462w" /> </a>
Das <img />-Tag ist Teil eines Links,
mit dem der Anwender die Darstellung des großen Bildes
bild_grosz.gif erreichen kann.
Innerhalb des <img />-Tags, in dem
eine Bildgröße von 234 Pixel
(bei Darstellungsgröße 100 %)
vorgeschrieben wird, sollte der Browser
Bilddatei bild_mini.gif
(mit einer Breite von 318 Pixeln)
verwenden.
Stellt der Anwender die Darstellungsgröße jedoch auf beispielsweise
150 %, so muss der Browser das Bild mit
351 Pixeln Breite darstellen und kann in diesem
Sourceset auch die Bilddatei
bild_klein.gif (mit einer Breite
von 462 Pixeln) verwenden, denn die kleinere Bilddatei
bild_mini.gif (mit
Bildbreite 318 Pixeln) müsste der Browser schon hochskalieren.
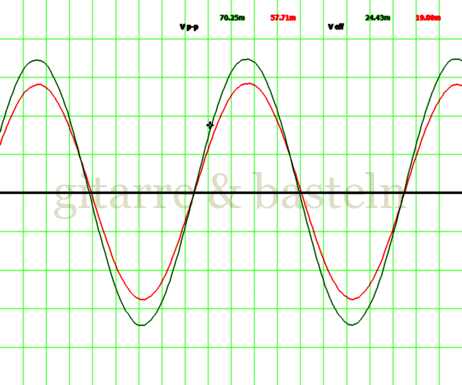
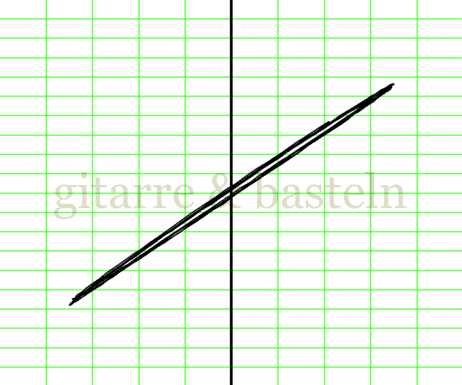
Soweit zum Sinn des Sourcesets; es folgt die Beschreibung der Anordnung in Bildertabellen. Um die Erläuterungen plausibler zu machen, wird hier ein kleiner Ausschnitt einer Bildertabelle als Beispiel eingebunden:
Bildertabelle 1: Signalverläufe und Lissajous-Figuren, aufgezeichnet im Eingangskreis von Messschaltung D1: (Zum Öffnen und Schließen hier klicken)
Zu sehen ist also in einem
<details>-Bereich
(der auf- und zugeklappt werden
kann):
-
Ein Tabellenkopf mit zwei Spaltentiteln,
-
Eine doppelte Tabellenzelle mit einer Überschrift über
-
zwei einzelne Tabellenzellen, jeweils mit einem Oszillogramm und ergänzenden Informationen darunter.
Die eigentliche Bildertabelle ist in einen
<details>-Tag
(man kann den Bereich durch Mausklick auf- und zuklappen)
eingeschlossen. Dieser Tag enthält eine
<summary> als Titelzeile:
<details class="bildertabellenrahmen" open="open"> <summary id="details_D1_2" class="TableCaption"> <span class="Title">Tabelle D1.2</span>: Signalverläufe … (<em>Zum Öffnen und Schließen … </em>) </summary> <!-- die eigentliche Bildertabelle … --> </details>
Für die eigentliche Bildertabelle wurde auf das Bootstrap-Frameworks zurückgegriffen – eine Konstruktion von Reihen gleichbreiter Rechtecke in einem Raster von zwölf gleichbreiten Feldern – es werden also in jeder Tabellenzeile zwei Tabellenzellen mit einer Breite von je sechs Rasterfeldern deklariert. Im Bildertabellenkopf sieht das so aus:
<div class="bildertabellenrahmen" id="bildtab_0815_D1_2"> <!-- Kopf Bildertabelle Tabellenzeile --> <div class="row"> <!-- Bildertabellenzelle links --> <div class="zweizellenheadline col0 col-sm-6 col-md-6 col-lg-6"> <strong>Oszillogramme <br /> Messschaltung D.1 – <br /> <em>u</em><sub>eing.</sub> und <em>u</em><sub>G</sub> </strong> </div> <!-- Bildertabellenzelle rechts --> … </div> </div>
Die Klasse „row“ setzt den Inhalt
des Divs in eine neue Box mit Satzspiegelbreite und
die Klassen „col-sm-6“,
„col-md-6“ und
„col-lg-6“
die enthaltenen Boxen (d. h.
Bildertabellenzellen) auf die Breite von sechs
Rasterfeldern, und zwar in Darstellungsmodus
„small“,
„medium“ und
„large“.
Soweit zum Kopf der Bildertabelle. Für jeweils zwei Oszilloskopen-Bilder (ein Oszillogramm und eine Lissajous-Figur) wird in der Bildertabelle eine Doppelzeile vorgesehen, wobei in der oberen Bildertabellenzeile Informationen enthalten sind, die beide Bilder in der unteren Bildertabellenzeile betreffen (im konkreten Fall die Eingangssignalspannung):
<div class="doublerow"> <!-- Doppelzelle Bilderueberschrift --> <div class="row"> <div class="col1 FullWdthTitle"> <strong>Eingangssignalspannung: <em>u</em><sub>eing.,eff</sub> = 24 mV </strong> </div> </div> <!-- Zwei Tabellenzellen mit Bildern --> <div class="row"> … </div> </div>
Die untere Bildertabellenzelle enthält, wie gesagt, die beiden Oszillogramme (als Minibilder wie als Links zu größeren Bildern) zuzüglich einiger Informationen:
<!-- Zwei Tabellenzellen mit Bildern --> <div class="row"> <!-- Bildertabellenzelle --> <div class="col1 col-sm-6 col-md-6 col-lg-6"> <!-- Link zum Großbild --> <a href="scrn/bild_grosz.gif" data-lightbox="SWscopescreenshots" data-title="Oszillogramm 1 von Tabelle D1.2 <br />u_{eing.} (grün): 10 mV / Div <br />u_G (rot): 10 mV / Div"> <!-- Dargestelltes Kleinbild --> <img width="234" height="195" src="scrn/bild_klein.gif" srcset="scrn/bild_mini.gif 318w, scrn/bild_klein.gif 462w" class="OsziTabMiniBild" alt="Oszillogramm" /> </a> <!-- Minicaption unter dem Bild --> <span class="minicaption"> <em>u</em><sub>eing.</sub> (<em>grün</em>): 10 mV / <span lang="en">Div</span>, <br /> <em>u</em><sub>G</sub> (<em>rot</em>): 10 mV / <span lang="en">Div</span> </span> </div> <!-- zweite Bildertabellenzelle --> … </div>
Im Link zum größeren Bild enthalten sind zwei Parameter, die vom
Javascript-Plugin Lightbox
genutzt werden – „data-lightbox“ und
„data-title“.
Lightbox stellt die angeklickten Bilder in einem
Popup groß dar und ermöglicht es, sich
vor- oder rückwärts zwischen den großen Bildern zu
bewegen.
Der Inhalt des Parameters „data-lightbox“
dient dabei als gemeinsames Label für mehrere Bilder, zwischen denen in der
vergrößerten Darstellung gewechselt werden kann, während
der Inhalt des Parameters „data-title“ die
Textinformationen unter die vergrößerten Darstellung des Bildes
platziert wird.
Die „Minicaption“ wiederum liegt in der Bildertabelle unter dem (kleinen) Bild.
Erstellen der Abbildungen
Kapitelinhalt:[ Überspringen ]- Größenvorgaben •
- Programmtechnische Umsetzung •
- Das Rasterproblem •
- Bildgestaltung •
- Arbeiten mit Gradationskurven
Größenvorgaben
Nach den in CSS-Bildertabellen zusammengefassten Oszillogrammen nun die „normalen“ Abbildungen und Illustrationen.
Worum geht es? Um die Aufbereitung von Grafiken, Schaltplänen, Diagrammen, die dem Browser in einem sogenannten Sourceset in mehreren Darstellungsgrößen zur Verfügung gestellt werden. Außerdem um die Möglichkeit, auf Satzspiegelbreite skalierte Abbildungen nach Anklicken in größerer Darstellung sehen zu können (Umsetzung über das Lightbox-Plugin).
Für die Breite der Bilder gab es dadurch mehrere Vorgaben:
960 Pixel als (ältere) Vorgabe für große Bilder (für eine Fensterbreite von mindestens 1024 Pixel),
318 Pixel als kleinste Vorgabe für kleine Telefone (mit 320 Pixel) Fensterbreite,
-
Eine Bildbreite, die mehrere zehn Prozent größer ist als der Satzspiegel, damit der Browser beim Herunterskalieren / Anpassen der Bildbreite noch etwas „Luft“ hat. Bei einer Satzspiegelbreite von 36 em und einer Standardschriftgröße von 14 px ergibt sich hier eine Bildbreite zwischen 600 px und 700 px.
Daraus ergeben sich – bei einer geometrischen Reihe – vier sinnvolle Bildbreiten:
- Breite 318 Pixel – Suffix „
_mini“ -
Für kleine Bilder auf kleinen Telefonen,
- Breite 460 Pixel – Suffix „
_klein“ -
Zwischenbreite, 45 % Prozent breiter als „
_mini“; - Breite 664 Pixel – Suffix „
_mitte“ -
Zwischenbreite, 45 % Prozent breiter als „
_klein“; - Breite 700 Pixel – Suffix ebenfalls „
_mitte“ -
Für Datenblattauszüge,
- Breite 960 Pixel – Suffix „
_grosz“ -
Standardbreite, 45 % Prozent breiter als „
_mitte“. Für die in der Bildansicht verlinkten großen Bilder, sowie
Später kamen noch zwei weitere Größen dazu:
- Breite 192 Pixel – Suffix „
_icon“ -
Für die Teaserbildchen; z. B. in der
index.html - Breite größer als 960 Pixel – Suffix „
_riesig“ -
Für Bilder, die größer als 960 Pixel sein müssen, weil sonst Details verlorengingen.
Die vier erstgenannten Größen werden Firefox im
Sourceset-Attribut des
<img />-Tags
angeboten, so dass sich der Browser die kleinste passende Bilddatei
für die berechnete Bilderbreite aussuchen kann:
<img alt="EXCEL-Diagramm" width="480" height="310" src="bilder/GIFbild_244_grosz.gif" srcset="bilder/GIFbild_244_mini.gif 318w, bilder/GIFbild_244_klein.gif 460w, bilder/GIFbild_244_mitte.gif 664w, bilder/GIFbild_244_grosz.gif 960w" title="Zum Vergrößern klicken" />
Für JPEG-komprimierte Bilder wurde die Zahl der unterschiedlichen Auflösungen kleiner gehalten – hier sind kleinere Bilder nicht unbedingt kleinere Dateien, so dass es auch nicht sinnvoll ist, jede Bildbreite anzubieten.
Programmtechnische Umsetzung
Die unterschiedlichen Bildgrößen werden auch hier über ein
Python-Script,
das dann
ImageMagick
aufruft, erzeugt.
Dabei werden außerdem noch Wasserzeichen einmultipliziert.
Die Beschreibung der unterschiedlichen Wasserzeichen, -größen und -farben
findet sich
weiter unten.
Das Python-Script
wird im Wesentlichen über zwei Konfigurationsdateien gesteuert –
eine Liste aller Bilder
(__bilderliste.json) sowie
eine Konfigurationsdatei
__bildersettings.json.
In der Datei
(__bilderliste.json) –
eine große Tabelle, werden die Einstellungen für jede Quellbilddatei hinterlegt
(im Folgenden die Spalten / Einstellungen für eine Datei):
{"job": "skal" /* Skalieren|Kopieren */
,"wm": "STD" /* Welches Wasserzeichen */
,"transpFrom": "grayF4" /* Hintergr. Quellbild */
,"transpTo": "grayF4" /* Transparenz Zielbild */
,"sz": "grosz" /* Groesze Quellbild */
,"minSz": "mini" /* Runterskalieren bis */
,"name": "r-dose_schem"
,"ext": "gif"
,"w": 960
,"h": 282 }
Der Parameter „sz“ dient auch als
Dateinamensuffix für die Quellbilddatei; er muss mit
Unterstrich an den eigentlichen Dateinamen angehängt werden.
In der Konfigurationsdatei __bildersettings.json werden
verschiedene Einstellungen festgelegt, zunächst die Einstellungen für die zu
erstellenden Sourceset-Bilder – jeweils
für
*.gif- und
*.jpg-Dateien:
… "srcset": {"jpg": {"icon" :["icon","" ,"" ,"" ,"" ,""] ,"mini" :["" ,"mini","" ,"" ,"" ,""] ,"klein" :["" ,"" ,"klein","" ,"" ,""] ,"mitte" :["" ,"mini","" ,"mitte","" ,""] ,"grosz" :["" ,"" ,"klein","" ,"grosz",""] ,"riesig":["" ,"" ,"klein","" ,"grosz",""] } , "gif": {"icon" :["icon","" ,"" ,"" ,"" ,""] ,"mini" :["" ,"mini","" ,"" ,"" ,""] ,"klein" :["" ,"mini","klein","" ,"" ,""] ,"mitte" :["" ,"mini","klein","mitte","" ,""] ,"grosz" :["" ,"mini","klein","mitte","grosz",""] ,"riesig":["" ,"mini","klein","mitte","grosz",""] }" }
Abgesehen davon, dass
„icon“-Dateien
weder herunterskaliert noch erstellt werden, reichen im Falle von
„*.jpg“-Dateien
zwei Größen für das Sourceset aus.
„riesig“-Dateien werden
immer herunterskaliert und sind nie im
Sourceset enthalten.
Im Abschnitt downscaleSrc wird festgelegt,
welche Bildgrößen aus welchen Bildgrößen berechnet werden:
… "downscaleSrc": {"jpg": {"icon" :["","","","mitte","grosz","riesig"] ,"mini" :["","","","mitte","grosz","riesig"] ,"klein" :["","","","" ,"grosz","riesig"] ,"mitte" :["","","","" ,"grosz","riesig"] ,"grosz" :["","","","" ,"" ,"riesig"] ,"riesig":["","","","" ,"" ,"" ] } ,"gif": {"icon" :["","mini","klein","mitte","" ,"" ] ,"mini" :["","" ,"klein","mitte","" ,"" ] ,"klein" :["","" , "" ,"mitte","grosz","" ] ,"mitte" :["","" , "" ,"" ,"grosz","riesig"] ,"grosz" :["","" , "" ,"" ,"" ,"riesig"] ,"riesig":["","" , "" ,"" ,"" ,"riesig"] } }
So müssen die „*.jpg“-Dateien,
die weiter herunterskaliert werden,
eine Mindestgröße „mitte“ haben,
während „*.gif“-Dateien nur aus
den ein oder zwei Stufen größeren Bilddateien herunterskaliert werden können
(das dieser Vorgabe zugrundeliegende
„Rasterproblem“ wird
im nächsten Abschnitt
beschrieben).
In der Konfigurationsdatei __bildersettings.json
werden außerdem noch grundsätzlichen Einstellungen
(Namen, Größen und Reihenfolge der verschiedenen
Größenmodi und der Wasserzeichen, Grauwerte der
Transparenzfarben etc.) hinterlegt.
Das Rasterproblem
Kapitelinhalt:[ Überspringen ]Das Problem an sich
Einige Schaltpläne und Skizzen wurde in einem
Vektorzeichenprogramm
(CorelDRAW)
gezeichnet oder aufgearbeitet und anschließend in ein Pixelbild
(*.gif)
exportiert. Die dabei entstandenen Bilddateien waren nicht besonders
schön – wie mit einem zerfaserten, manchmal halbleeren Filzstift
gezeichnet
(siehe dazu auch im Folgenden
Abbildung 2 und
Abbildung 3).
Das Problem verlangt nach einer Erläuterung anhand einer Beispieldatei. Der obige Schaltplan (eine etwas eigenwillige Interpretation der Box of Rock) ist in CorelDRAW als Bilddatei einschließlich des weißen Hintergrundes 195 mm breit und 70 mm hoch (entspricht einem Format von 7,68 × 2,75 Zoll bzw. 553 × 198 Punkten), die Schriftgröße ist gleich 10 Punkte und die Linienbreite gleich einem Punkt.

Abb. 2: Schaltplan, direkt aus CorelDRAW etwa auf die Darstellungsbreite von 460 Pixel (Auflösung 60 dpi) gerastert.
Das Bild wurde auf eine Größe von 460 × 165 Pixeln gerastert. Dabei wird quasi ein Raster bzw. ein Netz von 460 × 165 Maschen über das Bild gelegt und für jede Masche die durchschnittliche Helligkeit ermittelt. Dabei sind die wenigen Maschen sehr groß bzw. die Details des Bildes recht klein gegenüber dem Raster der Maschen – die Großbuchstaben der Schrift von Schriftgröße 10 pt (Großbuchstaben mit 70 % der Schriftgröße) wären dann etwa sechs Pixel bzw. Maschen hoch (10 pt ⋅ 70 % ⋅ 460 px / 553 pt), die Strichbreite läge bei weniger als 1 Pixel bzw. 1 Masche (1 pt ⋅ 460 px / 553 pt). Diese Art der Darstellung ist zwangsläufig schlecht, wie ein Blick auf die beiden Bilder in Abbildung 3 beweist:

Abb. 3: Detail aus obiger Abbildung 2 (in Schwarzweiß) – links das Originalbild mit voraussichtlichen Rasterkanten, rechts die Rasterung auf 60 dpi.
Hier sind die Probleme der groben Rasterung schon zu erkennen:
- Schriftgröße:
-
Die Buchstaben sind mit etwa sechs Pixeln Versalhöhe gerade so lesbar – Kleinbuchstaben oder Indizes wären es nicht mehr.
- Linien:
-
Die Abstände der Rasterlinien korrelieren nicht mit den Abständen der Linien in der Zeichnung; manchmal sind liegen Linien / Verbindungen der ursprünglichen Zeichnung genau auf dem Raster (dann sind auch die gerasterten Linien / Verbindungen klar und schwarz, wie z. B. über bzw. unter dem Potentiometer), manchmal liegen die Linien / Verbindungen genau zwischen zwei „Rastermaschen“, und man sieht anstelle einer klaren schwarzen Linie eine verwaschene graue.
- Details:
-
Die beiden Kondensatoren C7 und C8 bspw. sind kaum mehr als ein verschmierter Klumpen. Das heißt, wenn die Details zu fein sind (z. B. der Abstand der Kondensatorplatten nicht deutlich größer als das Raster), gehen sie beim Rastern verloren.
Lösungsversuche – Höherrastern und Skalieren
Der grundlegende Ansatz besteht nun darin, die Vektorgrafik in einer wesentlich höheren Auflösung zu rastern (hier mit 600 ppi) und dieses Pixelbild dann auf unterschiedlichen Weg „kleinzurechnen“. Dabei wurden mehrere Ansätze verfolgt:
- Direkt herunterskalieren:
-
Das Bild wurde aus CorelDRAW mit 600 ppi (Bildbreite 4606 Pixel) exportiert und in einem Schritt von Bildbreite 4606 Pixel auf Bildbreite 960 Pixel (etwa 20,8 %) heruntergerechnet.
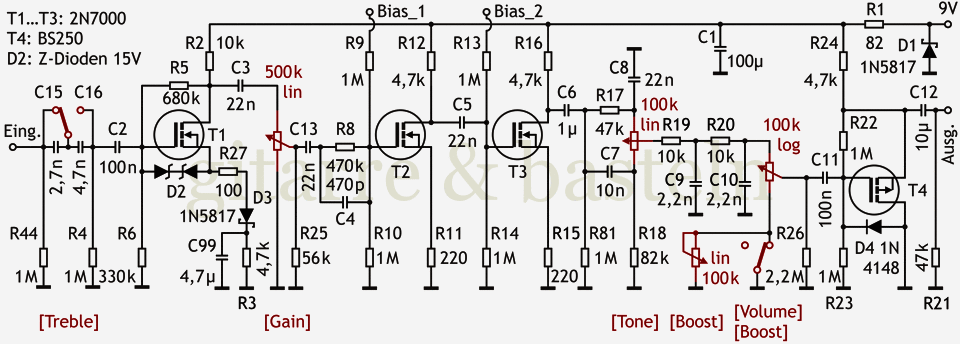
Abb. 4: Schaltplan nach Export in Bilddatei 600 dpi und direktem Herunterrastern in einem Schritt (von 4606 px auf 960 px).
Hier ist natürlich mit vergleichbaren Problemen wie bei oben beschriebenen direkten Rastern zu rechnen – die Position des Details entscheidet mit über dessen Darstellung. In der folgenden Abbildung 5 rechts zeigt sich das in der unterschiedlichen Darstellung der beiden Kondensatoren C7 und C8.
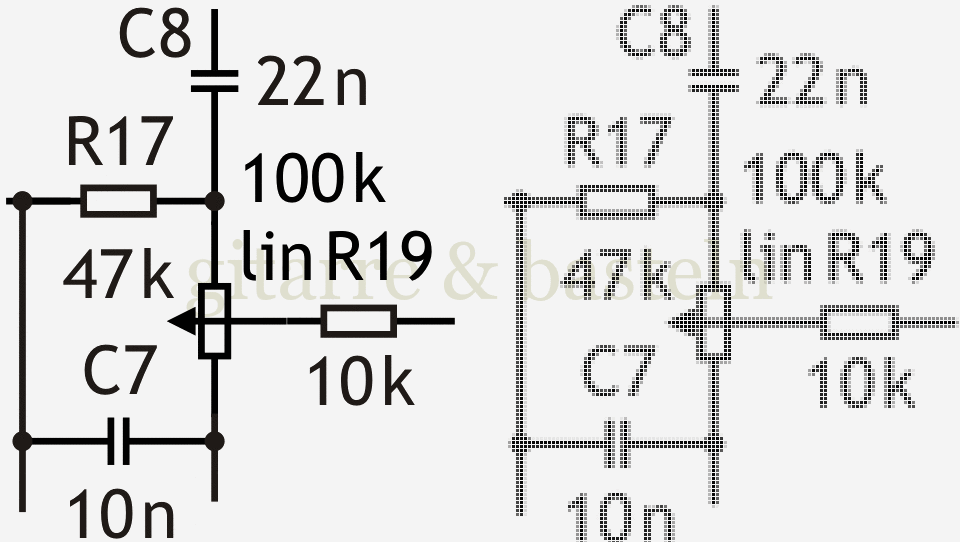
Abb. 5: Detail aus obiger Abbildung 4 (in Schwarzweiß) – links in etwa das Originalbild, rechts das Ergebnis von Rastern und Skalieren.
- In kleinen Schritten herunterskalieren:
-
Im nächsten Versuch / Ansatz wurde das in hoher Auflösung gerasterte Bild in sehr kleinen Schritten heruntergerechnet (acht Durchläufe, bei denen das Bild jeweils auf etwa 82 % verkleinert wurde).
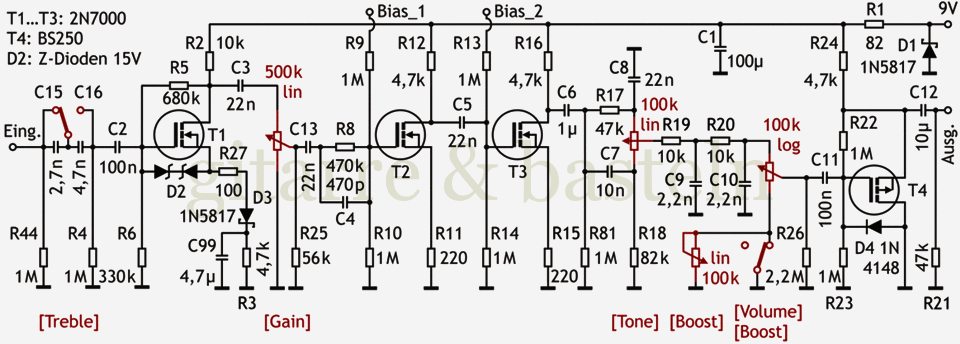
Abb. 6: Schaltplan nach Export in Bilddatei 600 dpi und schrittweisem Herunterrastern (von 4606 px auf 960 px in acht Schritten auf jeweils etwa 82 % verkleinert).
Die Darstellung insbesondere der beiden Kondensatoren wirkt etwas ausgeglichener, wenngleich alle Linien ein grauer Saum umgibt, eine Folge der häufigen Neuberechnung des Bildes. Es entsteht eine Art Patina, die an ältere Fachbücher (mit billigem Papier) erinnert.
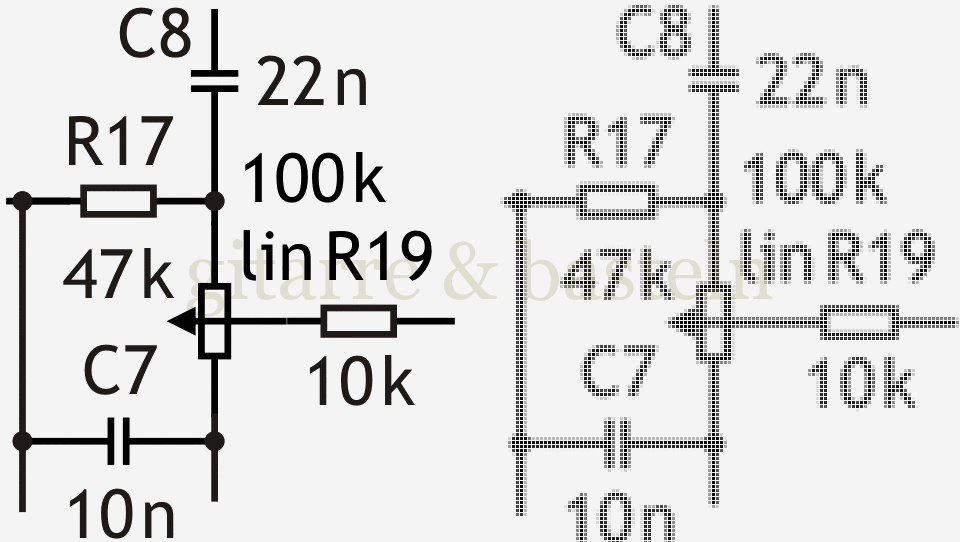
Abb. 7: Detail aus obiger Abbildung 6 (in Schwarzweiß) – links das Originalbild, rechts die Rasterung in kleinen Schritten.
- Im goldenen Schnitt herunterskalieren:
-
Im letzten Versuch wurde die in hoher Auflösung gerasterte Zeichnung in mehreren Schritten kleiner gerechnet, wobei alle Schritte bis auf den ersten das Bild im Verhältnis des goldenen Schnittes (hier abwechselnd auf 61 % bzw. 62 %; ansonsten ist der Goldene Schnitt gleich √1,25 ±0,5 ≈ 0,618).
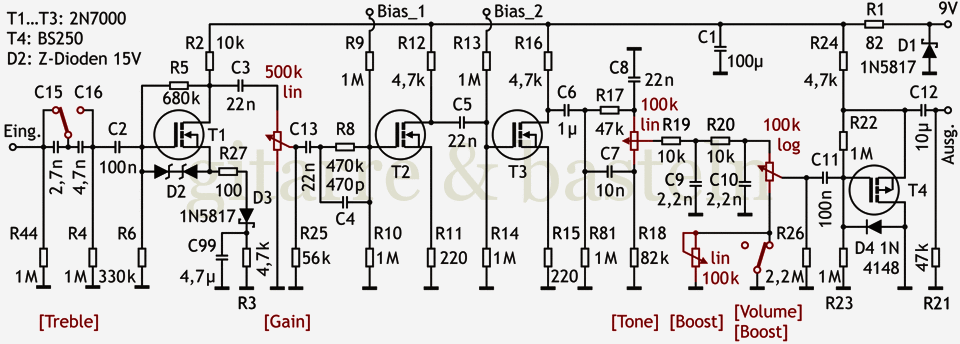
Abb. 8: Schaltplan nach Export in Bilddatei 600 dpi und schrittweisem Herunterrastern (von 4606 px auf 960 px in Schritten zu 61 % bzw. 62 % alternierend).
Auch wenn die Unterschiede minimal sind, scheint das der sinnvollste Ansatz zu sein:
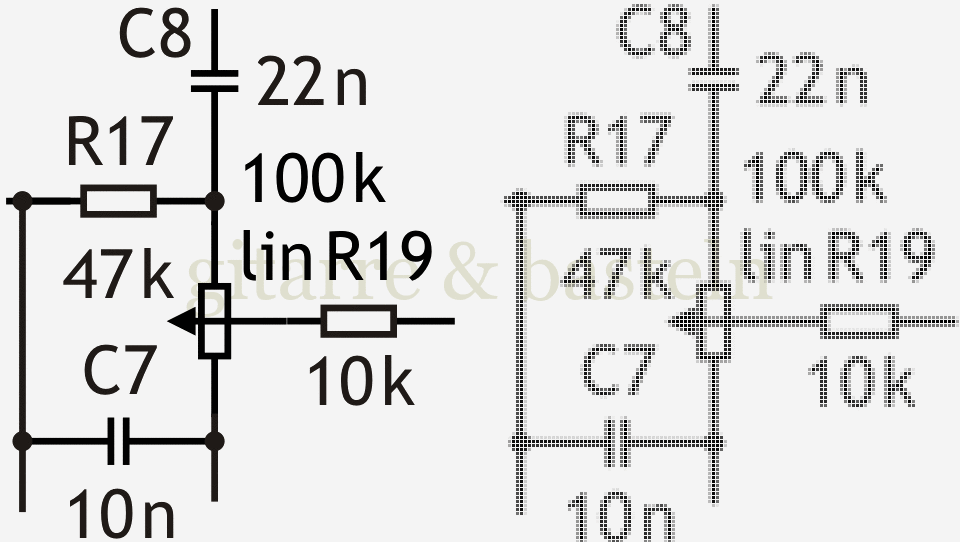
Abb. 9: Detail aus obiger Abbildung 8 (in Schwarzweiß) – links in etwa das Originalbild, rechts das Ergebnis von Rastern und Skalieren im goldenen Schnitt.
Bildgestaltung
Aus dem oben beschriebenen Problem des Aufrasterns ergeben sich natürlich auch bestimmte Anforderungen in den Zeichnungen wie z. B. Mindestschriftgrößen und Mindestlinienstärken in den Zeichnungen.
Die Lösung des Autors für dieses Problem ist hochgradig unspektakulär – Dreisatz und EXCEL. Das heißt, anhand sinnvoller Vorgaben (bei einem aufgerasterten, 480 Pixel breit dargestellten Bild sollten die Schriften mindestens acht Pixel groß und die Linien etwa ein bis eineinhalb Pixel breit sein) lassen sich für Zeichnungen gegebener Breite angemessenen Werte für Schriftgröße und Liniendicke berechnen.
Übernahme der Schaltpläne aus PSPICE
Kapitelinhalt:[ Überspringen ]In einem Blog zum Thema Gitarenelektronik sind natürlich auch Schaltpläne enthalten. Der Autor hat dabei sehr lange mit einer Studentenversion des Programms PSPICE gearbeitet – sei es, um Schaltungen zu simulieren, sei es, um sie einfach nur zu zeichnen, und die Schaltungen dann in die Artikel übernommen.
Allerdings wurde bei der Übernahme der Schaltpläne aus PSPICE über die Jahre kräftig „abgespeckt“ – anstelle eines Exports über das AutoCAD-Format in CorelDRAW und einem umständlichen Neubau der Bilder (Linien und Schriften müssen in CorelDRAW in unterschiedliche Ebenen sortiert werden, um den Linien sinnvolle Linienstärken und den Schriften keine Linienstärken zuzuweisen) mit anschließenden Rastern wurden die Displayeinstellungen in PSPICE so geändert (größere Schrift in passender Schriftart, fettere Linien, ausschließlich Schwarzweiß), dass sich auch aus den Screenshots verwendbare Illustrationen erstellen lassen.
Herunterskalieren der Screenshots
Diese Screenshots müssen allerdings noch für die Verwendung auf der Seite optimiert (zugeschnitten und skaliert) werden. Auch hier wurden mehrere Ansätze des Kleinrechnens der Bilder ausprobiert:
- Direkt herunterskalieren:
-
Der Schaltplan wurde in PSPICE etwa auf Bildschirmbreite (Bildschirmauflösung 1280 × 1024) vergrößert und als Screenshot gespeichert und zugeschnitten (Programmmenüs, Scrollbalken und breite weiße Ränder wurden entfernt). Das zwischen 1000 Pixel und 1200 Pixel breite Bild wurde anschließend in einem Schritt auf Bildbreite 960 Pixel heruntergerechnet.
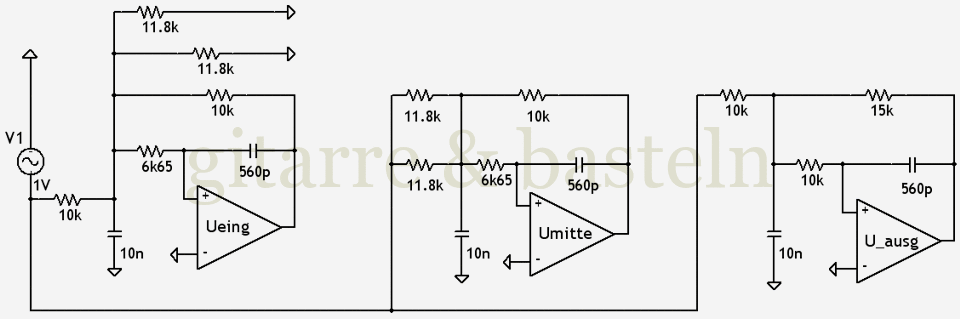
Abb. 10: Schaltplan, direkt aus PSPICE auf die große Bildbreite von 960 Pixel gerastert.
An einigen unschönen Details (stufiger Kreis bei der Eingangsspannungsquelle, stufige Außenkanten bei den Operationsverstärkern) ist schon hier zu erkennen, dass diese Methode des Kleinrechnens nicht optimal ist.
- In kleinen Schritten herunterskalieren:
-
Im nächsten Versuch / Ansatz wurde der zugeschnittene Screenshot vergrößert (die Pixelzahl verdoppelt) und das Bild dann in sehr kleinen Schritten auf die Breite von 960 Pixel heruntergerechnet (sechs Durchläufe, bei denen das Bild jeweils auf etwa 86 % bis 87 % verkleinert wurde).
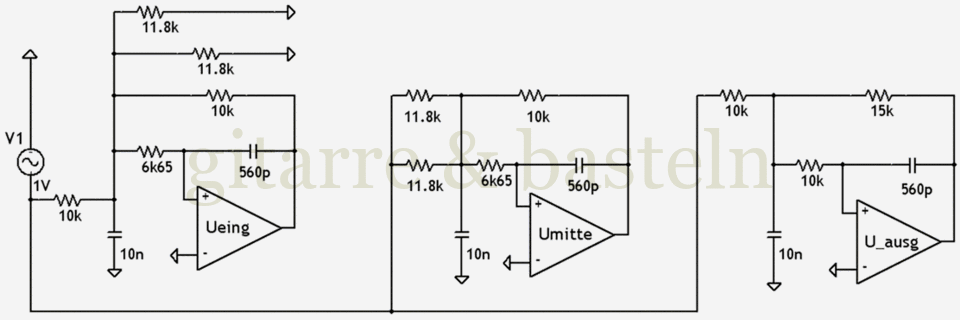
Abb. 11: Schaltplan, direkt aus PSPICE auf die große Bildbreite von 960 Pixel gerastert.
Das sieht schon besser aus, auch wenn die Details (zum Beispiel die Schrift) einen leichten Saum haben.
- Im goldenen Schnitt herunterskalieren:
-
Im letzten Versuch wurde zugeschnittene Screenshot zuerst mit ganzzahligem Vergrößerungsfaktor auf eine Breite von deutlich über viertausend Pixel hochskaliert (z. B. auf die vierfache Breite) und anschließend einer vorher berechneten Reihe von Größen (4066 Pixel, 2513 Pixel und 1553 Pixel auf 960 Pixel) folgend mehrmals im Verhältnis des goldenen Schnitts herunterskaliert.
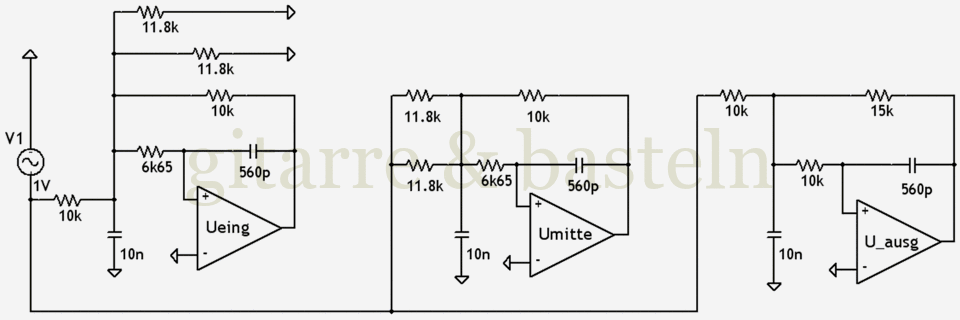
Abb. 12: Schaltplan, direkt aus PSPICE auf die große Bildbreite von 960 Pixel gerastert.
Sofern das hier überhaupt genau erkennbar ist, scheint dieser Weg der mit der brauchbarsten Darstellungsqualität zu sein.
Korrekturen und Ergänzungen
Soweit das Groß- und Kleinrechnen von fertig erstellten Schaltplänen. Allerdings sind bei diesen Schaltplänen hin und wieder auch Korrekturen und Ergänzungen notwendig – sei es, dass beim Zeichnen Fehler gemacht wurden, sei es, dass Bauelemente ergänzt oder modifiziert werden müssen (Schalter, Lautsprecher). Außerdem können Modifikationen notwendig sein (farbliche Hintergründe, Schrift in anderen Farben).
Zeichnungs- und Schriftkorrekturen erfolgen am besten vor dem Kleinrechnen / Neurastern, damit die Unterschiede durch das mehrmalige Neurastern ein wenig abgeschliffen werden und so weniger auffallen. Farbänderungen (zumindest flächige Umfärbungen) sollten danach erfolgen, da sonst an Linien über Farbkanten hässliche Unschärfen entstehen.
Schließlich ist es sinnvoll darauf zu achten, dass die Hintergründe der Vorlagen vor dem Herunterskalieren immer weiß sind – ansonsten können es beim Herunterskalieren insbesondere an Kanten hässliche Artefakte („Überschwingen“) entstehen – direkt an der herunterskalierten Kante ist der Kontrast erhöht und der Hintergrund noch heller als sonst.
Arbeiten mit Gradationskurven
Kapitelinhalt:[ Überspringen ]Zu den wichtigsten Werkzeugen in der Bildbearbeitung gehören Gradationskurven. In ihnen ist ein Zusammenhang zwischen der Helligkeit eines Bildes (oder einer Teilfarbe eines Bildes wie z. B. Rot, Grün oder Blau) vor und nach der Behandlung mit der Gradationskurve. Verständlicher ist das möglicherweise an einem Beispiel:
Seitenhintergrund für Bilder
Im Grunddesign der Seite wurde als
Hintergrundfarbe ein helles Grau
(#f4f4f4
bzw. [244 , 244 , 244]
oder 95 % weiß)
festgelegt.
Alle „Strichzeichnungen“
(Schaltpläne, Skizzen, Diagramme)
sollten weitestgehend diese Hintergrundfarbe haben.
Der einfachste Weg, das bei einer Schwarz-weiß-Grafik zu erreichen, ist das
Abdunkeln der gesamten Grafik auf etwa 95 % weiß
(genaugenommen auf 244 von maximal 255).
Im folgenden Diagramm in
Abbildung 13
entspricht der braune Graph mit dem Label
website_244 diesem Vorgehen –
jeder Helligkeit im Ausgangsbild wird eine etwa 5 % geringere
Helligkeit im Ergebnisbild zugeordnet.
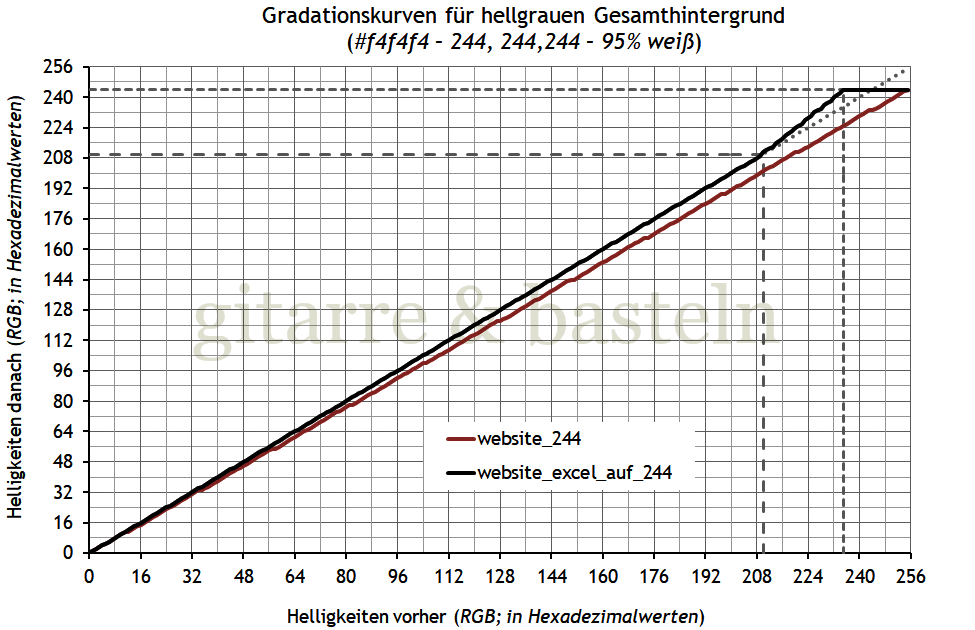
Abb. 13:
Gradationskurven, um den Hintergrund einer schwarz-weißen Zeichnung
auf einen bestimmten Grauwert
(Farbdefinition #f4f4f4)
zu setzen – entweder durch kontinuierliches Abdunkeln
(brauner Graph) oder durch Abdunkeln
nur der hellen Bereiche
(schwarzer Graph).
Allerdings hatte der Autor zu Beginn des Blogs einigen
EXCEL-Diagrammen diese Hintergrundfarbe
#f4f4f4 schon bei der
Grafikerstellung in EXCEL zugewiesen,
wobei
EXCEL diese Hintergrundfarbe nicht unbedingt
getroffen hat.
Hier wäre also Nachdunkeln keine Option gewesen, außerdem sollten die Fehler
von EXCEL korrigiert werden.
Daraus leitete sich die zweite Gradationskurve in obigem Diagramm
ab:
-
Helles Grau von zwischen 92 % und 100 % wird auf die gewünschte Hintergrundfarbe von 95 % bzw.
#f4f4f4festgesetzt (oberer ebener Abschnitt der schwarzen Gradationskurve). -
Grau zwischen 82 % bis 92 % wird so leicht im Kontrast verstärkt, dass es sich im Ergebnisbild zwischen 82 % bis 95 % bewegt (oberer, steilerer Abschnitt der schwarzen Gradationskurve).
-
Dunklere Farben (dunkler als 82 % weiß) werden nicht verändert (Hauptteil der schwarzen Gradationskurve).
Schriftfarbe Schwarz zu Rot
Nun zu etwas weniger technischen Basteleien, dazu mit den Gradationskurven für die einzelnen Farben:
Zunächst war es gewünscht, einige Schriftzeichen bzw. Teile einer Strichzeichnung von Schwarz auf Weinrot umzufärben. Das heißt, weiß sollte weiß bleiben und schwarz zu weinrot bzw. dunkelrot geändert werden. Dazu wurde der entsprechende Teil des Bildes maskiert. Anschließend wurden die in folgender Abbildung 3 dargestellte Gradationskurven angewendet:

Abb. 14:
Gradationskurve, um bei einem schwarz-weißen
Screenshot Schrift als Weinrot
(Farbdefinition #71ffff)
hervorzuheben.
Es zeigt sich, dass (im maskierten Bereich)
die Helligkeiten von Grün und Blau nicht verändert werden –
für Grün und Blau läuft der Graph gerade von
[0 , 0]
bis
[256 , 256].
Anders für Rot, hier ist der dunkelste Wert für das Ergebnisbild
113, so dass dort die Farbe Schwarz
#000000 durch
ein Weinrot #71ffff ersetzt wird. Dazu kommt, dass auch
die Grautöne immer mehr Rot als Grün und Blau enthalten, also graue Ränder bzw.
Übergänge von Schwarz auf Weiß auch umgefärbt werden.
Gelber Hintergrund
Nun quasi das Gegenteil des eben beschriebenen – das Auffüllen bzw. Abdunkeln eines Hintergrundes in einer bestimmten Farbe. Das kann, z. B. in einem großen Schaltplan, sinnvoll sein, um bestimmte Teile des Plans (wie verschiedene Baugruppen) zu kennzeichnen. Siehe dazu das folgende Diagramm (Abbildung 15):
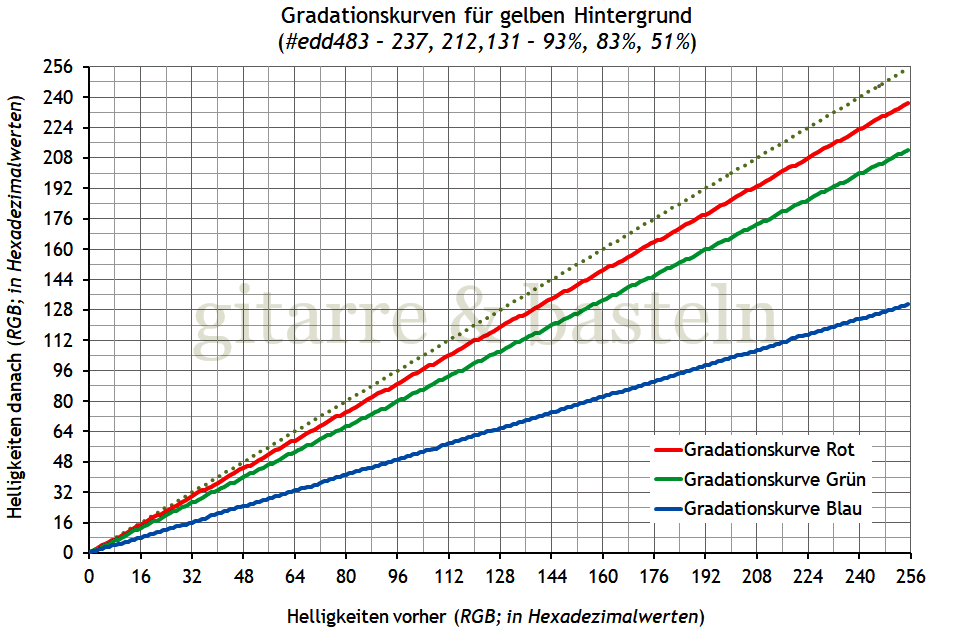
Abb. 15:
Gradationskurve, um den Hintergrund eines Ausschnitts in einem
schwarz-weißen Screenshot gelb
(Farbdefinition #edd483)
umzufärben.
Die Gradationskurven für alle drei Farben
Rot, Grün und Blau beginnen im (schwarzen) Nullpunkt
und laufen zu verschiedenen Maximalwerten –
237 von 255 für Rot,
212 von 255 für Grün und
131 von 255 für Blau, was einem Farbton
#edd483 bzw. (ungefähr) einem warmen Gelb oder einem dezenten
„Goldocker“ entspricht.
Das heißt, im so behandelten Teil eines Schwarz-Weiß-Bildes werden die
einzelnen Farbwerte der Hintergrundfarbe als Maximalfarben in die drei
Gradationskurven eingetragen und so die vorherige Hintergrundfarbe
Weiß durch die neue Hintergrundfarbe (in diesem Falle Gelb)
und der Schwarz-Weiß-Übergang durch einen
Übergang von Schwarz zur neuen Hintergrundfarbe ersetzt.
Es empfiehlt sich, derartige Umfärbungen als letzten Schritt der Bildbearbeitung (nach dem Skalieren / Neurechnen der Bilder) durchzuführen.
Verwendung von Wasserzeichen
Die Wasserzeichen lassen sich kurz abhandeln – für die gesamte Seite werden Bilddateien, sofern es sich nicht um geistiges Eigentum Dritter handelt bzw. in ihnen geistiges Eigentum Dritter dargestellt wird, mit dem Motto / Label der Seite „gitarre & basteln“ versehen. Geistiges Eigentum Dritter wird entweder nicht (inhaltlich) verändert oder mit einem roten Wasserzeichen / Warnhinweis „Private use only!“ versehen.
Technisch gesehen handelt es sich bei den Wasserzeichen um RGB-Bilddateien mit weißem Hintergrund (d. h. im Hintergrund des Wasserzeichens sind alle drei Farbwerte gleich 100 % bzw. eins), die horizontal und vertikal zentriert in das Bild einmultipliziert werden.
Der Name jeder Wasserzeichendatei enthält Hinweise auf die Größe des Bildes, in das es einmultipliziert werden kann, und auf die Farbe – letztere abhängig vom Einsatzzweck:
- Unterschiedliche Stempelgrößen:
-
-
„
huge“: Größe 840 × 280 Pixel; Schriftgröße 112 Punkte; für große Bilder (960 Pixel breit) -
ohne Größenlabel: 600 × 200 Pixel; Schriftgröße 80 Punkte; für Datenblatt-Faksimile (700 Pixel breit)
-
„
medi“: 450 × 150 Pixel; Schriftgröße 60 Punkte; für mittelgroße Bilder (664 Pixel breit) -
„
mini“: 360 × 120 Pixel; Schriftgröße 48 Punkte; für kleine Bilder (462 Pixel breit) -
„
tiny“: 225 × 75 Pixel; Schriftgröße 30 Punkte für sehr kleine Bilder (319 Pixel breit)
-
- Unterschiedliche Schriftfarben (und Texte):
-
-
Ohne Farblabel – Farbe:
#dededd(Dezimal: 222, 222, 200): Standardfarbe. Text: „gitarre & basteln“ -
Label „
blk“: Farbe: „black“; Text: „gitarre & basteln“; für Schwarzweißfotos. -
Label „
red“: Farbe: „brown“ (gemeint ist ein dunkles Weinrot); Text: „gitarre & basteln“; für Fotos. -
Label „
grau“: Farbe:#979797(Dezimal: 151, 151, 151); Text: „gitarre & basteln“; Für dunkle Skizzen, um nicht übersehen zu werden. -
Label „
lgt“: Farbe:#e9e9d8(Dezimal: 233, 233, 216) Text: „gitarre & basteln“ Für helle und / oder filigrane Diagramme, um nicht zu stören. -
Label „
XXX“: Farbe: „red“; Für Warnhinweis; z. B. „For private use only!“ (d. h. der dargestellte Inhalt darf nicht kommerziell weiterverwendet werden).
-
Alle Wasserzeichen wurden mit ImageMagick, gesteuert über ein Batch-Skript, vorproduziert und als Bitmaps in einem gemeinsamen Verzeichnis abgelegt.