Ein fettes Lama – Teil II
Das sezierte Lama
Kapitelinhalt:[ Überspringen ]- High und Low •
- CMOS als Verzerrer •
- Der Arbeitspunkt •
- Gegenkopplung und Verstärkung •
- Der Eingangswiderstand •
- Betriebsspannung und Kennlinie •
- Der Frequenzgang •
- Literatur
Nachdem die Schaltung des Verzerrers kurz vorgestellt und die Änderungen im Vergleich zum Red Llama erläutert wurden, sollen im Folgenden die theoretischen Grundlagen dargestellt werden. Dabei wird zunächst von der Schaltung des originalen Red Llama ausgegangen (Kennlinien, Arbeitspunkte, Betriebsspannung). Die Theorie von Eingangswiderstand und Frequenzgang wird an der Schaltung des realisierten Verzerrers erklärt.
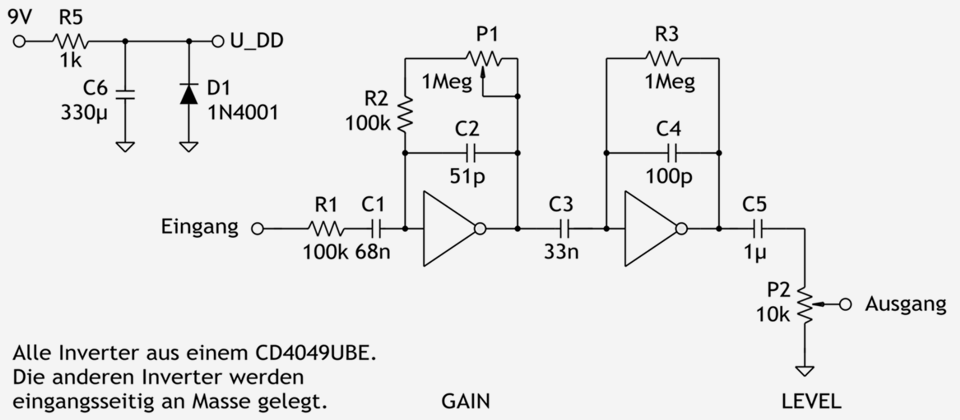
Abb. 2.1: Hier noch einmal Schaltung des Red Llama – in der Version von musikding.de (Entspricht Abbildung 1.2 im ersten Teil.).
High und Low
Um die Schaltung des Red Llama zu verstehen, ist es notwendig, sich ein wenig mit der Theorie der verwendeten Halbleiter zu befassen.
Es handelt sich hier um im Allgemeinen um den Schaltkreis CD4049UBE (der Zusatz UBE – für unbuffered – ist wichtig, für Audio-Anwendungen muss ein ungepufferter Schaltkreis verwendet werden). Der CD4049UBE enthält sechs sogenannte CMOS-Inverter, für das Red Llama werden allerdings nur zwei davon verwendet.
Die Inverter stammen eigentlich aus der Digitaltechnik. Dort gibt es per Definition nur zwei Signalzustände, Low (fast keine Spannung) und High (volle Spannung). Wichtiger ist, dass der Spannungsbereich dazwischen „verboten“, weil undefiniert ist. Die CMOS-Schaltkreise sind dabei so dimensioniert, dass ihre Ausgangspannung möglichst selten in diesem Bereich liegt.
Das gilt auch für die Inverter des CD4049UBE. Sie haben nun die Aufgabe, ein Digitalsignal zu invertieren und dabei den „verbotenen“ Spannungsbereich an seinem Ausgang zu vermeiden. Das heißt, dieser Bereich dazwischen soll – beim Wechsel zwischen Low und High oder High und Low – schnell durchfahren werden. Wenn also die Eingangsspannung von null Volt in Richtung der Betriebsspannung steigt, so soll der Inverter an seinem Ausgang noch lange auf Betriebsspannung verharren, und dann bei einer bestimmten Eingangsspannung „möglichst schnell“ auf eine sehr kleine Ausgangsspannung wechseln. Das heißt, bei einer weiteren Erhöhung der Eingangsspannung soll die Ausgangsspannung des Inverters quasi „herunterfallen“.
Dazu in der folgenden Abbildung 2.2 die gemessene statische Kennlinie eines der sechs Inverters des CD4049UBE (das heißt, die Ausgangsspannung eines Inverters, abhängig von dessen Eingangsspannung). Der Graph „Verstärkung“ und die Hilfslinie für den Arbeitspunkt sollen zunächst ignoriert werden:
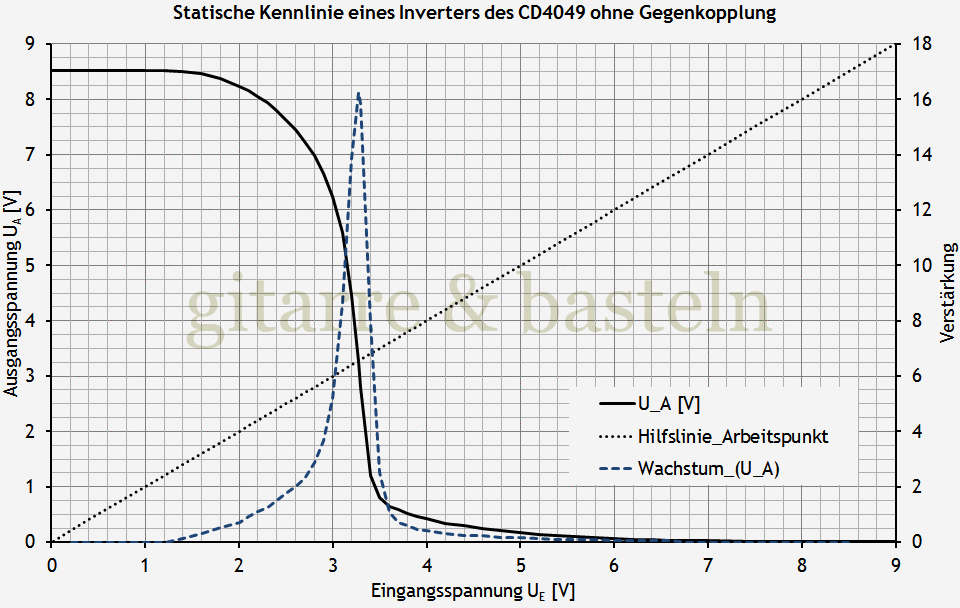
Abb. 2.2: Gemessene statische Kennlinie eines Inverters des Sechsfachinverters 4049 (Ungepufferte Ausführung HCF4049UB von STMicroelectronics). Ein- und Ausgangsspannung in Volt. Betriebsspannung etwa 8,5 Volt.
Wenn also die Eingangsspannung UE, beginnend von null Volt, ansteigt, bleibt die Ausgangspannung UA zunächst unverändert, fällt dann bei einer Eingangsspannung größer 2 Volt erst langsam und später schneller und liegt dann, bei einer Eingangsspannung von 3,5 Volt, weit unter 1 Volt.
Wie kommt dieses Verhalten zustande und wie stabil ist es? Der ungebufferte CMOS-Inverter besteht aus zwei MOSFET-Transistoren (siehe Abbildung 2.3) – ein p-Kanal-MOSFET mit der Source an der Betriebsspannung und ein n-Kanal-MOSFET mit der Source gegen Masse. Die Gates beider MOSFET-Transistoren sind verbunden und bilden den Eingang des Inverters, die verbundenen Drains den Ausgang.
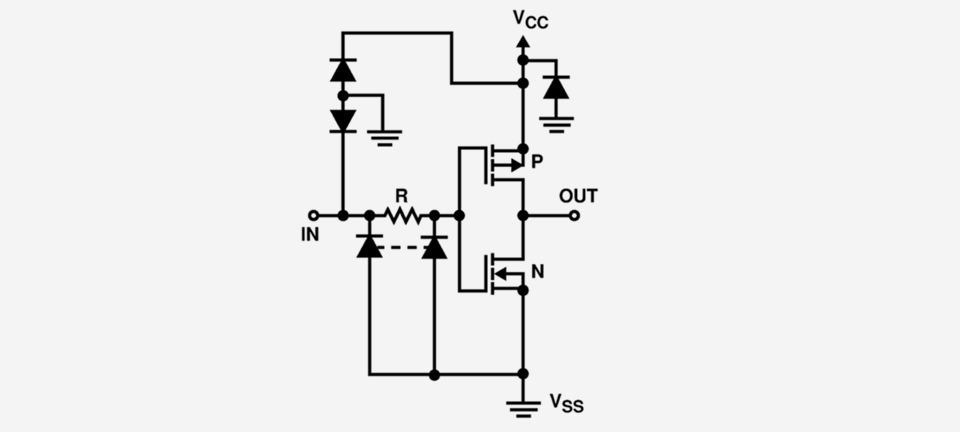
Abb. 2.3 Prinzipielle Innenschaltung eines Inverters des CD4049. Das Prinzipschaltbild wurde dem Datenblatt des Herstellers Texas Instruments entnommen. Die Dioden und der Widerstand R dienen dem Schutz des Inverters vor Überspannungen und Falschpolung.
Bei einer Eingangsspannung um null Volt sperrt der „untere“ n-Kanal-MOSFET und der „obere“ p-Kanal-MOSFET leitet – der Ausgang wird auf High (d. h. etwa auf Betriebsspannung) gezogen. Bei einer Eingangsspannung in Höhe der Betriebsspannung ist es umgekehrt – der obere p-Kanal-MOSFET sperrt, der untere leitet und zieht den Ausgang auf Masse (Low).
Das ist der Standardbetrieb dieser Schaltung als digitaler Inverter. Interessant ist jetzt das Verhalten des Inverters, wenn beide MOSFET-Transistoren leiten, d. h. im „verbotenen“ Bereich. Im verbotenen Bereich fließt ein „Querstrom“ vom Betriebsspannungsanschluss durch beide MOSFET-Transistoren am Ausgang vorbei gegen Masse. Wie groß dieser Strom ist, wird für jeden MOSFET durch die Eingangsspannung (genaugenommen durch die Gate-Source-Spannung) und im geringen Maße durch die Ausgangsspannung (die Drain-Source-Spannung) bestimmt. Dabei sollte insbesondere bei einem MOSFET der Einfluss der Drain-Source-Spannung auf den Drain-Strom infolge des hohen Ausgangswiderstands eher gering sein – soll heißen, der Drain-Strom ist gegenüber Änderungen der Drain-Source-Spannung relativ stabil.
Welches statische Verhalten (Verhältnis von Ausgangsspannung und Eingangsspannung) im „verbotenen“ Bereich ergibt sich daraus? Im verbotenen Bereich zwischen High und Low (beide MOSFET-Transistoren leiten – mit gleichem Drainstrom), führt jede Änderung der Eingangsspannung dazu, dass sich zunächst die Drainströme beider MOSFET-Transistoren gegensinnig ändern müssten, aber nicht können – ist der Ausgang unbeschaltet, kann der Differenzstrom „nirgendwo hin“. Die Änderung des Drainstroms muss dann also mit einer großen Änderung der Drain-Source-Spannung (großen Änderung infolge eines großen Ausgangswiderstandes) kompensiert werden.
Diese notwendige Kompensation führt zum statischen Verhalten des Inverters, insbesondere zum steilen Anstieg im Mittelteil der Kennlinie – siehe Abbildung 2.2. (Diese Kennliniensteilheit ist natürlich von der Größe der Last hinter dem Inverter abhängig, bei einer niederohmigen Last funktioniert das nicht; hier müssen keine unterschiedlichen Drainströme kompensiert werden – die unterschiedlichen Ströme fließen über die Last ab.) Nichtdestotrotz ist eine Verstärkung an diesem „steilen“ Mittelteil der Kennlinie eines solchen Inverters möglich (soviel sei schon einmal vorgegriffen), wenn dafür gesorgt wird, das die Ruhespannungen an Ein- und Ausgang gleich sind und das Eingangssignal zur Eingangsruhespannung addiert wird.
Grundsätzliches über das Verhalten der MOSFET-Transistoren lässt sich nun über die Ausgangskennlinien der beiden MOSFET-Transistoren ableiten – siehe dazu die folgende Abbildung 2.4.

Abb. 2.4: Ausgangskennlinien der beiden MOSFET-Transistoren eines Inverters CD4049 – p-Kanal MOSFET links und n-Kanal MOSFET rechts. Die Diagramme wurden dem Datenblatt des Herstellers Texas Instruments entnommen.
Mit dem unteren n-Kanal-MOSFET soll begonnen werden. Dessen Drainstrom ist, bei einer Gate-Source-Spannung von 5 V, d. h. in der oberen Hälfte des verbotenen Bereiches, auf 20 mA begrenzt. Das bedeutet, dass der untere MOSFET bei Drain-Source-Spannungen größer 3 V einen hohen Innenwiderstand hat (kleine Änderungen des Drainstroms stehen im Zusammenhang mit großen Änderungen der Drainspannung). Kleinere Drainströme hingegen verlangen eine relativ kleine Ausgangsspannung (Drain-Source-Spannung) von maximal 3 V.
Der obere p-Kanal-MOSFET erreicht einen Drainstrom von bspw. 20 mA mit einer Gate-Source-Spannung von 5 V überhaupt nicht, man kann vermuten, dass dazu sowohl eine größere Gate-Source-Spannung wie auch eine größere Drain-Source-Spannung nötig sind. Weiterhin sind die Kennlinien für einen weiteren Bereich der Drain-Source-Spannung gekrümmt und nicht waagerecht; der Innenwiderstand des unteren MOSFET ist, so, wie es im Diagramm dargestellt wird, kleiner.
Eine Betriebsspannung von etwa 9 V vorausgesetzt, werden gleiche Drainströme für beide MOSFET-Transistoren u. a. dann erreicht, wenn Ein- und Ausgangsspannung des Invertes bei etwa 3 V liegen – hier sind die Gate-Source-Spannung und die Drain-Source-Spannung des unteren n-Kanal-MOSFET klein und die des obren p-Kanal-MOSFET groß genug.
Die unterschiedlichen Innenwiderstände beider MOSFET-Transistoren wiederum könnten ein Grund für die unterschiedlich harte und – im unteren Bereich der Kennlinie – zum Teil diskontinuierliche Begrenzung sein.
CMOS als Verzerrer
Was bedeutet das nun für die Gitarrenbastler? Es bedeutet erst einmal, dass der Inverter für den kleinen Eingangsspannungsbereich von 3 Volt bis 3,5 Volt eine sehr hohe (negative) Verstärkung hat, die dann an den Rändern dieses Bereiches mehr oder weniger sanft abnimmt. Das klingt für Freaks, die aus allem Verzerrer bauen wollen (natürlich immer irgendwie „röhrenähnlich“), interessant.
Wie aber bekommt man den Arbeitspunkt automatisch in diesen hochverstärkenden Bereich genau dieses Schaltkreises? (Das Gitarrensignal ist ja eigentlich ein Wechselspannungssignal, ihm muss also genau diese Spannung von 3 Volt bis 3,5 Volt vor dem Eingang des Inverters aufaddiert werden.)
Der Arbeitspunkt
Wenn man dafür sorgt, dass CMOS-Eingang und CMOS-Ausgang im Ruhezustand die gleiche Spannung haben und diese nicht durch eine Eingangs(gleich)spannung beeinflusst werden kann, dann könnte der CMOS-Inverter als Verstärker- bzw. Verzerrerstufe funktionieren.
Dazu sei noch einmal auf Abbildung 2.2 verwiesen – die statische Kennlinie des Inverters. Hier gibt es die schon erwähnte „Hilfslinie Arbeitspunkt“; sie stellt die Funktion Eingangsspannung gleich Ausgangsspannung dar. Das heißt, wird der Eingang des Inverters mit dem Ausgang verbunden, so treffen sich Kennlinie und Hilfslinie bei der Ein- bzw. Ausgangsruhespannung, dem Arbeitspunkt. Bei dem konkreten (ausgemessenen) CMOS-Inverter treffen sich beide bei etwa 3,3 Volt. Das ist Arbeitspunkt dieses Inverters. Mitten im „verbotenen“ Spannungsbereich.
Es ist also ganz einfach, man nimmt einen solchen Inverter, verbindet Eingang und Ausgang über einen (hohen) Widerstand und legt damit CMOS-Eingang und CMOS-Ausgang „gleichstrommäßig“ auf die gleiche Spannung. Vor den CMOS-Eingang kommt nach ein Koppelkondensator und fertig ist die zweite Stufe des Red Llama, also quasi das Hinterteil.
Das Diagramm in Abbildung 2.2 enthält noch einen dritten Graphen, der mit „Verstärkung“ bezeichnet wurde – er beschreibt die Änderung der Ausgangsspannung über der Eingangsspannung, also die Verstärkung in Abhängigkeit von der Eingangsspannung. Man kann erkennen, dass die Verstärkung in einem sehr kleinen Eingangsspannungsbereich sehr groß ist, in einer Richtung (größere Eingangsspannung) sehr schnell und nach der anderen langsamer abnimmt. Man muss wohl mit einem frühen Einsatz der Verzerrungen, einer eher kratzigen Verzerrung (auch kratzigem „Anzerren“) und u. U. auch mit höherem Rauschen rechnen.
Wichtig für eine „musikalische“ Verstärkung und Verzerrung scheint nun zu sein, dass die Verstärkung im Arbeitspunkt am größten ist, oder, anders gesagt, dass im Arbeitspunkt, wo Eingangs- und Ausgangsruhespannung gleich sind, auch die Verstärkung auch am größten ist. Das bedeutet, dass das Signal umso stärker begrenzt werden soll, je größer es ist.
Um das Oszillografen-bildlich zu beschreiben: ein Sinussignal am Eingang eines Verzerrers soll, beginnend in den Signalspitzen, begrenzt und nicht an den Spitzen „nach oben oder unten gezerrt“ werden; letzteres scheint nicht besonders gut zu klingen. Letzteres würde aber passieren, wenn der Arbeitspunkt weit genug neben dem Punkt mit der größten Kennliniensteilheit / Verstärkung liegt. Bei den wenigen getesteten Exemplaren des HCF4049UB von STMicroelectronics schien das immer zu passen, allerdings weist der Hersteller im Datenblatt ausdrücklich darauf hin, dass der genaue Verlauf der Kennlinie nicht garantiert werden kann. Der Schaltkreis ist ja ursprünglich auch nicht für Audioanwendungen vorgesehen.
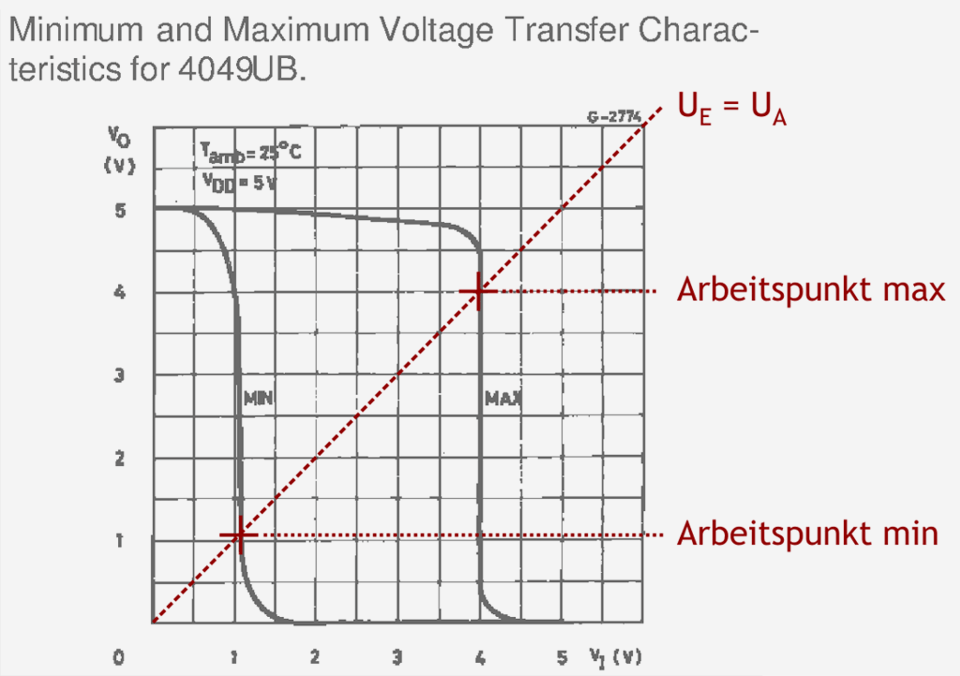
Abb. 2.5: Vom Hersteller SGS-Thomson im Datenblatt vorgegebene Toleranzen der statischen Kennlinie eines 4049UB bei UDD = 5 Volt und die sich daraus ergebenen Arbeitspunkte. In der Zeichnung sind die Arbeitspunkte als Schnittpunkte mit einer Hilfsdiagonalen UA = UE eintragen.
In obiger Abbildung 2.5 sind, am Beispiel eines Auszugs aus dem Datenblatt HCF4049UB des Herstellers SGS-Thomson, die maximalen und minimalen statischen Kennlinien bei einer Betriebsspannung von 5 Volt dargestellt; man erkennt, dass alles, was der Hersteller garantiert, die Einhaltung der Pegel für Low und High am Ausgang (kleiner als 1 Volt bzw. größer als 4 Volt bei einer Betriebsspannung von 5 Volt), wenn die Eingangsspannung ebenfalls in den für Low und High gesetzten Grenzen bewegt. Das heißt, auf eine Eingangsspannung kleiner 1 Volt folgt eine Ausgangsspannung größer 4 Volt und umgekehrt. Für das klangliche Verhalten in einem Gitarrenverzerrer macht der Hersteller also keine Angaben.
Für eine Anwendung als Audioverstärker oder als Verzerrer muss also immer mit dem konkreten Bauelement getestet werden. Das könnte neben dem Rauschproblemen von CMOS-Schaltungen einer der Gründe sein, warum die CMOS-Inverter in der kommerziellen Gitarrenelektronik bisher eher eine Exotenrolle spielen – eine Serienproduktion mit individuell anzupassenden Bauelementen ist aufwendig, sogar auch dann, wenn aus ambitionierten „erfolgreichen Freaks“ Gerätehersteller werden.
Ein ähnlicher Datenblattausschnitt für einen ähnlichen Schaltkreis (HCF4007UB, ein MOSFET-Array, das zu drei CMOS-Invertern verschaltet werden kann) in der folgenden Abbildung 2.6 lässt vermuten, dass sich das Problem der Toleranzen auch bei höherer Betriebsspannung fortbesteht – die maximalen und minimalen Arbeitspunkte liegen hier bei größeren Betriebsspannungen sogar deutlich außerhalb des hochverstärkenden Bereichs. (Den hochverstärkenden Bereich markieren die nahezu senkrechten Abschnitte der Kennlinie).
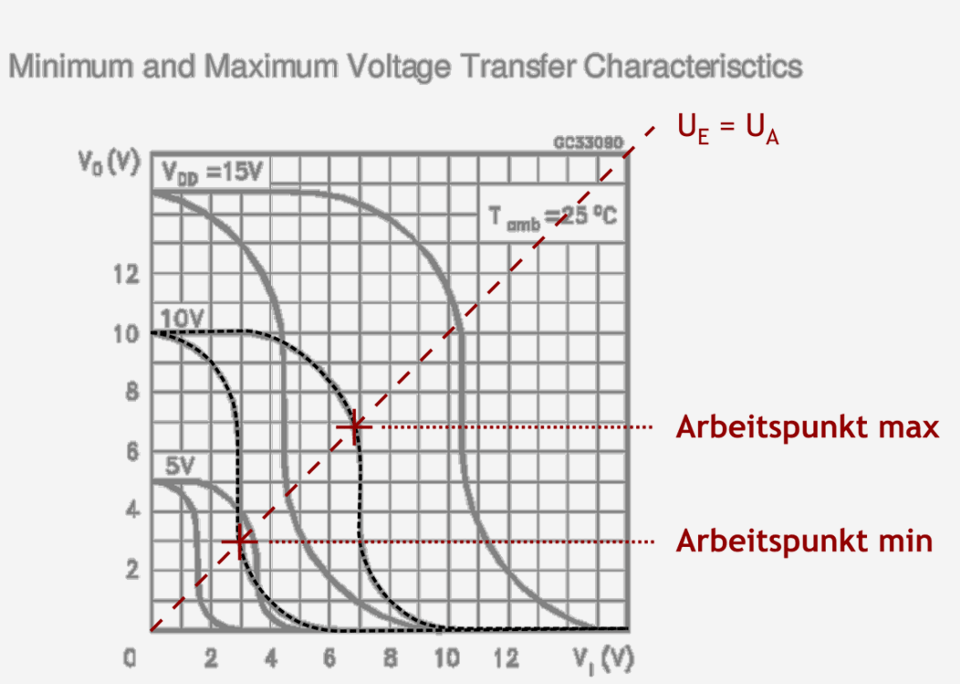
Abb. 2.6: Vom Hersteller SGS-Thomson im Datenblatt vorgegebene Toleranzen der statischen Kennlinie eines HCF4007UB bei verschiedenen Betriebsspannungen. In der Zeichnung sind die Kennlinien für die Betriebsspannung von 10 Volt hervorgehoben und die Arbeitspunkte als Schnittpunkte mit einer Hilfsdiagonalen UA = UE eintragen.
Gegenkopplung und Verstärkung
Zumindest die erste Stufe des Red Llama, quasi dessen Vorderteil, um mal bei obigem Bild zu bleiben, müssen aber doch Zügel angelegt werden, soll heißen, die erste Stufe des CMOS-Verzerrers wird in ihrer „wilden“ Verstärkung / Verzerrung kontrolliert werden und hat einen Gain-Regler bekommen.
Dazu verwendet man üblicherweise eine Gegenkopplung: Bei Verstärkern mit einem Differenzeingang führt man dazu einen Teil der Ausgangsspannung auf den „negativen“ Eingang zurück. Damit wird Verstärkung des Gesamtsystems etwas kleiner als das Reziproke der Gegenkopplung, will sagen, wenn beispielsweise ein Zehntel des Ausgangssignals auf den negativen Eingang zurückgeführt wird, kann die resultierende Verstärkung nur kleiner als zehn sein.
Eine solche Gegenkopplung verringert aber nicht nur die Verstärkung, nichtlineare System wie ein CMOS-Inverter werden dadurch auch stabilisiert – die Verzerrungen wandern „nach außen“ an den Rand des Aussteuerungsbereiches.
Für die Gegenkopplung eines CMOS-Inverters wird eine Schaltung verwendet, die der invertierenden Schaltung eines Operationsverstärkers ähnlich sieht; es gibt einen Widerstand zwischen Schaltungseingang und Invertereingang und einen zwischen Invertereingang und Ausgang. Die maximale Verstärkung ist hier aber kleiner als das Verhältnis dieser beiden Widerstände, da der CMOS-Inverter im Gegensatz zum Operationsverstärker keine unendlich große Leerlaufverstärkung hat. (Genaugenommen addieren sich hier das Maß der Gegenkopplung und die Reziproke der Verstärkung ohne Gegenkopplung zur Reziproken der resultierenden Gesamtverstärkung. Erreicht also der Inverter eine maximale Verstärkung von fünfzehn, so wird bei einer Gegenkopplung von eins zu elf die maximale Verstärkung gleich 1/(1/11 + 1/15), also etwas mehr als sechs sein.)
Zurück zur Schaltung des Red Llama. Das Eingangssignal läuft über einen Kondensator 68 nF und einen Widerstand 100 kΩ an den Eingang des ersten Inverters, zwischen Eingang und Ausgang des ersten Inverters liegen ein Widerstand 100 kΩ und ein Potentiometer 1 Megaohm, so dass für die erste Stufe eine Gegenkopplung von elf zu eins bis maximal eins zu eins eingestellt werden kann.
Der Kondensator im Eingang hat zuerst einmal die Aufgabe, die Gleichspannung vom Eingang fernzuhalten und Beeinflussungen des Arbeitspunktes über den Eingang zu verhindern.
Mit den beiden Widerständen Rvor (vor dem Eingang des Inverters) und RE-A (zwischen dessen Ein- und Ausgang) wird die Gegenkopplung des Inverters realisiert. Wie sich die Kennlinie eines solchen Inverters durch Gegenkopplung ändert, zeigt die folgende Abbildung 2.7. Hier wurde aus den Messwerten der Kennlinie ohne Gegenkopplung eine Kennlinie für eine Gegenkopplung von eins zu zehn abgeleitet, indem aus den Ein- und Ausgangsspannungen des eigentlichen Inverters jeweils eine neue Eingangsspannung für den gegengekoppelten Inverter (d. h. vor dem Vorwiderstand) berechnet wurde:
\( \begin{equation} u_{\textrm{e}} = u_{\textrm{E,CMOS}} + \left( u_{\textrm{E,CMOS}} - u_{\textrm{A,CMOS}} \right) \cdot{} \cfrac{R_{\textrm{vor}}} {R_{\textrm{E-A}}} \tag{1}\end{equation} \)
Man sieht in der Darstellung der berechneten Kennlinie, dass die maximale Verstärkung des gegengekoppelten Inverters kleiner geworden ist, sich aber besser in das Gesamtverhalten einpasst; die Kennlinie ist ein wenig homogener geworden.
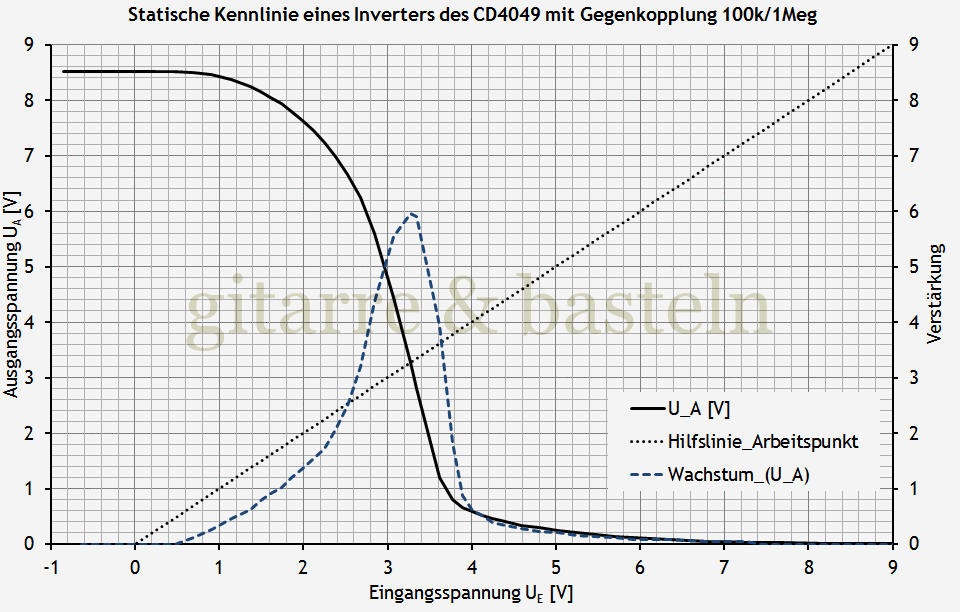
Abb. 2.7: Gemessene und berechnete statische Kennlinie eines Inverters HCF4049UB mit Spannungsgegenkopplung 100 kΩ zu 1 MΩ. Ein- und Ausgangsspannung in Volt. Betriebsspannung etwa 8,5 Volt.
Erst bei einer wesentlich stärkeren Gegenkopplung wird die statische Kennlinie wirklich „gerader“, wie die folgende Abbildung 2.8 zeigt. Hier resultiert aus einer Gegenkopplung von eins zu drei eine maximale Verstärkung der Stufe von 2,5; solche stark gegengekoppelten Stufen werden bei Schaltungen mit dem CD4049UBE gern als abschließende Begrenzerstufen eingesetzt, die den vorher eher ruppig verzerrten Klang ein wenig komprimieren.
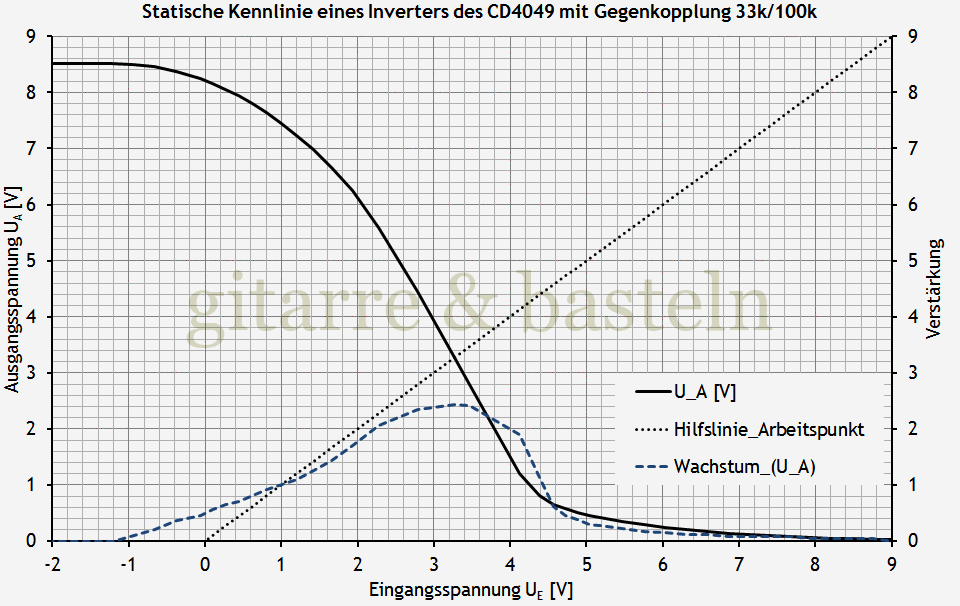
Abb. 2.8: Gemessene und berechnete statische Kennlinie eines Inverters HCF4049UB mit Spannungsgegenkopplung 33 kΩ zu 100 kΩ. Ein- und Ausgangsspannung in Volt. Betriebsspannung etwa 8,5 Volt.
Saging und Sägen durch Betriebsspannung und Kennlinie
Ein wesentlicher Unterschied zwischen verschiedenen Anwendungen verschiedener CMOS-Inverter (z. B. zwischen dem originalen Red Lama und einer einfachen Version von Craig Anderton's Tube Sound Fuzz) ist der Vorwiderstand in der Betriebsspannungszuleitung.
Die CMOS-Inverter werden ja, anders als in ihrer „digitalen“ Anwendung, in der Gitarrenelektronik in einer Art „verbotenen Bereich“ von Ein- und Ausgangsspannung betrieben. Verboten nicht nur im Sinne eines undefinierten Signalzustandes zwischen High und Low, sondern auch im Hinblick auf die Stromaufnahme.
Dazu ein wenig mehr über die Funktion des CMOS-Inverters: Die ungepufferten Inverter bestehen aus zwei MOSFETs, die zwischen Betriebsspannung und Masse in Reihe geschaltet sind – zwischen Betriebsspannung und Ausgang liegt ein p-Kanal-MOSFET (Source an Betriebsspannung, Drain am Ausgang) und zwischen Ausgang und Masse ein n-Kanal-MOSFET (Drain an Ausgang, Source an Masse). Beide bilden einen Spannungsteiler zwischen Betriebsspannung und Masse, dessen Ausgang den Ausgang des Inverters darstellt.
Die Gates beider MOSFETs sind verbunden mit dem Invertereingang. Je nach logischem Zustand am Eingang (Hi oder Lo) steuert entweder der obere oder der untere MOSFET durch, während der jeweils andere MOSFET sperrt. Der Ausgang ist so entweder mit Masse oder Betriebsspannung verbunden. Da eben auch immer nur einer der beiden MOSFETs leitet und der andere sperrt, fließt zwischen Betriebsspannung und Masse kein Strom.
In dem hier benutzten undefinierten Zustand (Inverter als Verstärker / als Verzerrer) leiten die MOSFETs mehr oder weniger stark, was zu einer deutlichen Stromaufnahme des Inverters führt – es fließt ein Querstrom durch beide MOSFETs von Betriebsspannung nach Masse. Dieser Strom steigt dabei natürlich mit der Betriebsspannung. Mit einem großen Widerstand zwischen Betriebsspannung und Inverterschaltkreis können so Stromaufnahme und Arbeitsspannung verringert werden.
So lag bei einem Red Llama (Bausatz des Versenders musikding.de) zwischen der Betriebsspannung und dem CD4049UBE ein Widerstand von 1 kΩ – der Schaltkreis lief hier mit einer Betriebsspannung von lediglich 6 Volt – mit einer Stromaufnahme von 3 mA. Nachdem dieser Widerstand auf 100 Ω verringert worden war, wurde am Schaltkreis eine Betriebsspannung von etwa 8,5 Volt gemessen – die beiden Inverter verbrauchen so zusammen 5 mA.
Das hat Folgen auf den Aussteuerungsbereich bzw. Headroom der Inverter und auch auf deren statische Kennlinie und damit auf Härte und Symmetrie der Verzerrungen, wie die folgende Abbildung 2.9 (graphische Darstellung gemessener Kennlinien) zeigt:
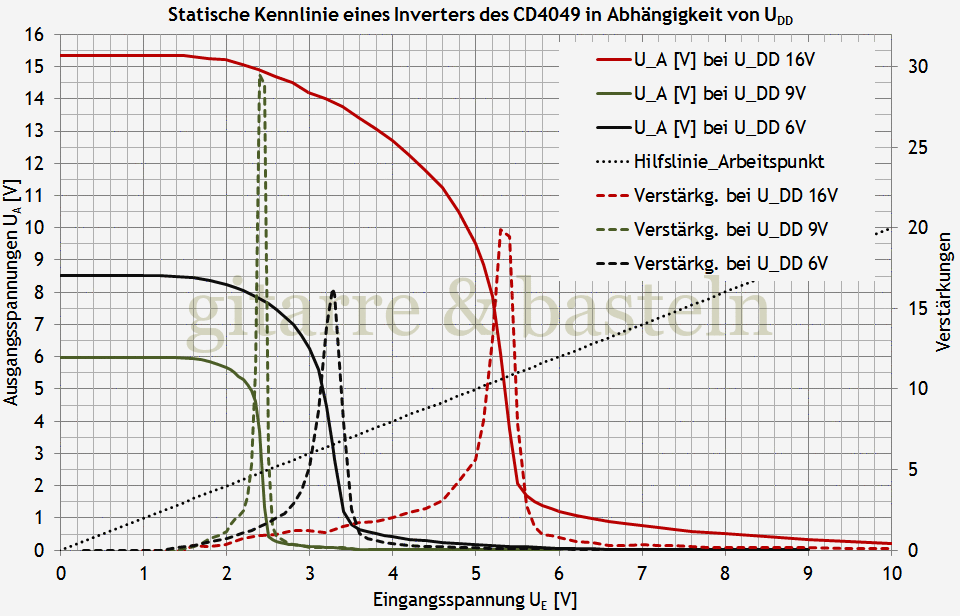
Abb. 2.9: Gemessene statische Kennlinie eines Inverters HCF4049UB bei verschiedenen Betriebsspannungen. Ein- und Ausgangsspannung in Volt.
Die Gründe für dieses Verhalten sollen hier nicht diskutiert werden, sie sind auch bei anderen ungepufferten CMOS-Invertern zu beobachten. Es sei lediglich angemerkt, dass man bei der MKII-Version des Red Llamas (soweit man das nach den Gutshots auf www.freestompboxes.org beurteilen kann), auf einen solchen Vorwiderstand zwischen Betriebsspannung und Inverterschaltkreis gänzlich verzichtet hat.
Allerdings entsteht der Eindruck, dass dem Leiterplatten-Layouter hier ein Fehler unterlaufen ist – ein Widerstand R6 = 100 Ω liegt nicht zwischen Batterie / Netzteil und dem Betriebsspannungseingang Pin 1 des CMOS-Schaltkreises (Pin 1 ist bei diesem Gerät direkt mit der Betriebsspannung verbunden), sondern er verbindet die Betriebsspannung mit den Eingängen der nicht verwendeten Inverter (diese nicht verwendeten Inverter sollten immer entweder mit Masse oder der Betriebsspannung verbunden, damit die Inverter einen definierten Zustand haben und stromlos sind). Dabei hat ein Widerstand 100 Ω vor den Invertereingängen wenig Sinn, weil diese ohnehin keinen Strom aufnehmen.
Der Eingangswiderstand
Nach den Betrachtungen zu Kennlinie, Verstärkung und Einfluss der Betriebsspannung, die sich einfach an der Schaltung des Red Llama darstellen ließen, nun zu Überlegungen zu Eingangswiderstand und Frequenzgang – zunächst anhand der Schaltung des Red Llama.
Betrachtet man die erste Stufe des Red Llama (siehe obige Abbildung 2), so liegt es nahe, dass diese Stufe, in Analogie zur invertierenden Schaltung des Operationsverstärkers, einen Widerstand von 100 kΩ hat.
Insgesamt gesehen gibt es aber Unterschiede zwischen der beschriebenen Schaltung mit einem CMOS-Inverter und der invertierenden Schaltung des Operationsverstärkers, die zu einem größeren Eingangswiderstand führen, wie im Folgenden begründet werden soll.
Zuerst ist die Leerlaufverstärkung des CMOS-Inverters gegenüber der des Operationsverstärkers wesentlich kleiner und eigentlich auch nirgendwo linear. Dazu kommt, dass der Operationsverstärker zwei Differenzeingänge besitzt (einen invertierenden und einen nichtinvertierenden), wobei in der invertierenden Schaltung des Operationsverstärkers dessen nichtinvertierender Eingang auf ein Ruhepotential gelegt wird. Der Operationsverstärker „versucht“ dann mit seiner hohen Differenzverstärkung, den Ausgang so „nachzuregeln“, dass auch am invertierenden Eingänge Ruhepotential anliegt. Der Eingangsstrom fließt also durch den ersten Widerstand der invertierenden Schaltung in ein Nullpotential und dann durch den zweiten Widerstand zum Ausgang der Schaltung. Daraus folgt, dass der Wert des Eingangswiderstandes der invertierenden Schaltung gleich dem Wert des Widerstands zwischen Schaltungseingang und invertierendem Eingang des OPV ist.
Der CMOS-Inverter hat aber keinen nichtinvertierenden Eingang, auch ist seine die Leerlaufverstärkung wesentlich kleiner, so dass ein Punkt mit der (Signal)spannung null (im Folgenden Signal-null-Punkt) nicht dem (invertierenden) Eingang des Inverters entspricht, sondern „hinter“ dem Eingang des Inverters liegt, ein Stück in Richtung Inverterausgang. Wenn der CMOS-Inverter also eine negative Leerlaufverstärkung von v0 hat, so teilt sich die Spannung zwischen Eingang und Ausgang des Inverters so auf, dass sich die Spannung zwischen Invertereingang und Signal-null-Punkt und die Spannung zwischen Signal-null-Punkt und Inverterausgang zueinander verhalten wie eins zu |v0|.
Für den Eingangskreis der gegengekoppelten Inverterschaltung folgt daraus: Die Eingangsspannung der gegengekoppelten Inverterschaltung setzt sich zusammen aus der Spannung zwischen Schaltungseingang und Invertereingang (der Spannung über R1) und der Spannung zwischen Invertereingang und Signal-null-Punkt, welche wiederum die durch |v0| + 1 geteilte Spannung zwischen Inverterein- und -ausgang (d. h. über R2 und P1) ist:
\( \begin{equation} u_{\textrm{e}} = u_{\textrm{R1}} + \cfrac{u_{\textrm{R2}}+u_{\textrm{R10}}} {1-v_0} \tag{2}\end{equation} \)
Die Gleichung wird durch uR1 dividiert:
\( \begin{equation} \cfrac{u_{\textrm{e}}} {u_{\textrm{R1}}} = 1 + \cfrac{u_{\textrm{R2}}+u_{\textrm{R10}}} {u_{\textrm{R1}}} \cdot \cfrac{1} {1-v_0} \tag{3}\end{equation} \)
Anschließend wird das Verhältnis der Spannungen über den Widerständen, durch die der gleiche Strom fließt, durch das Verhältnis der Widerstände ersetzt:
\( \begin{equation} \cfrac{u_{\textrm{e}}} {u_{\textrm{R1}}} = 1 + \cfrac{R_2 + R_{\textrm{10}}} {R_1} \cdot \cfrac{1} {1-v_0} \tag{4}\end{equation} \)
Dieser Zusammenhang zwischen Widerständen und Spannungen gilt auch für den Eingangswiderstand, da der Eingangsstrom (abgesehen von einem Pulldown-Widerstand) vollständig durch R1 fließt:
\( \begin{eqnarray} \frac{r_{\textrm{in}}} {R_1} & = & \frac{u_{\textrm{e}}} {u_{\textrm{R1}}} \\~\\ r_{\textrm{in}} & = & R_1 \cdot \frac{u_{\textrm{e}}} {u_{\textrm{R1}}} \tag{5}\end{eqnarray} \)
Fasst man beide Gleichungen zusammen, ergibt sich für den Eingangswiderstand:
\( \begin{eqnarray} r_{\textrm{in}} & = & R_1 \cdot \left( 1 + \frac{R_2 + R_{\textrm{10}}} {R_1} \cdot \frac{1} {1-v_0} \right) \\~\\ & = & R_1 + \frac{R_2 + R_{\textrm{10}}} {1-v_0} \tag{6}\end{eqnarray} \)
Zusammenfassend kann also gesagt werden, dass der Eingangswiderstand des Red Llama bei gering eingestelltem Gain (P1) sowie bei kleinen Signalspannungen / im Arbeitspunkt am geringsten ist, aber immer größer als 100 kΩ (der Widerstand R1 des Red Llama).
Auf die Schaltung des Verzerrers bezogen, so zeigt sich natürlich auch hier, dass der Eingangswiderstand dieser Eingangsstufe größer als der Widerstand 27 kΩ ist und sich erst durch das vorgeschaltete Potentiometer 100kΩ relativ stabil im Bereich zwischen 50 kΩ und 100 kΩ bewegt. Damit ist der Eingangswiderstand dieser Schaltung wesentlich größer als beispielsweise der eines Range Master Treble Booster, was bei der Wahl des Eingangskondensators berücksichtigt werden muss (der Eingangskondensator muss entsprechend kleiner sein). Mit einem Eingangskondensator von 6,8 nF wie im Range Master würde hier nur ein Low Cut von höchstens 500 Hz realisiert werden.
Der Frequenzgang
Mit dem ermittelten minimalen Eingangswiderstand kann man nun den Frequenzgang der Eingangsstufe mit direkt angeschlossener Gitarre etwas treffsicherer simulieren – Verwendung findet dazu ein Ersatzschaltbild für einen Humbucker, das seinerzeit aus einigen Einzelspulmodellen aus Manfred Zollners entstehendem Buch „Elektrogitarren“ zusammengefriemelt wurde.
Weiterhin muss das die Eigenkapazität des Gitarrenkabels in die Simulation einbezogen werden, es werden 600 pF angenommen (das entspricht einem guten, kapazitätsarmen 6-Meter-Kabel. Um den Eingangswiderstand der ersten Inverterstufe zu simulieren, wurde anstelle des CMOS-Inverters ein Multiplikator mit einer Verstärkung von —15 verwendet – für diese Simulation wurde davon ausgegangen, dass dieser erste Inverter wegen der eher schwachen Gitarrensignale weitgehend im linearen Bereich arbeitet. Schließlich wurde für die Simulation der Modus mit der stärksten Bassabschwächung angenommen (Treble Booster 2, Eingangskondensator C2 mit 2,2 nF), das klang auf dem Steckbrett mit Humbuckern am besten.
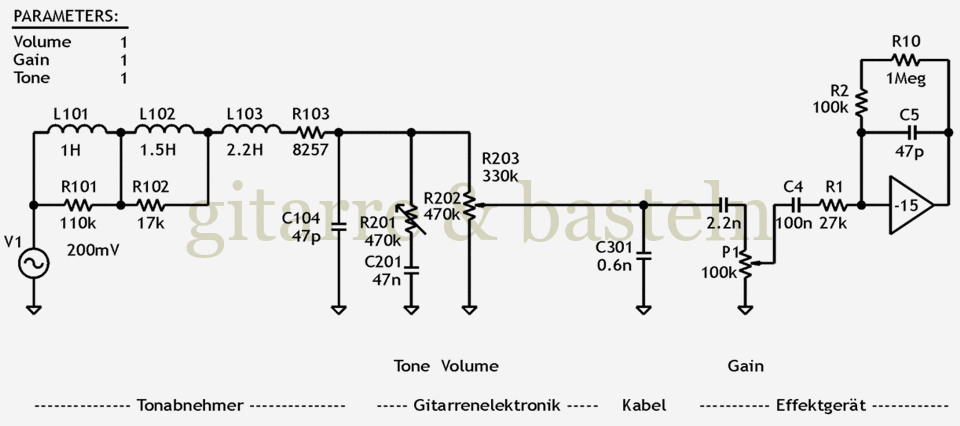
Abb. 2.10: Schaltung zur Simulation des Frequenzgangs von Gitarre und Verzerrereingangsschaltung.
Zunächst der Frequenzgang für verschiedene Einstellungen des Gain-Reglers, Volumen- und Tonregler der Gitarre sind in dieser Simulation immer auf 1 gestellt, d. h. voll aufgedreht:
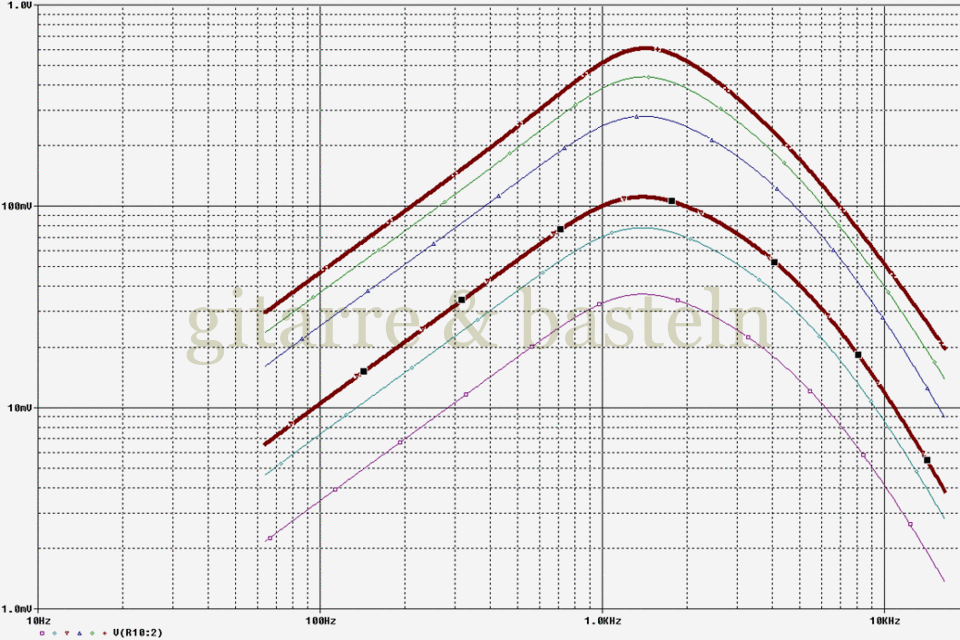
Abb. 2.11: Simulierter Frequenzgang von Tonabnehmer, Gitarrenelektronik (Volumen- und Tonregler auf 1), Kabel sowie Verzerrereingangsschaltung für verschiedene Einstellungen des Gain-Reglers (0,05 0,11 0,16 0,44 0,72 und 1; die Kurven für Maximal- und Mittelstellung sind hervorgehoben; Simulationschaltung siehe Abbildung 2.10).
Zu erkennen ist eine stark mittenorientierte Vorfilterung, die sich auf eine Frequenz von hier etwa 1,5 kHz konzentriert, wobei die Flankensteilheit unterhalb der Mittelfrequenz bei 20 dB pro Dekade liegt (das heißt, das Hochpassverhalten entsteht durch ein [RC-]Filter erster Ordnung), während der Tiefpass oberhalb der Mittelfrequenz steiler ist (ein Filter zweiter Ordnung mit Beteiligung der Tonabnehmerinduktivität).
In den folgenden Diagrammen nun der (simulierte) Einfluss des Volumenreglers der Gitarre, zunächst für maximales Gain. Es ist zu erkennen, dass, neben der Lautstärkereduzierung, die mittenorientierte Vorfilterung an Schärfe verliert, wenn das Volumenpoti zurückgedreht wird. Weiterhin verschiebt sich die Mittenbetonung leicht nach oben, das Signal wird umso heller, je weiter das Volumenpoti zurückgedreht wird.
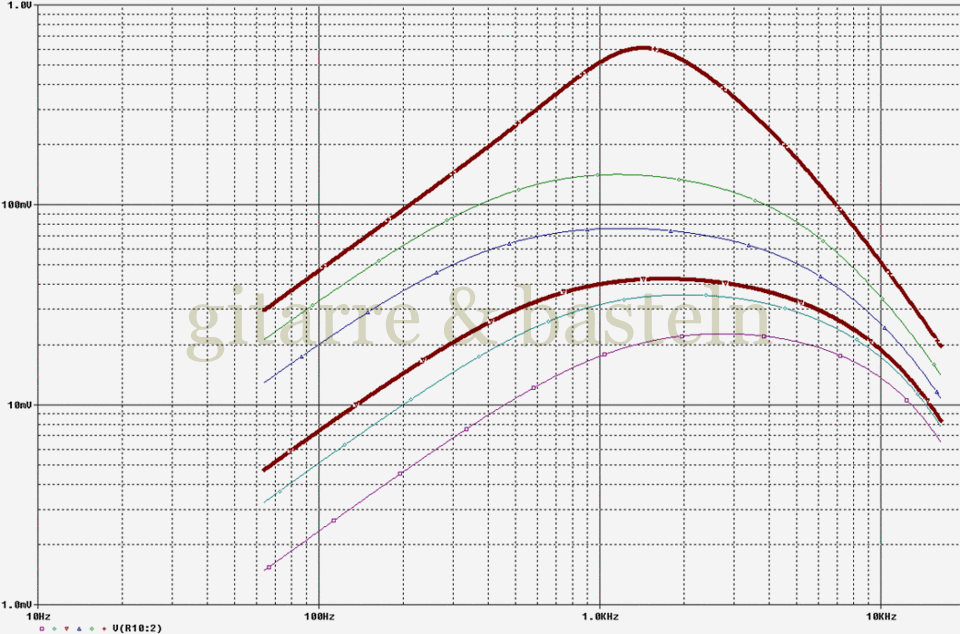
Abb. 2.12: Simulierter Frequenzgang von Tonabnehmer, Gitarrenelektronik (Tonregler auf 1), Kabel sowie Verzerrereingangsschaltung (Gain-Regler auf 1) für verschiedenen Einstellungen des Gitarrenvolumenreglers (0,05 0,11 0,16 0,44 0,72 und 1; die Kurven für Maximal- und Mittelstellung sind hervorgehoben; Simulationschaltung siehe Abbildung 2.10).
Die beiden folgenden Diagramme für Gain-Einstellungen von 0,5 und 0,1 zeigen ein ähnliches Verhalten, nur dass die Schärfe der Mittenanhebung (bei voll aufgedrehtem Volumenpoti) mit zurückgedrehtem Gain-Regler abnimmt. Aber das war ja auch schon in Abbildung 2.11 zu erkennen.
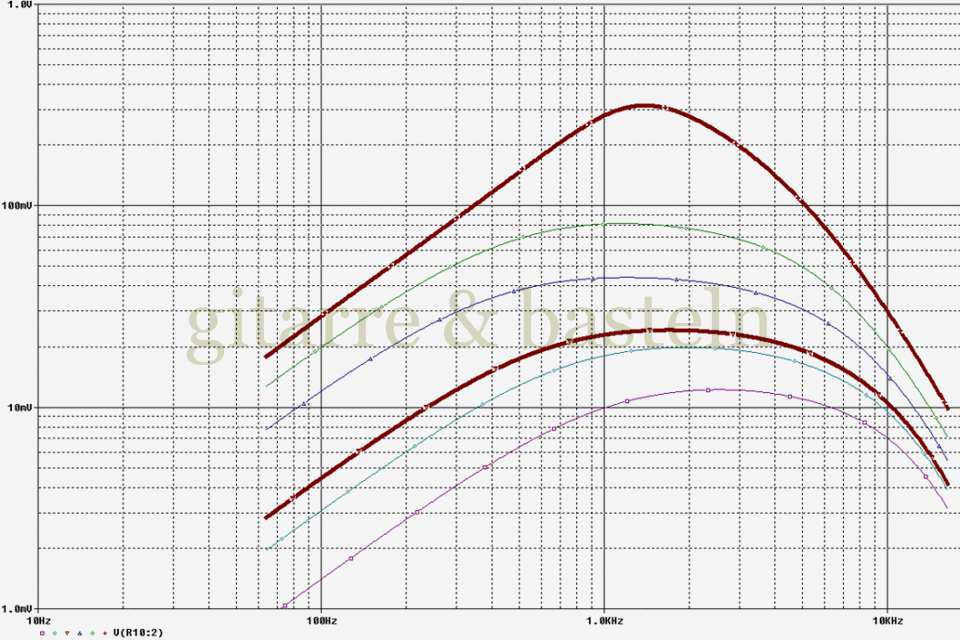
Abb. 2.13: Simulierter Frequenzgang von Gitarre und Verzerrereingangsschaltung bei verschiedenen Stellungen des Gitarrenvolumenreglers (Gain-Regler auf 0.5); ansonsten wie obige Abbildung 2.12.
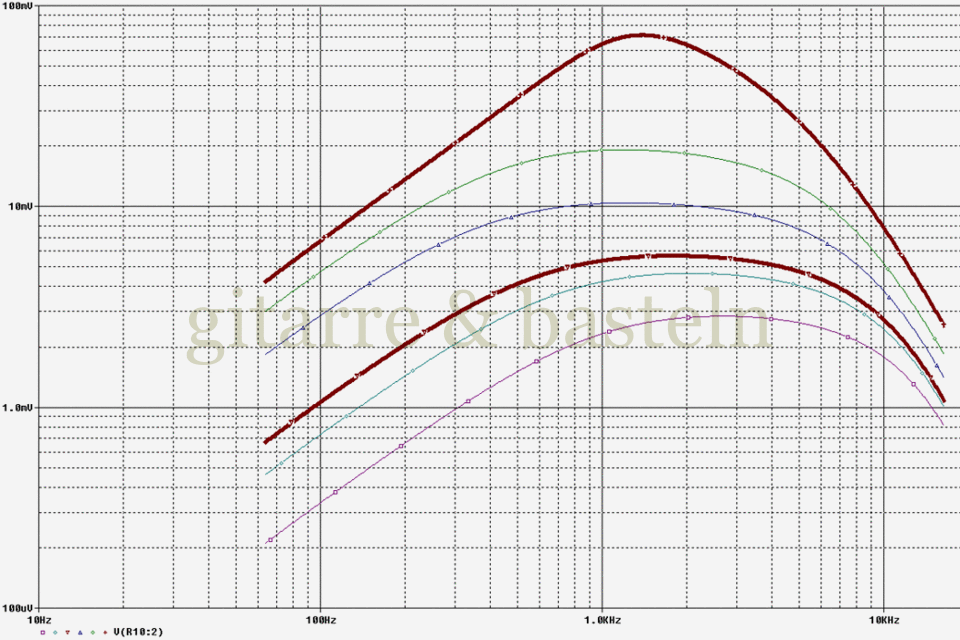
Abb. 2.14: Simulierter Frequenzgang von Gitarre und Verzerrereingangsschaltung bei verschiedenen Stellungen des Gitarrenvolumenreglers (Gain-Regler auf 0.1). Der Maßstab der y-Achse hat sich bei diesem Diagramm um den Faktor 10 geändert (0,1 mV bis 100 mV statt 1 mV bis 1 V); ansonsten wie obige Abbildung 2.12.
Abschließend noch die Frequenzgangssimulation bei verschiedenen Eingangskondensatoren. Hier wird nachvollziehbar, wie die starke Mittenbetonung entsteht – zu dem im Absatz „Treble Booster“ diskutierten Hochpassverhalten kommt noch ein „überlappender“ Tiefpass (Tonabnehmerinduktivität, Kabelkapazität und der geringe Eingangswiderstand des Verzerrers), so dass insgesamt die schon beobachtete Mittenfilterung entsteht, deren Maximum sich mit Vergrößerung des Eingangskondensators zu tieferen Frequenzen hin verschiebt und dabei sowohl größer als auch weniger scharf wird. Das liegt daran, dass sich der durch den Eingangskondensator bedingte Hochpass umso mehr zu tieferen Frequenzen verschiebt, je größer dieser Kondensator ist.

Abb. 2.15: Simulierter Frequenzgang von Gitarre und Verzerrereingangsschaltung für verschiedene Vorschaltkondensatoren (2,2 nF, 4,4 nF und 10,4 nF – Gitarrenvolumen-, Gitarrenton- und Gain-Regler jeweils 1)
Ergänzend und zum Vergleich noch einmal die Frequenzgangssimulation eines Red Llama MK I, angesteuert vom gleichen Humbucker. Für den Eingangsinverter des Red Llama wurde wegen dessen verringerter Betriebsspannung von etwa 6 Volt eine etwas größere Maximalverstärkung von −25 angenommen. (siehe dazu auch die Darstellung weiter oben)
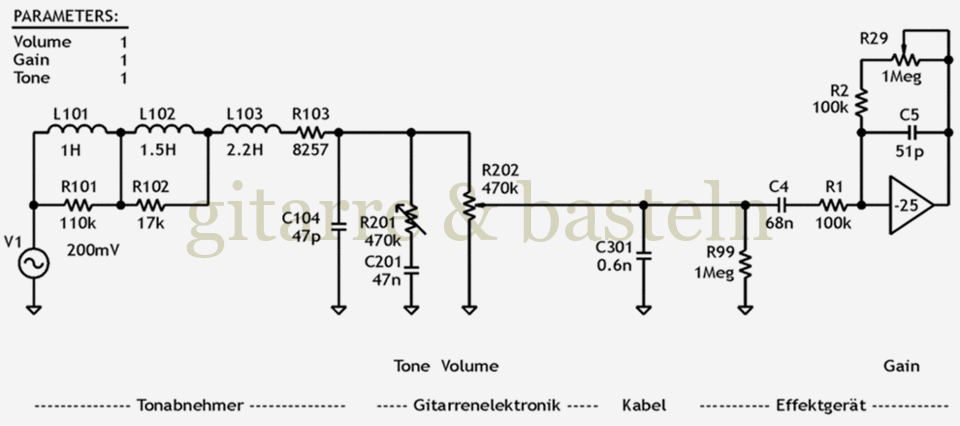
Abb. 2.16: Simulation des Frequenzgangs einer mit Humbuckern bestückten Gitarre am Eingang eines Red Llama.
Im folgenden Frequenzgangdiagramm ist zu erkennen, dass die Eingangsstufe etwas mehr Gain hat, da die Maximalverstärkung des Eingangsinverters größer ist. Außerdem ist der Frequenzgang bis etwa 2 kHz weitgehend linear, da zum einen auf einen (die Bässe beschneidenden) sehr kleinen Eingangskondensator verzichtet wurde und zum anderen der Eingangswiderstand durch die simplere Beschaltung (kein Poti vor dem Eingangsinverter) größer ist und so die Höhenwiedergabe des Tonabnehmers weniger stark bedämpft wird. Lediglich die Resonanz des Tonabnehmers ist „wegbedämpft“, so groß ist der Eingangswiderstand dann doch nicht.
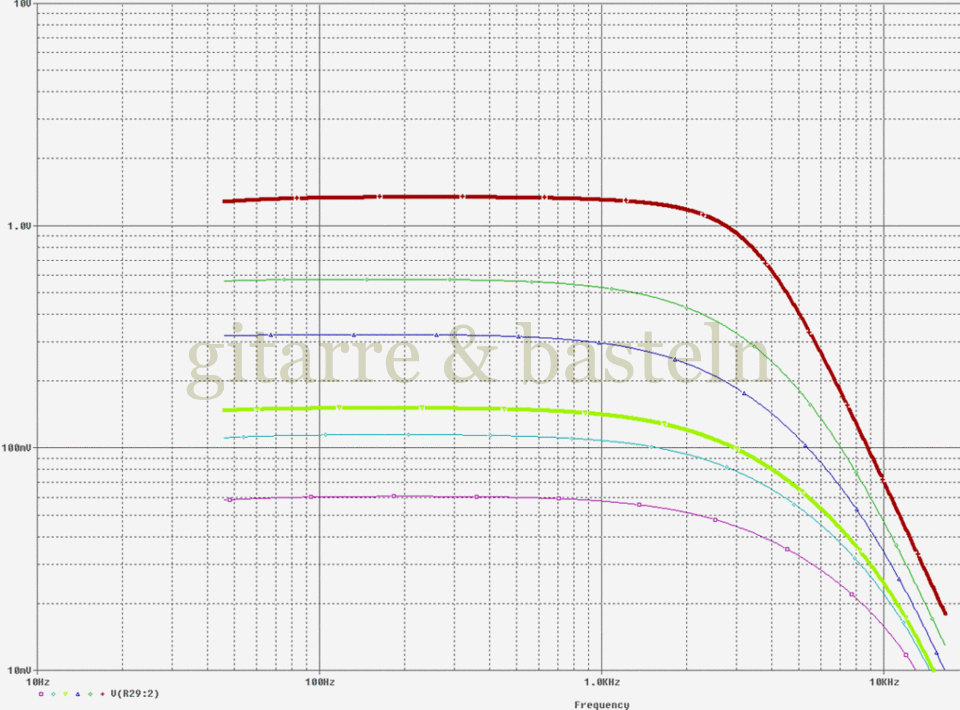
Abb. 2.17: Simulierter Frequenzgang von (mit Humbuckern bestückter) Gitarre und Eingangsschaltung eines Red Llama für verschiedene Einstellungen des Gitarrenvolumenreglers (Gitarrenton- und Gain-Regler jeweils 1)
Betrachtet man diesen Frequenzgang, dann scheint es so, dass das originale Red Llama für eine „Singlecoil-lastige“ Gitarre wie eine Stratocaster geeigneter ist – ein etwas kratziges wie dynamisches „Anzerren“, ein linearer Boost in die Eingangsstufe eines Verstärkers – dafür scheint das Red Llama in Zusammenhang mit hell, „drahtig“ und wenig basslastig klingenden Instrumenten sinnvoll. Eine Humbucker-bestückte Gitarre wie die „Les Paul“ läuft hier Gefahr, eher undynamisch und matschig zu klingen.
Literatur
- Manfred Zollner. Physik der Elektrogitarre (in einer älteren Ausgabe)
Kapitel 5 –Magnet-Tonabnehmer. Seite 108 ff.; Bezug über: gitec-forum.de
