Bass controls for Tele, Strat, and Les Paul—described by Jon Blackstone and discussed here: The theory: Telecaster—one wire is swapped; Stratocaster—a dual bass control and Les Paul—the bass control is switched. Finally, an one-handed radio knob.
Bass tone control for guitars
Kapitelinhalt:[ Skip ]- Theory, theory, theory •
- Telecaster—bass instead of treble controls •
- Stratocaster—two tone controls •
- Les Paul—switchable tone control •
- P. S: Les Paul—double tone control •
- Conclusion •
- Translation
Theory, theory, theory
Some time ago, the author found an article on Jon Blackstone's website entitled “Teach Your Neck Pickup to Twang”—about the possible use of a bass control for the neck pickup of a guitar (Telecaster, Stratocaster, Les Paul) to achieve a sound typical of the 1950s.
These suggestions will be discussed below. To this end, the circuits will be redrawn as circuit diagrams (not as wiring diagrams), counterproposals will be explained, and—for a simplified circuit—the so-called −3dB-frequencies, and the maximum attenuation will be calculated.
The highly simplified bass control circuit is shown in the following Figure 6.1—on the left abstracted for calculation and on the right in the application suggested by Jon Blackstone:

Fig. 6.1: Circuit principle for a bass control in a guitar—left: general principle for deriving frequencies; right: circuit with several existing resistors.
The circuits can therefore be abstracted to the basic circuit shown in Figure 6.1 on the left and its frequency response to the following equation 6.1:
\( \begin{eqnarray} \frac{u_{\textrm{Out}}}{u_{\textrm{In}}} & = & \frac{R_{2} } {R_{2} + (R_{1}\,||\,X_{C1}) } \\~\\ & = & \frac{R_{2} } {R_{2} + \cfrac {R_{1} \cdot{} X_{C1}} {R_{1} + X_{C1}} } \\~\\ & = & \frac{R_{2} } {R_{2} + \cfrac {R_{1} \cdot{} \cfrac{1}{ȷωC_{1}}} {R_{1} + \cfrac{1}{ȷωC_{1}}} } \\~\\ & = & \frac{R_{2} } {R_{2} + \cfrac {R_{1}} {R_{1} \cdot{} ȷωC_{1} + 1} } \\~\\ & = & \frac{R_{2} \cdot{}\! \left( R_{1} \cdot{} ȷωC_{1} + 1 \right) } {R_{2} \cdot{}\! \left( R_{1} \cdot{} ȷωC_{1} + 1 \right) + R_{1} } \\~\\ & = & \frac{ R_{1}R_{2} \cdot{} ȷωC_{1} + R_{2} } { R_{1}R_{2} \cdot{} ȷωC_{1} + R_{1} + R_{2} } \\~\\ & = & \frac{R_2} {R_1 + R_2} \cdot{}\! \frac{ R_{1} \cdot{} ȷωC_{1} + 1 } {\cfrac{R_{1}\cdot{R_{2}}} { R_{1} + R_{2} } \cdot{} ȷωC_{1} + 1 } \\~\\ \frac{u_{\textrm{Out}}}{u_{\textrm{In}}} & = & \frac{R_2} {R_1 + R_2} \cdot{}\! \frac{ ȷωC_{1}R_{1} + 1 } { ȷωC_{1} \left( R_{1}\,||\,R_{2} \right) + 1 } \tag{6.1}\end{eqnarray} \)
This equation results in two −3dB frequencies—f1 and f2:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{1}\cdot{}R_{1} } \\~\\ f_2 & = & \frac{1} { 2π\cdot{}C_{1}\cdot{}\! \left( R_{1}\,||\,R_{2} \right) } \tag{6.2}\end{eqnarray} \)
and a maximum damping Dmax:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{R_1} {R_1\,||\,R_2} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{R_1\cdot{}(R_1 + R_2)} {R_1\cdot{}R_2} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{R_1} {R_2} + 1 \right) \tag{6.3}\end{eqnarray} \)
There is therefore a maximum attenuation, especially for the low frequencies, which depends on the ratio of the two resistors R1 to R2 or on the ratio of the two −3dB frequencies f1 to f2. By changing the capacitor C1, both frequencies and the attenuation curve are shifted up or down without changing attenuation and attenuation curve.
With the circuit shown on the right in Figure 6.1, the situation becomes more complicated in that the lower and upper resistances change with the position of the bass control. For simplicity, we will assume maximum bass attenuation (the wiper of the bass control at the junction between Rbass and Rfoot).
In this case, the resistors Rfoot (perhaps 150 kΩ on a Stratocaster), Rtone (220 kΩ; Ctone is irrelevant when the tone control is fully turned up; the −3dB frequency of Rtone and Ctone is approximately 15 Hz), the volume control Rvol (220 kΩ), and the input resistance of the following stage (1 MΩ) form the lower resistor R2 at approximately 60 kΩ.
It should also be clear that the position of the tone control (if the tone control is placed after the bass control) also influences the maximum bass roll-off via the described parallel circuit—the further the tone control is turned back “behind” the bass control, the greater the maximum bass roll-off.
So much for the theory, now for the suggestions for the individual guitars:
Telecaster—bass instead of treble controls
First, the circuit proposed by Jon Blackstone for the Telecaster—for copyright reasons and for clarity, this is a circuit diagram (not a wiring diagram), created by the author:
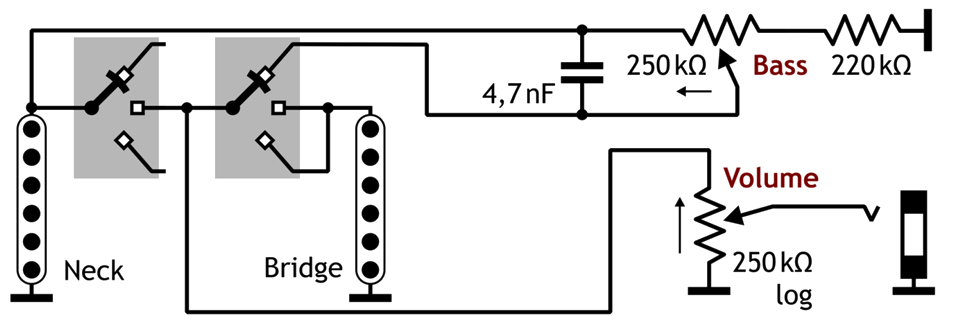
Fig. 6.2: Circuit proposal by Jon Blackstone for an adjustable bass cutout in a Telecaster (switch in the neck pickup position).
You can see that when the switch is in the middle position, the pickups are still loaded by the bass control circuit, which could potentially adversely affect the treble response.
It may work better to connect the cable from neck pickup not directly the top of the bass control, but rather over the switch, as shown in the following Figure 6.3:
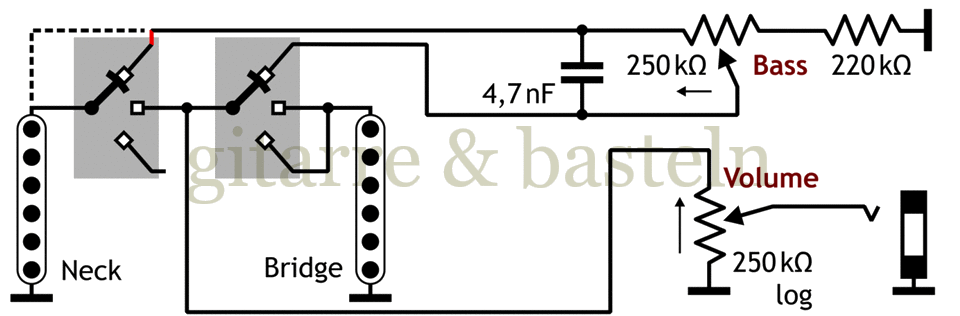
Fig. 6.3: Circuit proposal by Jon Blackstone for an adjustable bass cutout in a Telecaster with a suggested modification by the author—the red connection instead of the dashed line (switch set to neck pickup position).
Now about something math, sound and frequencies:
The two −3dB frequencies for the frequency response of the bass cutoff in a circuit according to Figure 6.3 are:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1} {2π\cdot{} 0{,}0047\,\textrm{μF}\cdot{} 0{,}25\,\textrm{MΩ} } \\~\\ & = & \frac{1} {2π\cdot{} 0{,}0047\cdot{}0{,}25 } \cdot{}\! \frac{1} {10^{-6}\cdot{} 10^{6}} \cdot{}\! \frac{\mathrm{V}\cdot{} \mathrm{A} } {\mathrm{As}\cdot{} \mathrm{V} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}25 } \\~\\ f_1 & \approx{} & 135\,\textrm{Hz} \tag{6.4}\end{eqnarray} \)
For f2, the conversion from 1/microfarads and 1/megaohms to Hertz is skipped here:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Fuß}\,||\,R_{Vol} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}\! \left( 0{,}25\,||\,0{,}22\,||\,0{,}25 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}08 } \\~\\ f_2 & \approx{} & 420\,\textrm{Hz} \tag{6.5}\end{eqnarray} \)
The maximum bass roll-off can be derived as follows:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{420\,\textrm{Hz}} {135\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 10\,\textrm{dB} \tag{6.6}\end{eqnarray} \)
Stratocaster—two tone controls
Jon Blackstone's website also provides a circuit suggestion for the Stratocaster—one of the two tone controls becomes the bass control for the individual neck pickup, the other the general tone control (treble cut):
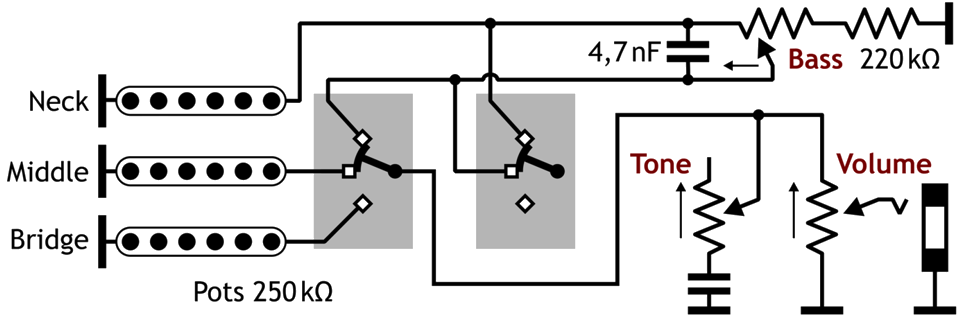
Fig. 6.4: Jon Blackstone's website also provides a circuit suggestion for the Stratocaster—one of the two tone controls becomes the bass control for the individual neck pickup, the other the general tone control (treble cut):
The frequency response of the circuit changes slightly due to the fact that there is a tone control after the bass control. So, first, we do the calculations. The lowest lower −3dB frequency remains the same:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}25 } \\~\\ f_1 & \approx{} & 135\,\textrm{Hz} \tag{6.7}\end{eqnarray} \)
By connecting the tone control after the bass control, the lower resistance, the total resistance of the parallel circuit decreases, and the upper −3dB frequency increases:
\( \begin{eqnarray} f_2 & = & \frac{1}{2π\cdot{} C_{Bass}}\cdot{} \\&& \frac{1} { \left( R_{Bass}\,||\,R_{Fuss}\,||\,R_{Ton}\,||\,R_{Vol}\,||\,R_{Ein} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047}\cdot{} \\&& \frac{1} {\left( 0{,}25\,||\,0{,}22\,||\,0{,}25\,||\,0{,}25 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}059 } \\~\\ f_2 & \approx{} & 570\,\textrm{Hz} \tag{6.8}\end{eqnarray} \)
Increasing f2 also increases the maximum bass roll-off:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{570\,\textrm{Hz}} {135\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 13\,\textrm{dB} \tag{6.9}\end{eqnarray} \)
However, there are two minor disadvantages:
-
On the one hand, the bass control also puts a strain on the pickups and their treble reproduction in the intermediate position between the neck and midrange pickups.
-
Secondly, the tone control could influence the bass control, as it is located after the bass control.
For this reason, a special circuit is proposed with a higher resistance bass control potentiometer (and without a foot resistor). Additionally, the proposal uses a rather specialized “MN” potentiometer from Bourns to realize a double low cut control—either for the neck pickup only, either for all pickups.
Description MN potentiometer:
This MN-potentiometer (more precisely, the “Bourns® Model PDB182-GTRB Blend-Balance Guitar Potentiometer”—see this PDF for documentation, available—at least in europe—from german webshop musikding.de) is actually used to mix the signals from two pickups—i.e., turning it from center to the left turns down the first pickup (and doesn't change the second at all), while turning it from center to the right doesn't change the first pickup at all (and turns down the second).
The following Figure 6.5—a facsimile from the manufacturer's information—shows the behavior of the MN potentiometer in a diagram.

Fig. 6.5: Control characteristics of an MN potentiometer—facsimile from the manufacturer's information.
This means that one of the two individual potentiometers of the tandem potentiometer only works “left of center”, and the other only “right of center.”
So this potentiometer allows for a ”double“ bass control—either—turned from center to left—a bass control for the neck pickup alone, or—turned from center to right—a bass control for all pickup combinations. The bass control for the neck pickup is short-circuited by the 5-position switch in all other pickup combinations.
The treble control for all pickups is placed before the bass control, making it more difficult to influence it.
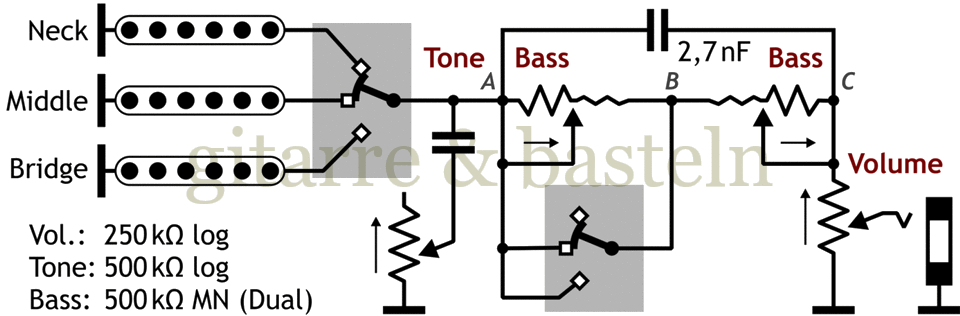
Fig. 6.6: Circuit proposal with an adjustable low cut for the neck pickup or all pickups in a Stratocaster using an MN potentiometer (switch set to the neck and middle pickup position).
The frequency response's simulation of the proposed circuit could be seen in Figure 6.7 below—the input resistance of 1 MΩ refers to the input impedance of the downstream amplifier, and the bass control of 480 kΩ refers to the MN potentiometer (as measured):

Fig. 6.7: Frequency responses for a double bass filter in a Stratocaster guitar—circuit according to Figure 6.6.
The corresponding derivation is also shown. The capacitor is reduced from 4.7 nF to 2.7 nF to achieve a similar lower frequency of −3dB with the larger bass control:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}0{,}48 } \\~\\ f_1 & \approx{} & 120\,\textrm{Hz} \tag{6.10}\end{eqnarray} \)
However, f2 is still slightly smaller:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}% \left(% R_{Bass}\,||\,R_{Vol}\,||\,R_{In} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}\! \left( 0{,}48\,||\,0{,}25 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}0{,}14 } \\~\\ f_2 & \approx{} & 420\,\textrm{Hz} \tag{6.11}\end{eqnarray} \)
which also results in lower bass attenuation:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{420\,\textrm{Hz}} {120\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 11\,\textrm{dB} \tag{6.12}\end{eqnarray} \)
The possible maximum bass attenuation is approximately 11 dB. Ultimately, the lack of the additional foot resistor leads to a smaller value of f2 and a lower maximum bass attenuation.
Two disadvantages of the proposed circuit should not be ignored—there is no additional foot resistor for the bass voltage divider, and the series resistor is relatively small. The former makes the circuit relatively sensitive to the effect of a lower input impedance in the first downstream effects device or amplifier, while the latter limits the possible maximum attenuation.
The first problem can be circumvented by using a fixed first downstream device with a high input impedance—an input buffer on the pedalboard, tuner, etc. could help. The second problem (the insufficient maximum series resistance) could be solved with a 1 MΩ MN potentiometer—this would offer a wider range of control; the author could not find one at musikding.de. However, a larger value for the MN potentiometer might require a smaller value for the capacitor.
A compromise could be to place the tone control between the two individual potentiometers of the MN potentiometer—for the neck pickup, the bass control is placed before the tone control (greater bass reduction, tone control affects the bass control), and for all pickups, it is placed after it (less bass reduction, tone control does not affect the bass control):
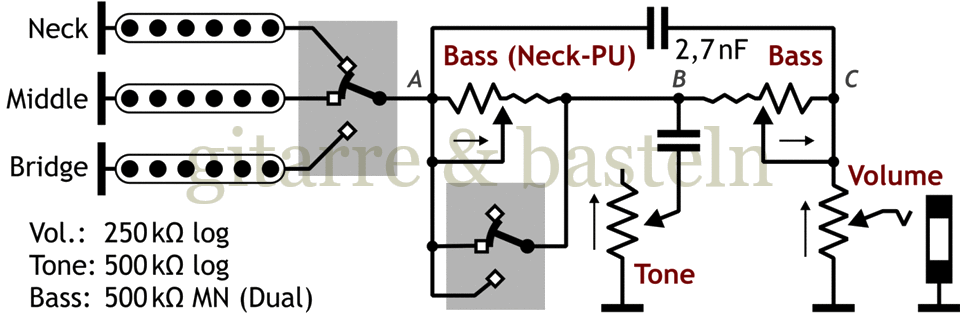
Fig. 6.8: Modification of the circuit proposal in Figure 6.6 for an adjustable bass cutout—the bass control is placed before the tone control for the neck pickup (slightly larger control range, but possible interactions between the two controls).
With this circuit trick, the upper −3dB frequency for the neck pickup and thus the maximum bass attenuation can be increased:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Treble}\,||\,R_{Vol}\,||\,R_{In} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}\! \left( 0{,}48\,||\,0{,}48\,||\,0{,}25 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}0{,}11 } \\~\\ f_2 & \approx{} & 540\,\textrm{Hz} \tag{6.13}\end{eqnarray} \)
The maximum bass attenuation is now:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{540\,\textrm{Hz}} {120\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 13\,\textrm{dB} \tag{6.14}\end{eqnarray} \)
Independently of this, the capacitor above the bass control could also be “split”—once between points A and B for the bass control of the neck pickup or once between points B and C for the bass control of all pickups, which opens up the possibility of adjusting the size of both capacitors to suit the sound.
Les Paul—switchable tone control
The bass control for the Les Paul's neck pickup is practical, but there may be applications where a treble cut is needed even there (extremely sophisticated jazz?, King Crimson solos?). Therefore, this control should also be switchable.
First, in Figure 6.9, Jon Blackstone's circuit proposal—again in a circuit diagram instead of a wiring diagram:

Fig. 6.9: Circuit proposal by Jon Blackstone for an adjustable bass cut in a Les Paul.
Following this, in Figure 6.10, is the circuit diagram with the switchable control—a standard push-pull potentiometer with a double-pole switch is sufficient here:
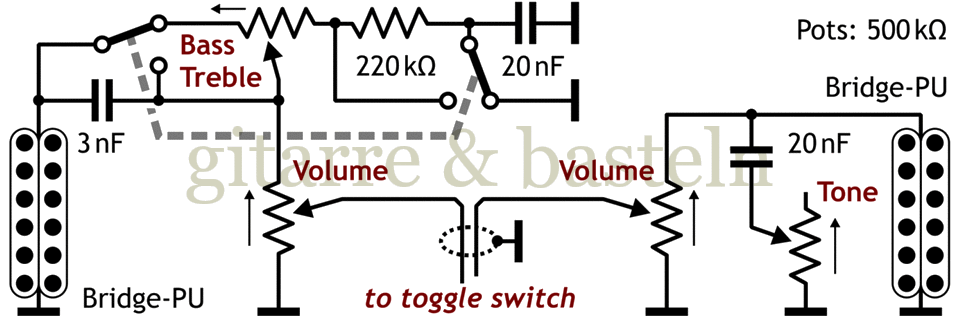
Fig. 6.10: Circuit proposal for a switchable bass/treble control for the neck pickup of a Les Paul (switch set to bass control position).
The disadvantage of this circuit, however, is that the potentiometer probably has a logarithmic characteristic, which is somewhat unfavorable for the bass control.
But there's always something …
Now, a brief mathematical background; we start with the formula for f1:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}48 } \\~\\ f_1 & \approx{} & 110\,\textrm{Hz} \tag{6.15}\end{eqnarray} \)
Compared to the Telecaster and Stratocaster circuits, f1 is slightly smaller here because the higher resistance of the bass potentiometer (250 kΩ vs. 480 kΩ) is not fully offset by the reduction of the parallel capacitor (4.7 nF vs. 3 nF). The same applies to f2:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Fuss}\,||\,R_{Vol}\,||\,R_{In} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}\! \left( 0{,}48\,||\,0{,}22\,||\,0{,}48\,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}10 } \\~\\ f_2 & \approx{} & 510\,\textrm{Hz} \tag{6.16}\end{eqnarray} \)
Overall, the maximum bass damping is comparably large:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{510\,\textrm{Hz}} {110\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 13\,\textrm{dB} \tag{6.17}\end{eqnarray} \)
At least this circuit idea has been implemented in practice—in the author's “Epiphone Paula” (see here; in german language).
P. S: Les Paul—double tone control
The best ideas often come too late—for example, the idea of a linear two-way tone control for the neck pickup of a Les Paul using a MN potentiometer (see Figure 6.11 below) just appeared after the author had rewired his Epiphone with a push-pull potentiometer for a combined tone control.
Nevertheless, here is the more recent idea:

Fig. 6.11: Circuit diagram for a bass and treble control in a Les Paul—from muffled (left) to neutral (center) to bass roll-off (right).
The tone control moves (as in very old radios) from muffled to thin, with the center setting corresponding to a fully turned-up classic tone control.
Now, again, to the mathematical part of the discussion—before deriving the maximum bass roll-off, first consider the two frequencies f1 and f2. For f1, here's no change—with the same potentiometer value and the same capacitor:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}48 } \\~\\ f_1 & \approx{} & 110\,\textrm{Hz} \tag{6.18}\end{eqnarray} \)
f2 is slightly smaller,
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass} } \cdot{} \\&& \frac{1} { \left( R_{Bass}\,||\,R_{Treble}\,||\,R_{Vol}\,||\,R_{In} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}\! \left( 0{,}48\,||\,0{,}48\,||\,0{,}5 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}14 } \\~\\ f_2 & \approx{} & 380\,\textrm{Hz} \tag{6.19}\end{eqnarray} \)
which also reduces the bass attenuation:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{380\,\textrm{Hz}} {110\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 11\,\textrm{dB} \tag{6.20}\end{eqnarray} \)
The possible maximum bass attenuation is approximately 11 dB. Ultimately, the lack of additional foot resistance results in a lower value of f2 and a lower maximum bass attenuation.
Conclusion
The circuits proposed by Jon Blackstone utilize a potentiometer with a “foot” resistor (between down / minimum connector and ground) and with a small capacitor between taper and upper / maximum connector. This arrangement allows for sufficiently large bass cuts, which, thanks to the foot resistor, are also somewhat protected against the influence of a smaller input impedance of a subsequent device.
Due to the lower foot resistor it is therefore not quite as likely that a connected stompbox with lower input impedance will be attributed a “lack of sound” like a “mid-range nose” here, because an input resistance significantly less than 1 MΩ shifts the upper −3dB frequency of the bass control significantly upwards.
The circuits suggested by the author, however, are intended to be used in a slightly more flexible manner—unless they are merely a suggested correction (for the Telecaster, see here) or a switch between bass control and treble control using a push-pull potentiometer (see here)—for example, as a combined bass-treble-control with a zero setting (see here), or a bass control for the Stratocaster—either for the neck pickup or for all pickups (see here).
So when using these circuits without foot resistor together with some lower input impedance vintage effects, the lowcut control's setting could be a chalange.
Translation
Article was written in (author's mother tongue) german language and afterwards translated to (something like) english language by the author using google translate.
